How to solve 30-60-90 triangles
Definition of a 30-60-90 triangles, including angles and side lengths
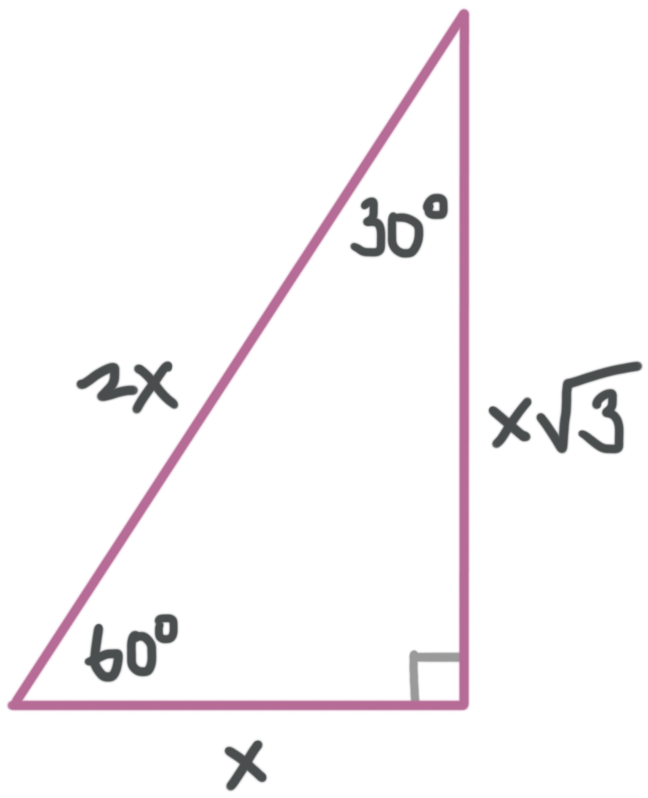
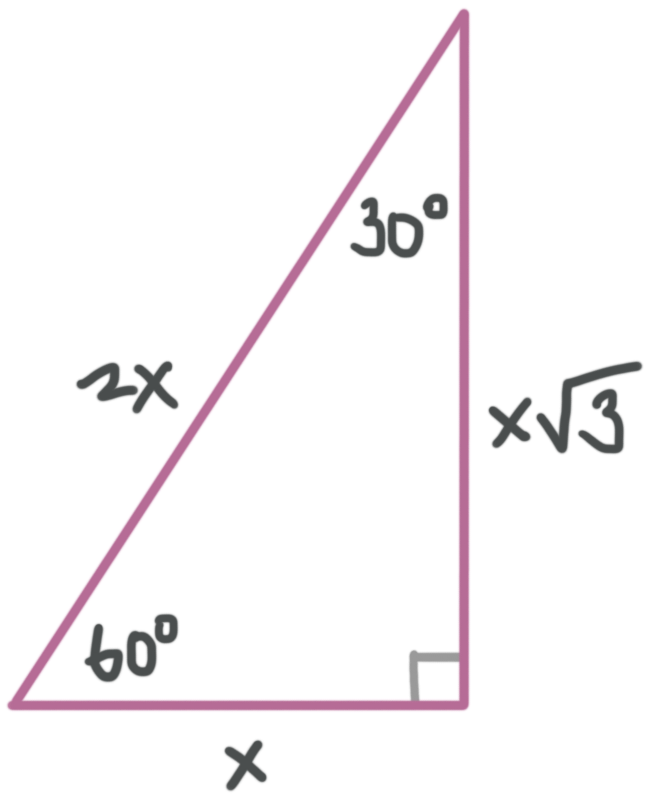
A ???30-60-90??? is a scalene triangle and each side has a different measure.
Since it’s a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
In this diagram, the short leg is ???x???, the long leg is ???x\sqrt{3}???, and the hypotenuse is ???2x???. These are always the ratios in a ???30-60-90??? triangle.
We can use the relationships in the diagram to solve all ???30-60-90??? triangles.
How to solve 30-60-90 triangles
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for the side lengths of a 30-60-90 triangle
Example
If ???x=6???, what is the length of the hypotenuse and the long leg?
The hypotenuse is related to ???x??? by ???2x???. We know ???x=6???, so the hypotenuse is ???2(6)=12??? units. The long leg is related to ???x??? by ???x\sqrt{3}???, so the long leg is ???6\sqrt{3}??? units.
Let’s look at another example.
Since it’s a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle.
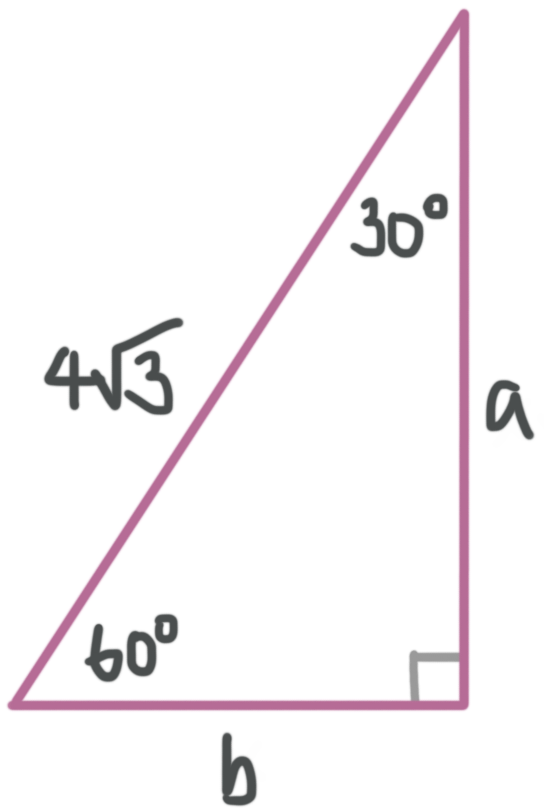
Example
What are the lengths of sides ???a??? and ???b????
The pattern for the sides of a ???30-60-90??? triangle is ???x??? for the short leg, ???x\sqrt{3}??? for the long leg, and ???2x??? for the hypotenuse. In this case we know the hypotenuse is ???4\sqrt{3}???, so
???2x=4\sqrt{3}???
???x=2\sqrt{3}???
The short leg ???b??? is ???2\sqrt{3}???. The long leg ???a??? is ???x\sqrt{3}???, or
???2\sqrt{3}\sqrt{3}=2(3)=6???
The long leg ???a??? is ???6??? units.
Let’s try another example.
Example
What are the lengths of the missing sides?
We know the long leg is ???5\sqrt{3}???, so
???x\sqrt{3}=5\sqrt{3}???
???x=5??? units
The short leg ???b??? is ???5??? units. Then the hypotenuse is
???2x=2(5)=10??? units
The hypotenuse ???c??? is ???10??? units.