Finding the area of a composite of rectangles using sums and differences
How do we find the area of composite figures?
In this lesson we’ll look at composite figures made from rectangles and how to find their areas.
A composite figure is made by combining different shapes. We’ll find the area of a composite figure by dividing the composite shape into shapes whose areas we already know how to find.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Area using a sum
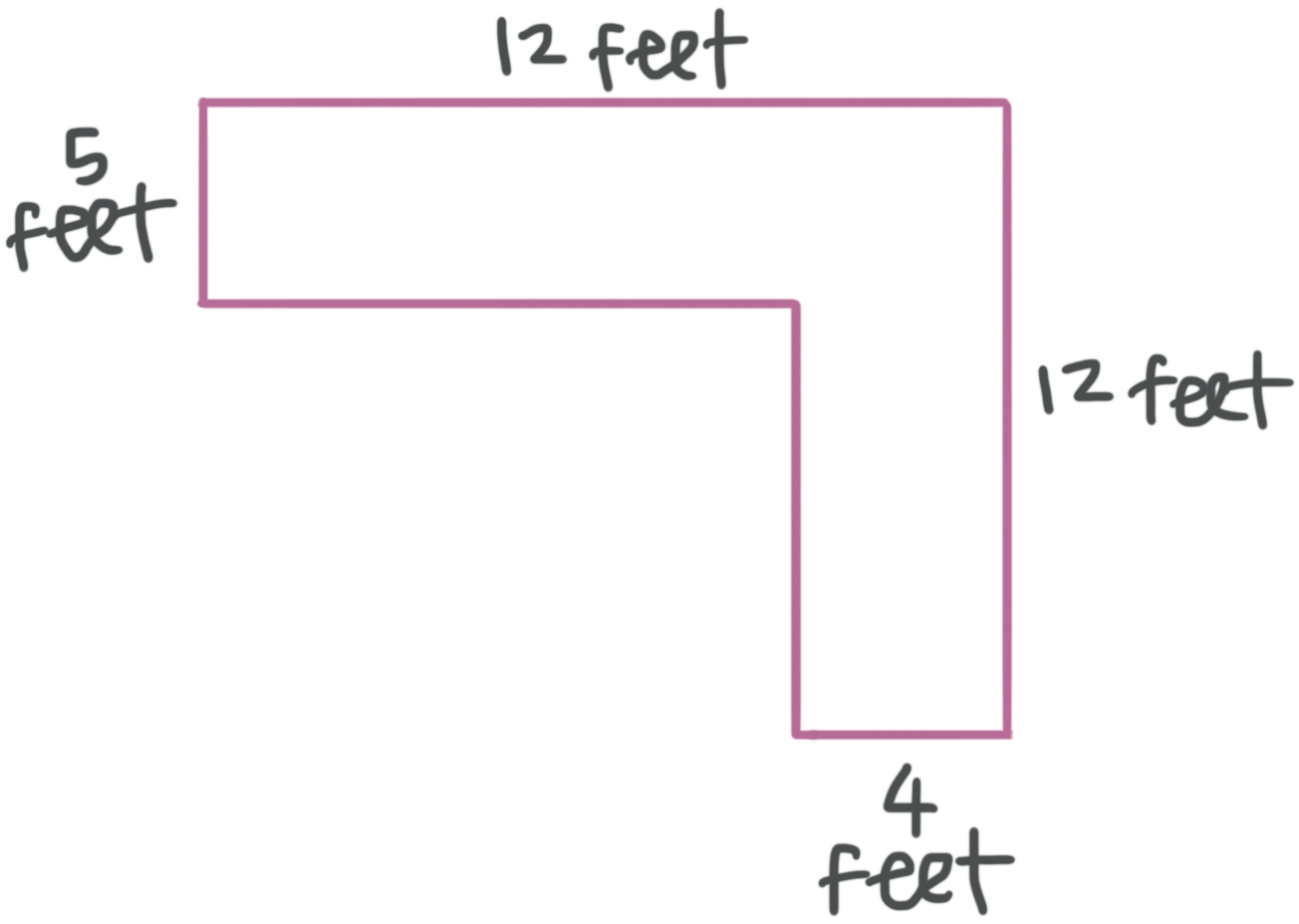
Let’s look at the composite figure below, which is made of rectangles. We can divide the shape into two rectangles, use the area formula for a rectangle twice to find their individual areas, and then add their areas to get the total area of the figure.
A shape can be divided in more than one way, but no matter how we divide the shape, the value of the area will always be the same. We can divide this figure into two rectangles with a horizontal line.
The height of the entire figure is ???12???, and the height of the upper rectangle is ???5???, so we can find the height of the lower rectangle by subtraction: ???12-5=7???. Now we know the dimensions of both of the smaller rectangles.
The dimensions of the upper rectangle are ???12??? and ???5???, so its area is
???A=bh???
???A=(12\text{ ft})(5\text{ ft})???
???A=60\ \text{ft}^2???
The dimensions of the lower rectangle are ???4??? and ???7???, so its area is
???A=bh???
???A=(4\text{ ft})(7\text{ ft})???
???A=28\ \text{ft}^2???
So the total area of the figure is
???A=60+28???
???A=88\ \text{ft}^2???
We could also divide this figure into two rectangles with a vertical line.
The length of the entire figure is ???12???, and the length of the right rectangle is ???4???, so we can find the length of the left rectangle by subtraction: ???12-4=8???. Now we know the dimensions of both rectangles.
The dimensions of the left rectangle are ???8??? and ???5???, so its area is
???A=lw???
???A=(8\text{ ft})(5\text{ ft})???
???A=40\ \text{ft}^2???
The dimensions of the right rectangle are ???4??? and ???12???, so its area is
???A=lw???
???A=(4\text{ ft})(12\text{ ft})???
???A=48\ \text{ft}^2???
So the total area of the figure is
???A=40+48???
???A=88\ \text{ft}^2???
Area using a difference
You can also use a difference to find the area of a composite figure. Let’s look at this one again.
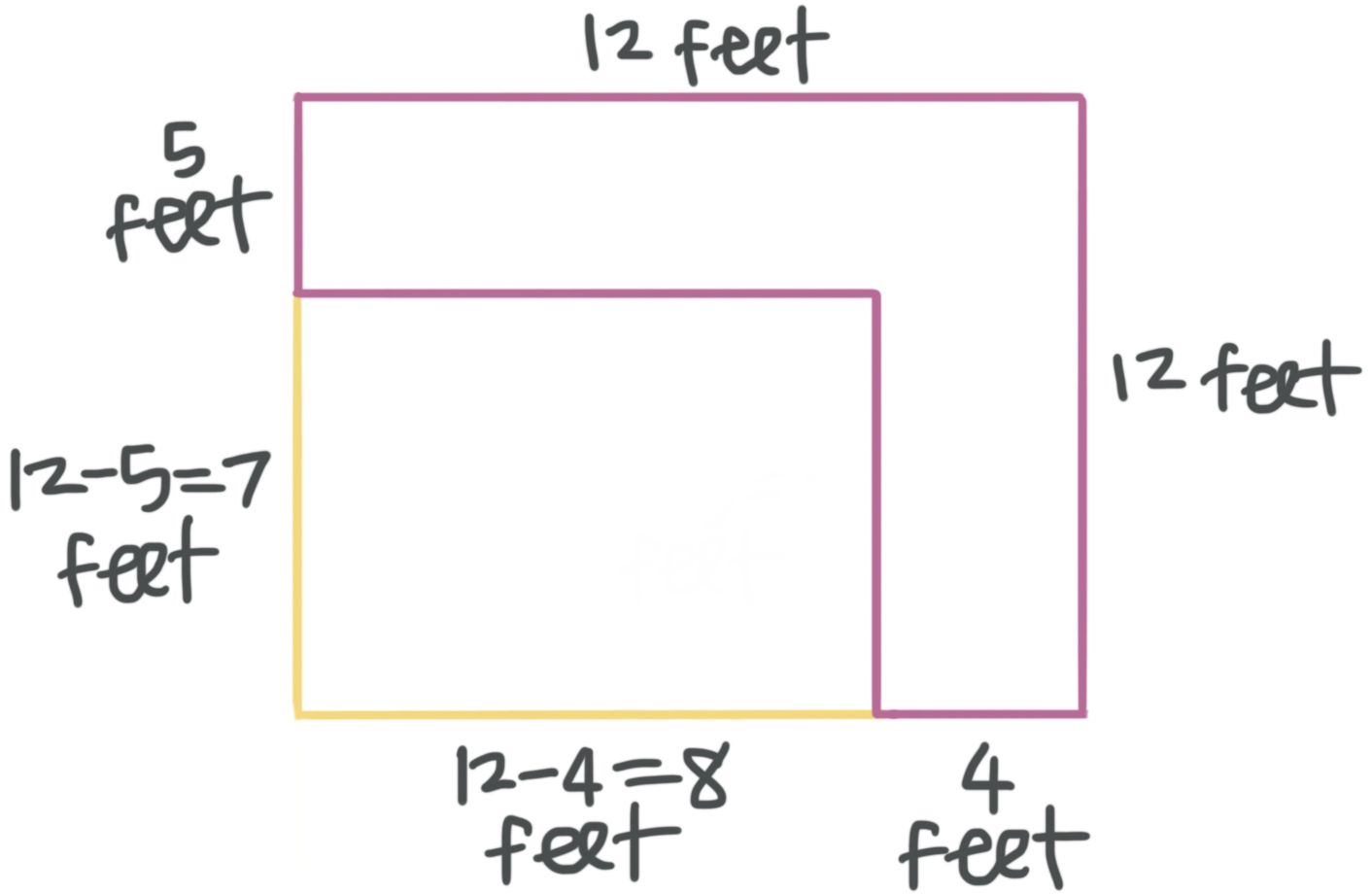
We can form a new, large rectangle by drawing a rectangle that fills in the empty space.
The base of the new, large rectangle we formed is ???12???, so the base of the rectangle we drew to fill in the empty space must be ???12-4=8???. The height of the new, large rectangle we formed is ???12???, so the height of the rectangle we drew to fill in the empty space must be ???12-5=7???.
The area of the new, large rectangle we formed (which is actually a square since its base is equal to its height) is ???12\cdot 12=144\ \text{ft}^2???. The area of the rectangle we drew to fill in the empty space is ???7\cdot 8=56\ \text{ft}^2???. So to find the area of the original figure, we can subtract the area of the rectangle we drew to fill in the empty space from the area of the new, large rectangle we formed:
???A=144-56=88\ \text{ft}^2???
Which is the same area we got when we used sums of areas of two rectangles instead of a difference of areas of two rectangles. Let’s do some more examples.
How to find the area of composite figures using sums and differences
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Finding the area of figures made by combining rectangles
Example
The figure is made by combining rectangles. What is the area of the figure?
The height of the lower rectangle is ???2???, so we can find the height of the upper rectangle by subtracting ???4-2=2??? cm. The dimensions of the upper rectangle are ???5??? by ???2???, so its area is
???A=bh???
???A=5\cdot 2???
???A=10\ \text{cm}^2???
We need to add to find the base of the lower rectangle. Its base is made of the horizontal ???6??? cm and the horizontal ???5??? cm. So the base of the lower rectangle is ???6+5=11??? cm. The dimensions of the lower rectangle are therefore ???2??? by ???11???, so its area is
???A=bh???
???A=2\cdot 11???
???A=22\ \text{cm}^2???
So the total area of the figure is
???A=10+22=32\ \text{cm}^2???
Let’s do one more example.
A shape can be divided in more than one way, but no matter how we divide the shape, the value of the area will always be the same.
Example
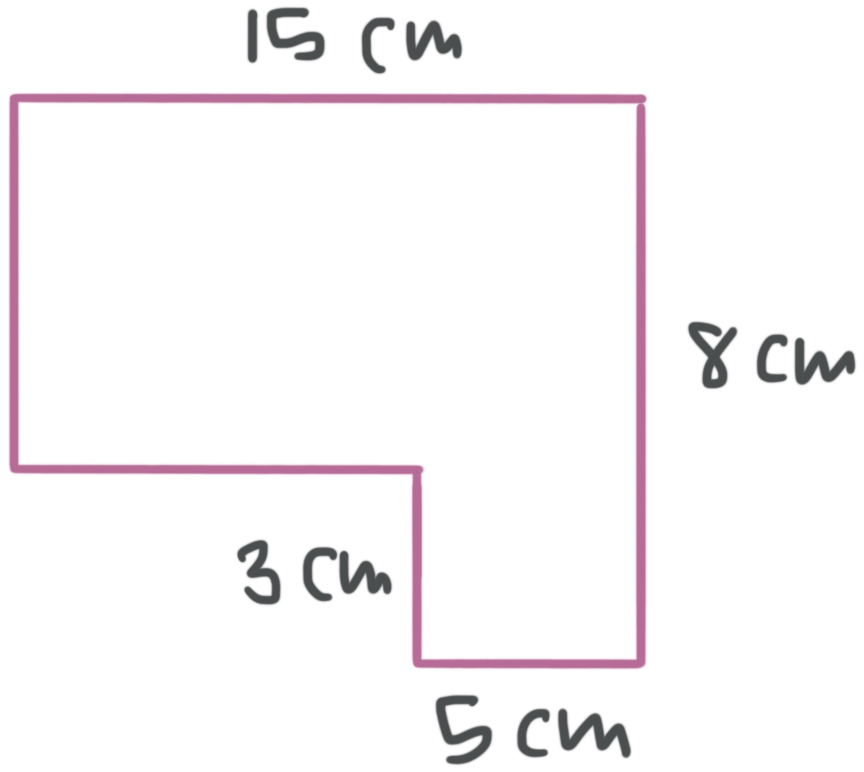
The figure is made by combining rectangles. What is the area of the figure?
Here’s one way to solve the problem: Draw the rectangle that fits in the empty space.
The height of the whole figure is ???8???, and the base of the whole figure is ???15???. The dimensions of the whole figure are ???15??? by ???8???, so its area is
???A=bh???
???A=15\cdot 8???
???A=120\ \text{cm}^2???
The empty space has a height of ???3???, and we can find the base by subtracting ???15-5=10??? cm. The dimensions of the empty space are therefore ???10??? by ???3???, so its area is
???A=bh???
???A=10\cdot 3???
???A=30\ \text{cm}^2???
We can then say that the area of the original figure is
???A=bh???
???A=120-30???
???A=90\ \text{cm}^2???