Finding average value from a double integral

Formula for average value with a double integral

We can estimate the average value of a region of level curves by using the formula

$f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}$

where $A(R)$ is the area of the rectangle defined by $R=[x_1,x_2]\times[y_1,y_2]$, and where the double integral gives the volume under the surface $f(x,y)$ over the region $R$.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

If an equation is not given, we can use the provided diagram to estimate the value of the function at the midpoints.

Finding average value over a specific region using a double integral with a multivariable function

---

Take the course

Want to learn more about Calculus 3? I have a step-by-step course for that. :)

---

Using level curves to estimate the average value over a region

Example

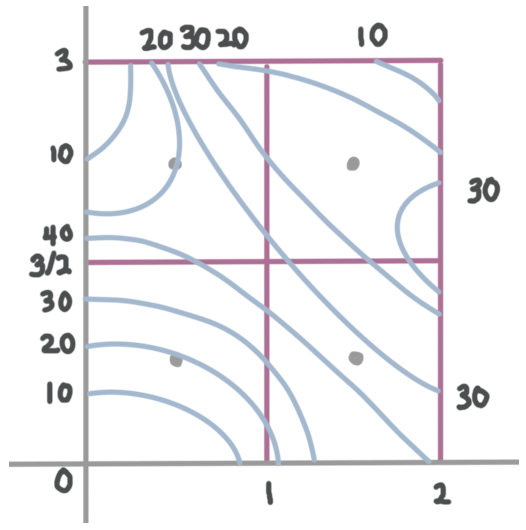
Use the sketch of level curves to estimate the region’s average value where $m=n=2$ and $R=[0,2]\times[0,3]$.

The question is asking us to use a sketch of the level curves that represent our function to estimate the average value of the region depicted and defined by $R=[0,2]\times[0,3]$. We’ll need to use the formula for average value:

$f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}$

We can start by solving for $A(R)$, the total area of the region $R$.

$A(R)=(2)(3)$

$A(R)=6$

Next, we can solve for $\Delta{A}$, which is the area of one of the subrectangles. Based on the figure we were given, the width of each subrectangle is $1$ and the height is $3/2$. Which means that the area of each subrectangle is

$\Delta{A}=(1)\left(\frac32\right)$

$\Delta{A}=\frac32$

If an equation is not given, we can use the provided diagram to estimate the value of the function at the midpoints.

Next we need the midpoints of each subrectangle.

Using $R=[0,2]\times[0,3]$, $m=n=2$ and our diagram, we can see that the midpoints of the four smaller rectangles are

$\left(\frac12,\frac34\right)$, $\left(\frac32,\frac34\right)$, $\left(\frac12,\frac94\right)$ and $\left(\frac32,\frac94\right)$

Since we don’t have an equation for our function, we can use the diagram of its level curves to estimate the functions values at each midpoint.

At $\left(\frac12,\frac34\right)$, the function is approximately $19$.

At $\left(\frac32,\frac34\right)$, the function is approximately $35$.

At $\left(\frac12,\frac94\right)$, the function is approximately $20$.

At $\left(\frac32,\frac94\right)$, the function is approximately $26$.

Now we have everything we need to find an estimate for the function’s average value over the region. We’ll use the formula

$f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}$

but since we don’t have the function, we’ll use the midpoint rule formula instead of the double integral, such that the formula becomes

$f_{ave}=\frac{1}{A(R)}\left[\Delta{A}\left(f(x_1,y_1)+f(x_2,y_2)+f(x_3,y_3)+f(x_4,y_4)\right)\right]$ 

$f_{ave}=\frac{1}{6}\left[\frac32\left(19+35+20+26\right)\right]$

$f_{ave}=\frac{1}{6}\left[\frac32\left(100\right)\right]$

$f_{ave}=\frac{300}{12}$

$f_{ave}=25$

Using midpoint rule, this is our estimate for the function’s average value over the region.

---

Get access to the complete Calculus 3 course

---