Probability with binomial random variables
Conditions of a binomial random variable
Remember that “bi” means two, so a binomial variable is a variable that can take on exactly two values. A coin is the most obvious example of a binomial variable because flipping the coin can only result in two values: heads or tails.
On the other hand, a ???6???-sided die doesn’t produce a binomial variable, since rolling the die can result in ???6??? possible outcomes, not ???2???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The two outcomes that the binomial random variable can take do not have to be equally probable. The probability of getting heads when I flip a fair coin is a binomial random variable where the probability of “success” is ???50\%???. But the probability of choosing a girl from my math class when I randomly choose one student might be a binomial random variable where the probability of “success” is ???70\%??? (if ???70\%??? of the students in my class are female).
Binomial random variables
In order for a variable ???X??? to be a binomial random variable,
each trial must be independent,
each trial can be called a “success” or “failure,”
there are a fixed number of trials, and
the probability of success on each trial is constant.
Let’s think about ???X??? as how many heads we get when we flip a coin ???10??? times.
Each trial is independent, because the result of one flip doesn’t effect the result of any other flip.
Each trial can be called a success or failure because “heads” is a success and “tails” is a failure.
We’re flipping the coin ???10??? times, so there are a fixed number of trials.
The probability of getting heads on the first flip is ???50\%???, the probability of getting heads on the second flip is ???50\%???, the probability of getting heads on the third flip is ???50\%???, etc. The probability of heads in each trial is constant.
So if ???X??? is how many heads we get when we flip a coin ???10??? times, then we could call ???X??? a binomial random variable. On the other hand, let’s think about ???J??? as how many jacks we get when we pull ???3??? cards from a deck without replacing the card after each pull.
Each trial is not independent, because the result of the first pull effects the result of every pull thereafter. If we get a jack on the first pull, then the probability we get a jack on the second pull is ???3/51???. But if we get something other than a jack on the first pull, then the probability we get a jack on the second pull is ???4/51???.
Each trial can be called a success or failure because a jack is a success and anything else is a failure.
We’re pulling a card ???3??? times, so there are a fixed number of trials.
The probability of getting a jack on the first pull is ???4/52???. But the probability of getting a jack on the second pull changes depending on what we got on the first pull. The probability of pulling a jack in each trial is not constant.
Since it fails two of the four conditions, ???J??? cannot be called a binomial random variable.
Binomial probability
In binomial probability questions, we’re often asked to figure out the probability that we get an exact number of “successes,” assuming we perform a specific number of independent trials. The formula we’ll use for this is
???P(k\text{ successes in }n\text{ attempts})=\binom{n}{k}p^k(1-p)^{n-k}???
where the binomial coefficient
???\binom{n}{k}???
is the combination ???_nC_k???, ???p??? is the probability of a success, ???k??? is the exact number of times we want the success, and ???n??? is the total number of independent trials we’ll run.
How to calculate probabilities for binomial random variables
Take the course
Want to learn more about Probability & Statistics? I have a step-by-step course for that. :)
Pulling marbles from a bag can be modeled by a binomial random variable
Example
Let’s say there are three marbles in a bag: ???2??? are green and ???1??? is red. We’re going to do ???5??? trials where we pull a marble, note the color, and then replace the marble. What is the probability that we get the red marble exactly ???3??? times?
First, we’ll confirm that this is a binomial random variable.
Since we’re replacing each marble we pull before pulling another, each pull is an independent trial.
We can classify a red marble as a success, and green marble as a failure.
There are a fixed number of trials: ???5???.
The probability of success (getting a red marble) is constant through each trial, since we’re replacing the marbles. Since all four conditions are met, this is a binomial random variable.
We’re trying to pull a red marble exactly ???3??? times in ???5??? pulls. To solve this problem, we need to first figure out how many possible combinations we can do this in.
???_5C_3=\binom53=\frac{5!}{3!(5-3)!}???
???_5C_3=\binom53=\frac{5!}{3!2!}???
???_5C_3=\binom53=\frac{5\cdot4\cdot3\cdot2\cdot1}{3\cdot2\cdot1\cdot2\cdot1}???
???_5C_3=\binom53=\frac{5\cdot4}{2\cdot1}???
???_5C_3=\binom53=\frac{20}{2}???
???_5C_3=\binom53=10???
Then to find the probability that we get exactly ???3??? reds on ???5??? pulls, we say that ???p??? is the probability of pulling a red marble, and therefore that the probability of pulling ???3??? red marbles in ???5??? pulls is
???P(k\text{ successes in }n\text{ attempts})=\binom{n}{k}p^k(1-p)^{n-k}???
???P(3\text{ reds in }5\text{ pulls})=(10)\left(\frac13\right)^3\left(\frac23\right)^2???
???P(3\text{ reds in }5\text{ pulls})=\frac{40}{243}\approx16.5\%???
In other words, we have approximately a ???16.5\%??? chance of getting exactly ???3??? red marbles when we pull a random marble from this bag ???5??? times.
A coin is the most obvious example of a binomial variable because flipping the coin can only result in two values: heads or tails.
Probability distributions for binomial random variables
We can also create a probability distribution for binomial random variables. Using our example of pulling a marble ???5??? times, where we have a ???1/3??? probability of pulling a red marble and ???2/3??? probability of pulling a green marble on each pull, we could calculate the following probabilities.
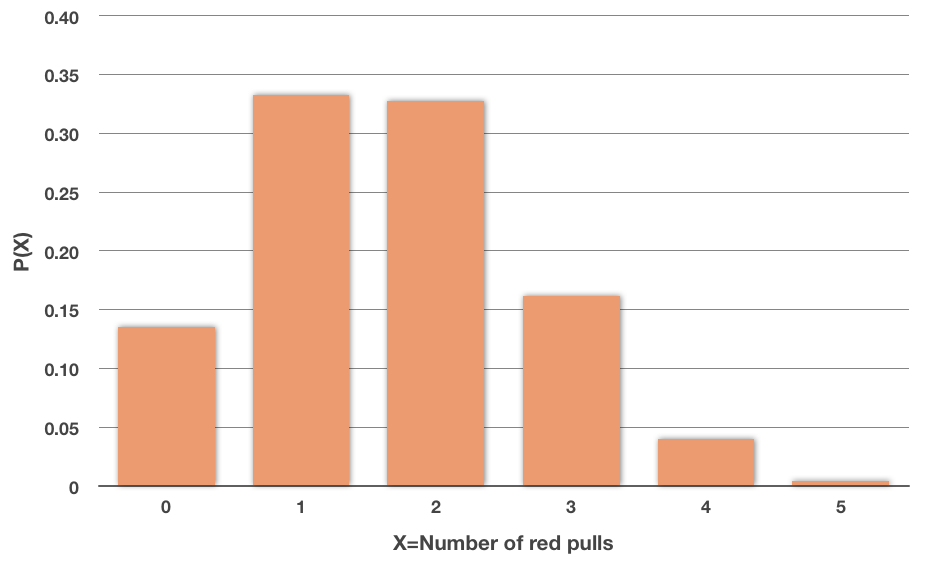
???P(0\text{ red in }5\text{ pulls})=\binom{5}{0}0.33^0 0.67^5=(1)(1)(0.67^5)\approx0.1350???
???P(1\text{ red in }5\text{ pulls})=\binom{5}{1}0.33^1 0.67^4=(5)(0.33^1)(0.67^4)\approx0.3325???
???P(2\text{ red in }5\text{ pulls})=\binom{5}{2}0.33^2 0.67^3=(10)(0.33^2)(0.67^3)\approx0.3275???
???P(3\text{ red in }5\text{ pulls})=\binom{5}{3}0.33^3 0.67^2=(10)(0.33^3)(0.67^2)\approx0.1613???
???P(4\text{ red in }5\text{ pulls})=\binom{5}{4}0.33^4 0.67^1=(5)(0.33^4)(0.67^1)\approx0.0397???
???P(5\text{ red in }5\text{ pulls})=\binom{5}{5}0.33^5 0.67^0=(1)(0.33^5)(0.67^0)\approx0.0039???
We could then plot this probability distribution to get a picture of the probability.
This probability distribution is a visual representation of the fact that we’re most likely to get ???1??? or ???2??? red marbles when we pull ???5??? times from the bag of marbles. We’re much less likely to get ???4??? or ???5??? red marbles when we pull ???5??? times.