Switching to a new coordinate basis

Changing the basis from xy-coordinates to a different coordinate plane

When we first learned to graph, we defined points in space using coordinates.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

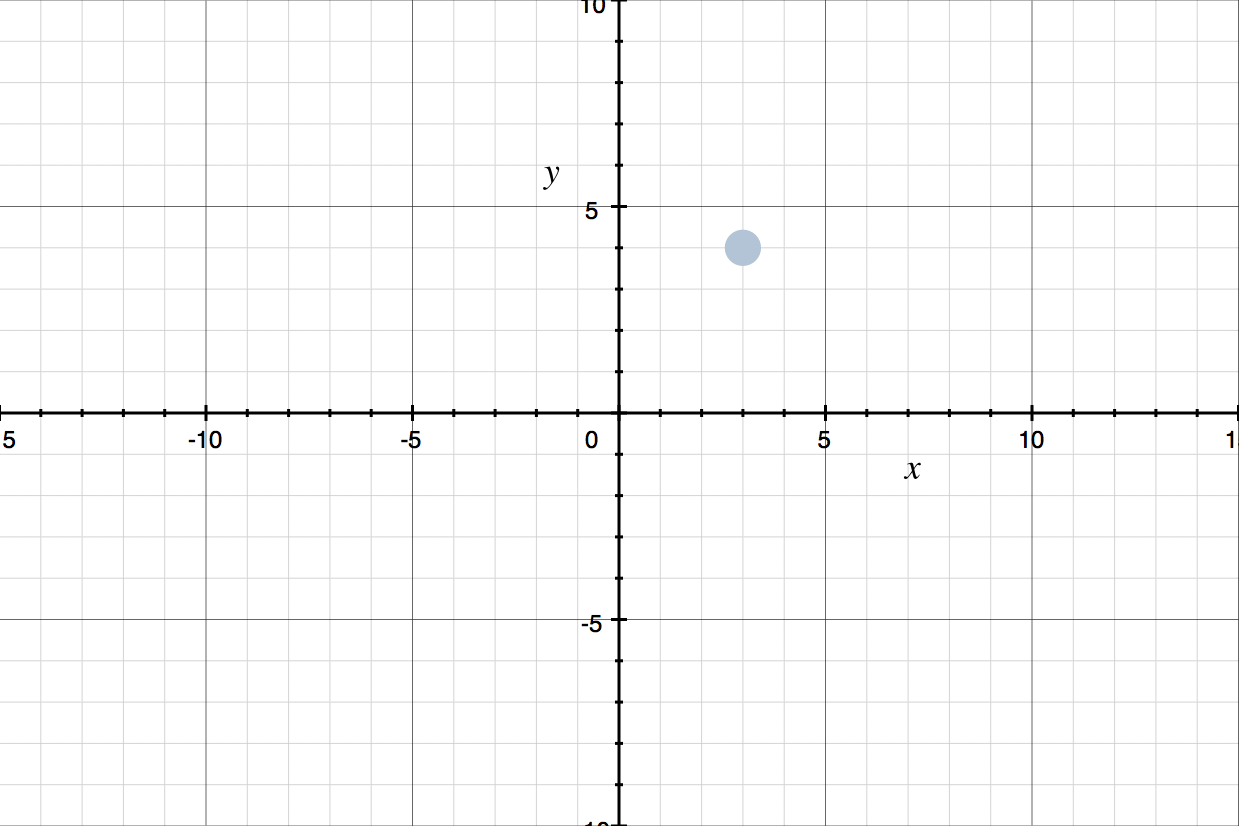
For instance, the point $(3,4)$ told us to move $3$ units from the origin horizontally toward the positive direction of the $x$-axis, and $4$ units vertically toward the positive direction of the $y$-axis.

We’ve also learned how to define the same point with vectors. The vector $\vec{v}=(3,4)$ will point us to the same point $(3,4)$. So the graph of $\vec{v}=(3,4)$ is

And we know that the same spot can be represented as a combination of the standard basis vectors $\bold{i}$ and $\bold{j}$. The vector $\bold{i}=(1,0)$ is the vector that points to $(1,0)$ and the vector $\bold{j}=(0,1)$ is the vector that points to $(0,1)$. So we can take $3$ of $\bold{i}$ and $4$ of $\bold{j}$ and again get to the same point. So the graph of $3\bold{i}+4\bold{j}$ is

In other words, up to now, plotting points has always been done using the standard basis vectors $\bold{i}$ and $\bold{j}$, or $\bold{i}$, $\bold{j}$, and $\bold{k}$ in three dimensions. Even when we were originally learning to plot $(3,4)$ back in an introductory Algebra class, and we knew nothing about vectors, we were really learning to plot $3\bold{i}+4\bold{j}$ in terms of the standard basis vectors, we just didn’t know it yet.

In this lesson, we want to see what it looks like to define points using different basis vectors. In other words, instead of using $\bold{i}=(1,0)$ and $\bold{j}=(0,1)$, can we use different vectors as the basis instead?

Changing the basis

Well, let’s say $V$ is a subspace of $\mathbb{R}^2$. And let’s say we wanted our basis vectors to be $\vec{v}=(2,1)$ and $\vec{w}=(1,3)$, such that $B=\{\vec{v},\vec{w}\}$ is basis for $\mathbb{R}^2$, and we want to figure out how to use these vectors to plot the same point we’ve been working with, $(3,4)$.

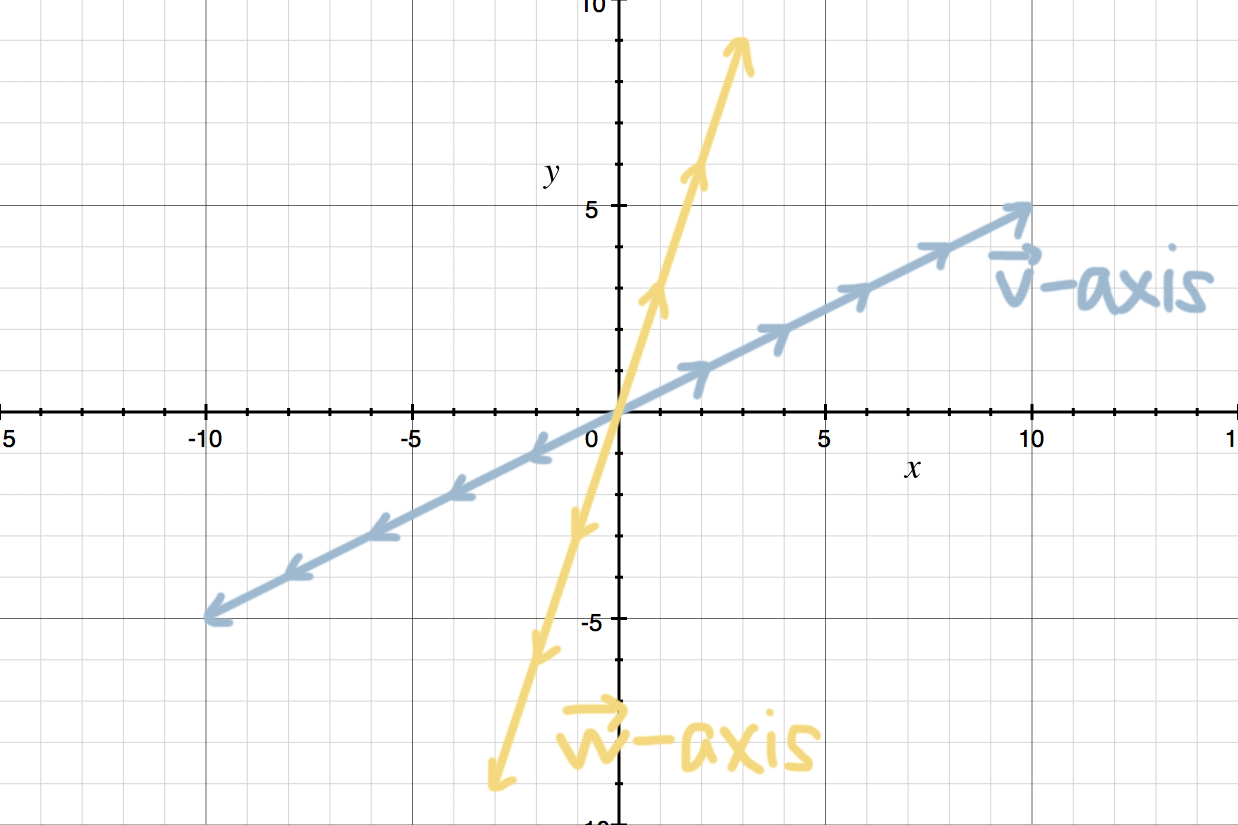
First, we could mark off a new set of axes. Realize that in the standard basis coordinate system, the perfectly horizontal $x$-axis is marked off in increments of $\bold{i}$, and the perfectly vertical $y$-axis is marked off in increments of $\bold{j}$.

Now we want to create a new set of axes, with one axis marked off in increments of $\vec{v}=(2,1)$, and the other axis marked off in increments of $\vec{w}=(1,3)$. Because $\vec{v}$ and $\vec{w}$ are not perfectly horizontal or vertical, the $\vec{v}$- and $\vec{w}$-axes won’t be perfectly horizontal or vertical either. Instead, the $\vec{v}$-axis will lie along $\vec{v}=(2,1)$, and the $\vec{w}$-axis will lie along $\vec{w}=(1,3)$.

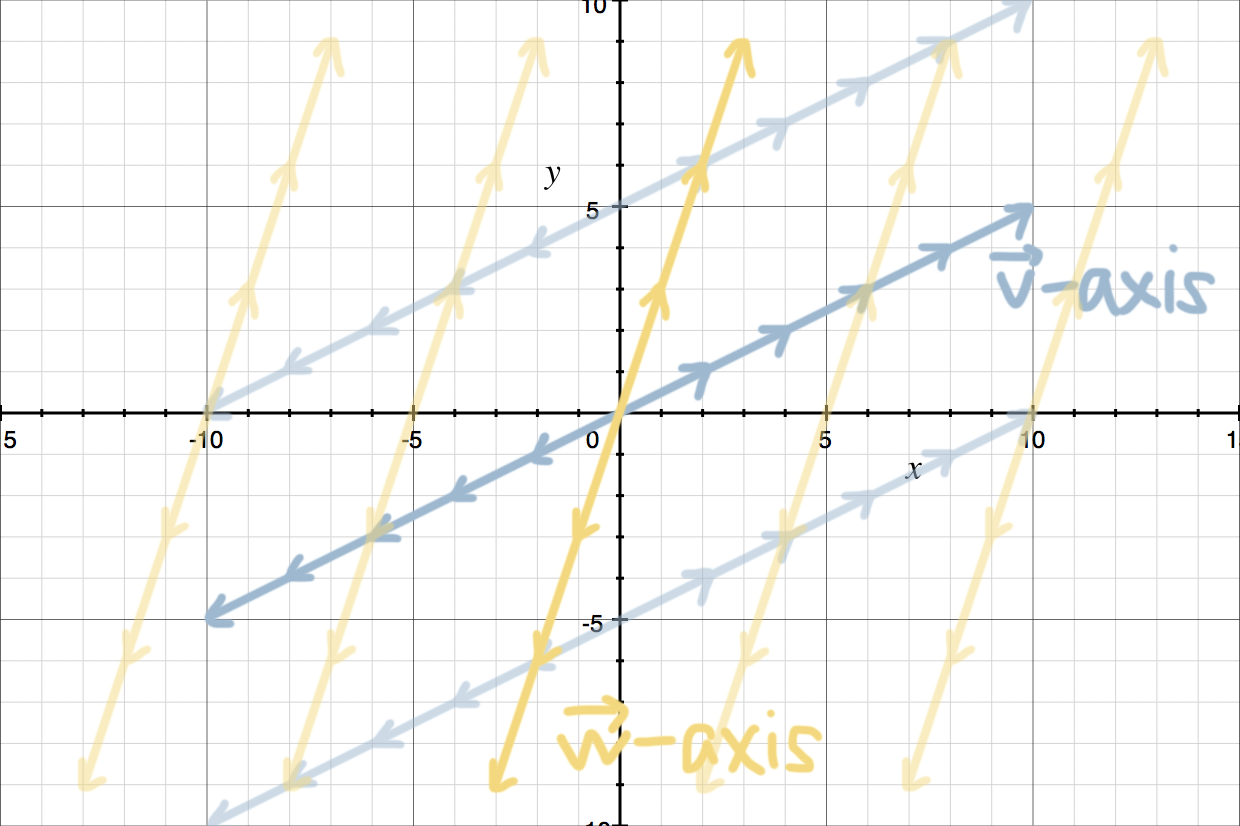
With the new axes sketched in, notice how we’ve marked them off in increments of $\vec{v}=(2,1)$ and $\vec{w}=(1,3)$, such that we can count how many $\vec{v}$s we’re moving out along the $\vec{v}$-axis, and how many $\vec{w}$s we’re moving out along the $\vec{w}$-axis.

Now we could sketch in a grid pattern that shows the whole “$\vec{v}\vec{w}$ coordinate system.”

Now to reach $(3,4)$, we can see that we need $1$ of $\vec{v}$ and $1$ of $\vec{w}$. We can either go out one unit of $\vec{v}$ toward the positive direction of the $\vec{v}$-axis, and then move one unit of $\vec{w}$ toward the positive direction of the $\vec{w}$-axis, or we can go the opposite way, moving out one unit of $\vec{w}$ toward the positive direction of the $\vec{w}$-axis and then one unit of $\vec{v}$ toward the positive direction of the $\vec{v}$-axis. Either way, we end up at $(3,4)$.

So the vector $\vec{x}\in V$ can be expressed uniquely as $\vec{x}=\vec{v}+\vec{w}$, and the coordinate vector of $\vec{x}$ in the basis $B$ is

$[\vec{x}]_B=\begin{bmatrix}1\\ 1\end{bmatrix}$

Change of basis matrix

So now that we understand the concept of changing from the standard basis vectors $\bold{i}$ and $\bold{j}$ to another set of basis vectors, like $\vec{v}$ and $\vec{w}$, let’s talk about how we’d actually go about doing that.

If we have the vectors that form the basis for the subspace, then we can use them to create a transformation matrix, called the change of basis matrix, that will change a vector from one basis to another.

For instance, earlier we changed from $\bold{i}=(1,0)$ and $\bold{j}=(0,1)$ to $\vec{v}=(2,1)$ and $\vec{w}=(1,3)$. Let’s say that $\vec{v}$ and $\vec{w}$ form the basis for the subspace $V$, $B=\{\vec{v},\vec{w}\}$, and some vector $\vec{x}$ can be expressed uniquely as $\vec{x}=c_1\vec{v}+c_2\vec{w}$. Then

$[\vec{x}]_B=\begin{bmatrix}c_1\\ c_2\end{bmatrix}$

are the coordinates of $\vec{x}$ relative to the basis $B$. We can then set up an equation in the form $A[\vec{x}]_B=\vec{x}$, where $A$ is the transformation matrix (the change of basis matrix from the standard basis to the basis $B$), and $[\vec{x}]_B$ is the vector $\vec{x}$ represented in terms of the basis $B$.

So if we want to know how the vector $\vec{x}=(3,4)$ will be represented by the new basis given by $\vec{v}=(2,1)$ and $\vec{w}=(1,3)$, then we plug into the equation.

$A[\vec{x}]_B=\vec{x}$

To figure out how $\vec{x}=(3,4)$ would be represented in $V$, we’ll solve the augmented matrix given by this equation.

This tells us that the solution to the equation is $[\vec{x}]_B=(1,1)$, or

In other words, if we want to represent $\vec{x}=(3,4)$ in terms of the standard basis vectors $\bold{i}=(1,0)$ and $\bold{j}=(0,1)$, then we need $3\bold{i}+4\bold{j}$. But if we want to represent $\vec{x}=(3,4)$ in terms of the alternate basis $\vec{v}=(2,1)$ and $\vec{w}=(1,3)$, then we need $1\vec{v}+1\vec{w}$, or just $\vec{v}+\vec{w}$. Which matches what we already found earlier when we sketched $(3,4)$ in the alternate basis.

And you can convert the other way, too. If you know you need $1\vec{v}+1\vec{w}$ to get to $(3,4)$ in the alternate basis, you can do the matrix multiplication to find out the right combination of $\bold{i}$ and $\bold{j}$ in the standard basis.

$A[\vec{x}]_V=\vec{x}$

$\begin{bmatrix}2(1)+1(1)\\ 1(1)+3(1)\end{bmatrix}=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$

$\begin{bmatrix}2+1\\ 1+3\end{bmatrix}=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$

$\begin{bmatrix}3\\ 4\end{bmatrix}=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$

How to create a change of basis matrix to change from xy-coordinates into a more convenient basis

---

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

---

Finding the combination of basis vectors

Example

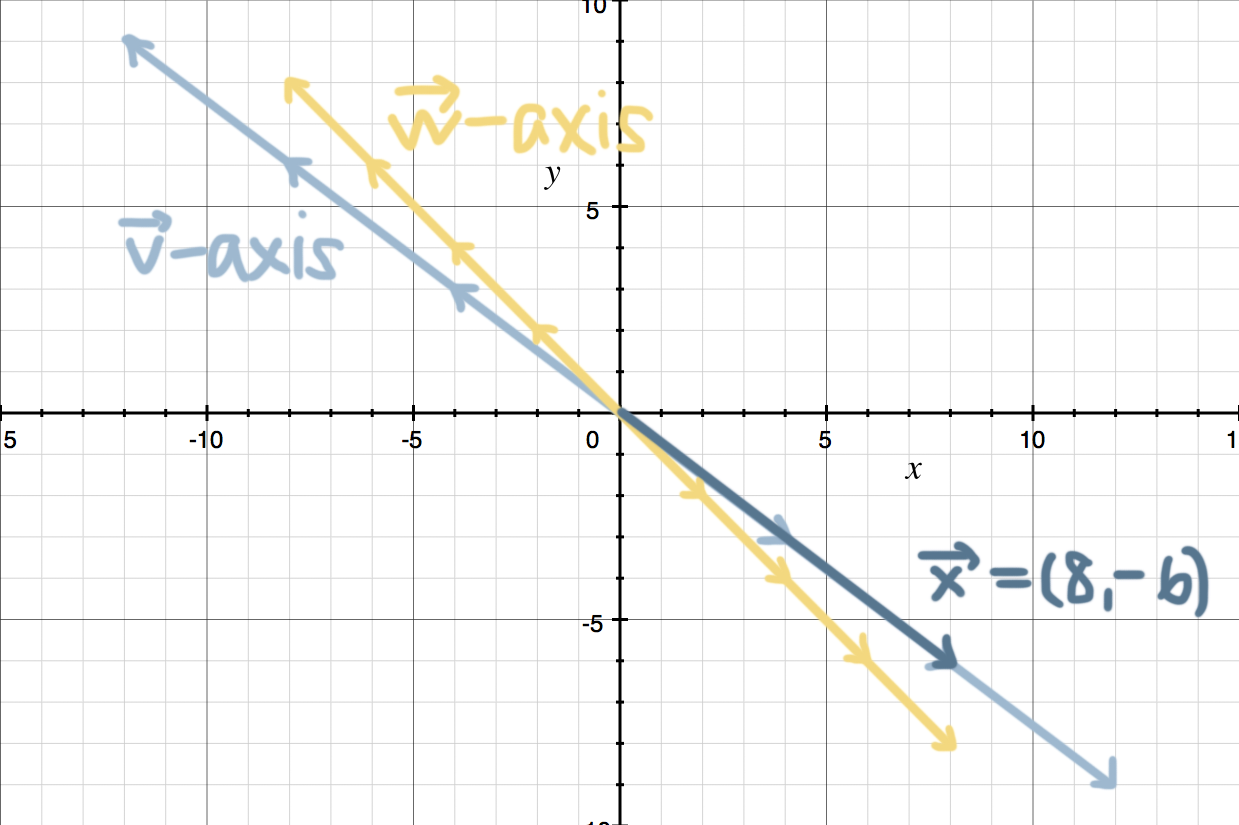
Find the combination of basis vectors $\vec{v}=(4,-3)$ and $\vec{w}=(-2,2)$, where $\vec{v}$ and $\vec{w}$ are a basis for $\mathbb{R}^2$, and give $\vec{x}=8\bold{i}-6\bold{j}$.

The vector $\vec{x}=(8,-6)$ is given in terms of the standard basis, and we need to transform it into an alternate basis that’s defined by $\vec{v}=(4,-3)$ and $\vec{w}=(-2,2)$.

In other words, we’re trying to figure out how we would represent $\vec{x}=(8,-6)$, if we were doing it in terms of $\vec{v}$ and $\vec{w}$. So let’s plug the values we’ve been given into the matrix equation.

$A[\vec{x}]_B=\vec{x}$

To find the representation of $\vec{x}$ in the alternate basis, $[\vec{x}]_B$, we’ll solve the augmented matrix.

This tells us that

$[\vec{x}]_B=\begin{bmatrix}2\\ 0\end{bmatrix}$

In other words, we need $2$ of $\vec{v}=(4,-3)$ and $0$ of $\vec{w}=(-2,2)$ in order to get to $\vec{x}=(8,-6)$, in the alternate basis space defined by $\vec{v}$ and $\vec{w}$. So if we want to sketch this result, we first sketch in our $\vec{v}$- and $\vec{w}$-axes.

Then we move out $2$ $\vec{v}$-units in the positive direction of the $\vec{v}$-axis, and $0$ $\vec{w}$-units along the $\vec{w}$-axis (which means we don’t move anywhere at all), and we arrive at $\vec{x}=(8,-6)$.

---

If we have the vectors that form the basis for the subspace, then we can use them to create a transformation matrix, called the change of basis matrix, that will change a vector from one basis to another.

When $A$ is invertible

If the basis transformation matrix is invertible (if it has an inverse), then we can multiply $A^{-1}$ by both sides of $A[\vec{x}]_B=\vec{x}$.

$A[\vec{x}]_B=\vec{x}$

$A^{-1}A[\vec{x}]_B=A^{-1}\vec{x}$

$I[\vec{x}]_B=A^{-1}\vec{x}$

$[\vec{x}]_B=A^{-1}\vec{x}$

Now we have an equation that calculates directly the expression of $\vec{x}$ in the alternate basis.

So if we were to use the values from the last example, we could have first found $A^{-1}$ from $A$.

Now that the left side of the augmented matrix is in reduced row-echelon form, the right side is the inverse matrix $A^{-1}$, so

Now to find the representation of $\vec{x}=(8,-6)$ in $B$, we simply multiply the inverse matrix by the vector.

$[\vec{x}]_B=A^{-1}\vec{x}$

$[\vec{x}]_B=\begin{bmatrix}1(8)+1(-6)\\ \frac32(8)+2(-6)\end{bmatrix}$

$[\vec{x}]_B=\begin{bmatrix}8-6\\ 12-12\end{bmatrix}$

$[\vec{x}]_B=\begin{bmatrix}2\\ 0\end{bmatrix}$

This confirms the result we found before.

---

Get access to the complete Linear Algebra course

---