Combinations of vectors (adding and subtracting vectors)
Creating the combination
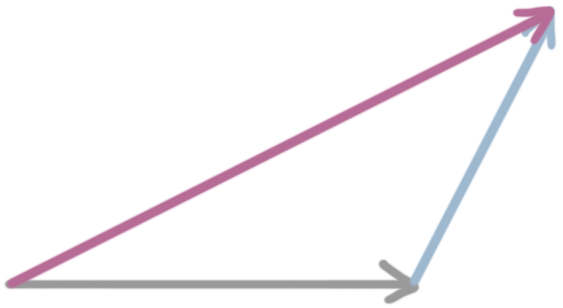
When we want to find the combination of two vectors, we take just match up the initial point of the second vector with the terminal point of the first vector, and then we draw a new third vector from the initial point of the first to the terminal point of the second. In other words, the combination of gray and blue is purple:
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Essentially, combining two vectors gives us the same result as adding the vectors. In the example above, gray + blue = purple. We can also subtract vectors. If a vector is being subtracted, we move in exactly the opposite direction of the original vector. In the example below, gray - blue = purple. The solid blue vector is the original vector, but since we’re subtracting, we move in the opposite direction.
How to calculate the combination of vectors
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Combining three vectors
Example
Find the vector combinations.
???\vec{AB}+\vec{BC}???
???\vec{BC}-\vec{AC}???
???\vec{AC}+\vec{CB}-\vec{DB}???
For ???\vec{AB}+\vec{BC}???:
The initial point of ???\vec{AB}??? is ???A???, and its terminal point is ???B???. The initial point of ???\vec{BC}??? is ???B??? (the terminal point of ???A???), and its terminal point is ???C???. Therefore, the combination of these two vectors, from the starting point of the first to the ending point of the last, is
???\vec{AB}+\vec{BC}=\vec{AC}???
If a vector is being subtracted, we move in exactly the opposite direction of the original vector.
For ???\vec{BC}-\vec{AC}???:
When two vectors are subtracted, we can change the negative vector to positive by flipping the direction of the vector. In this case, ???-\vec{AC}??? becomes ???+\vec{CA}???. Then we just combine them as normal.
???\vec{BC}-\vec{AC}=\vec{BC}+\vec{CA}???
???\vec{BC}-\vec{AC}=\vec{BA}???
For ???\vec{AC}+\vec{CB}-\vec{DB}???:
We’ll start by changing the negative vector to a positive by flipping the direction of the vector. In this case, ???-\vec{DB}??? becomes ???+\vec{BD}???. We’ll get rid of the negative and then combine the vectors two at a time.
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AC}+\vec{CB}+\vec{BD}???
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AB}+\vec{BD}???
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AD}???