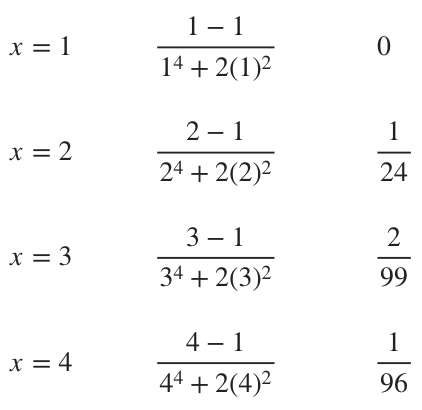Comparison theorem for improper integrals
Formulas for the comparison theorem
The comparison theorem for improper integrals is very similar to the comparison test for convergence that you’ll study as part of Sequences & Series.
It allows you to draw a conclusion about the convergence or divergence of an improper integral, without actually evaluating the integral itself.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
It states:
If ???f(x)\geq g(x)\geq 0??? on ???[a,\infty)???, then
If ???\int_a^\infty f(x)\ dx??? converges then so does ???\int_a^\infty g(x)\ dx???
If ???\int_a^\infty g(x)\ dx??? diverges then so does ???\int_a^\infty f(x)\ dx???
Notice that it does not state:
If ???f(x)\geq g(x)\geq 0??? on ???[a,\infty)???, then
If ???\int_a^\infty g(x)\ dx??? converges then so does ???\int_a^\infty f(x)\ dx???
If ???\int_a^\infty f(x)\ dx??? diverges then so does ???\int_a^\infty g(x)\ dx???
The comparison theorem will allow you to draw the first two conclusions, but not the others. The reason is that we’re assuming ???f(x)\geq g(x)???.
Thinking about ???f(x)???:
If ???f(x)??? is greater than (above) ???g(x)???, then if ???f(x)??? converges, we know it will force ???g(x)??? to also converge. But if ???f(x)??? diverges, then we can’t draw any conclusion about ???g(x)??? because ???g(x)??? could diverge or converge below it.
Thinking about ???g(x)???:
If ???g(x)??? is less than (below) ???f(x)???, then if ???g(x)??? diverges, we know it will force ???f(x)??? to also diverge. But if ???g(x)??? converges, then we can’t draw any conclusion about ???f(x)??? because ???f(x)??? could diverge or converge above it.
Given an improper integral and asked to use comparison theorem to say whether it converges or diverges, our goal will be to find a comparison function that we know will either always be greater than the given function, or always be less than the given function.
Since ???f(x)\geq g(x)??? in the comparison theorem:
If we find a comparison function that is always greater than the given function, then the given function will be ???g(x)??? and the comparison function will be ???f(x)???.
In this case, in order to use the comparison theorem to draw a conclusion, we’d have to show that the comparison function ???f(x)??? converges. If we can show that the comparison function ???f(x)??? converges, then we’ve proven that the given function ???g(x)??? also converges.
If we find a comparison function that is always less than the given function, then the given function will be ???f(x)??? and the comparison function will be ???g(x)???.
In this case, in order to use the comparison theorem to draw a conclusion, we’d have to show that the comparison function ???g(x)??? diverges. If we can show that the comparison function ???g(x)??? diverges, then we’ve proven that the given function ???f(x)??? also diverges.
Using the comparison theorem to determine the convergence of an improper integral
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Say whether the integral converges or diverges by applying the comparison theorem
Example
Use the comparison theorem to say whether the integral converges or diverges.
???\int_1^\infty\frac{x-1}{x^4+2x^2}\ dx???
Often it’s really helpful to try to make a guess about whether the given function is converging or diverging so that we know whether to look for a comparison function that is greater than or less than the given function.
If we guess that the given function is converging, we’ll look for a comparison function that is greater than the given function, so that we can show that the comparison function is converging, and therefore prove that the given function is converging.
If we guess that the given function is diverging, we’ll look for a comparison function that is less than the given function, so that we can show that the comparison function is diverging, and therefore prove that the given function is diverging.
Since the interval is ???[1,\infty)???, let’s plug in the first few values, ???x=1???, ???x=2???, ???x=3???, etc.
our goal will be to find a comparison function that we know will either always be greater than the given function, or always be less than the given function.
These values seem to be approaching ???0???, so we’ll guess that the given function is converging. Which means we want to look for a comparison function that is greater than the given function, and hope that the comparison function will converge, proving that the given function also converges.
The only way to make a fraction bigger is to make the numerator bigger and/or to make the denominator smaller. If we just take away the ???-1??? from the numerator of the given function, that would immediately make the numerator larger, because we wouldn’t be subtracting ???1??? from it. So we know right away that the comparison function
???\int_1^\infty\frac{x}{x^4+2x^2}\ dx???
will be larger than the given function. We can factor out an ???x??? and simplify this comparison function to
???\int_1^\infty\frac{1}{x^3+2x}\ dx???
We know this comparison function will get even larger if we can make the denominator smaller. Taking away the ???2x??? would make the denominator smaller, so our comparison function will simplify to
???\int_1^\infty\frac{1}{x^3}\ dx???
We know that
???\frac{1}{x^3}>\frac{x-1}{x^4+2x^2}???
and that the comparison function is therefore ???f(x)???, that the given function is ???g(x)???, and that we’re looking to show that the comparison function ???f(x)??? converges, which will prove that the given function ???g(x)??? also converges.
For functions in the form
???\frac{1}{x^p}???
If ???p>1??? then the function converges
If ???p<1??? then the function diverges
Therefore, since ???3>1??? we can say that the comparison function converges, which proves that the given function also converges.