Triangle congruence with SSS, ASA, SAS
How to use triangle congruence theorems to prove that two triangles are congruent
In this lesson we’ll look at how to use triangle congruence theorems to prove that triangles, or parts of triangles, are congruent to one another.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Congruent triangles
A pair of congruent triangles have exactly the same size and shape. That means that all pairs of sides are the same length and all pairs of angles have the same measure.
You know that triangles are congruent to one another if the pairs of sides and angles are congruent. The good news is you don’t have to show that all six pairs match up. There are some triangle theorems that you can use as a short cut to prove two triangles are congruent.
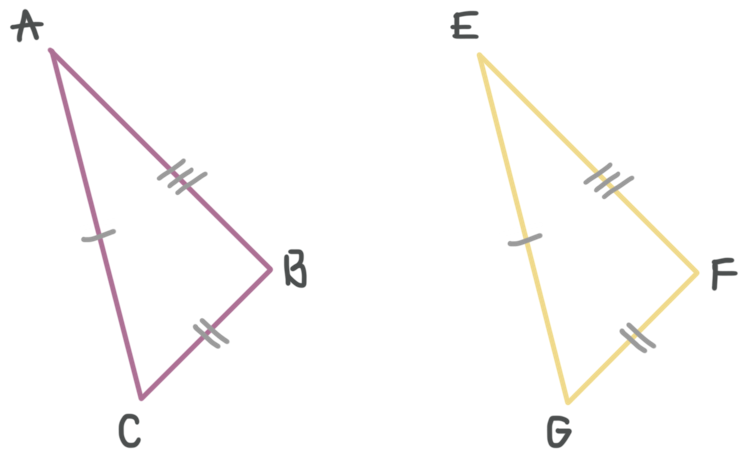
Side, side, side (SSS)
If you can show that all three side pairs are congruent, then you’ll have proven that the triangles are congruent, without needing to check any of the angles. In the figure below, ???\triangle ABC\cong \triangle EFG??? by side, side, side.
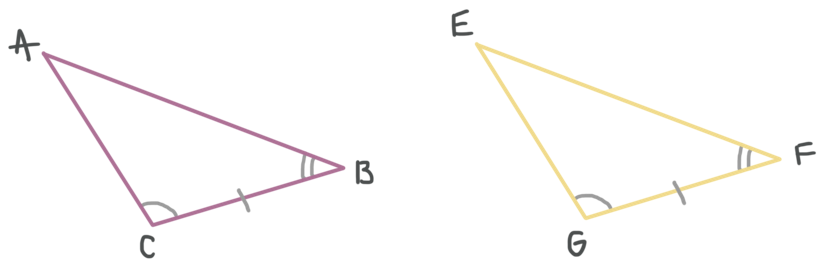
Angle, side, angle (ASA)
For “angle, side, angle” you need to have two angles and the side in between them (the side that’s touching both angles) to be congruent. If you can find this pattern in the triangle, then you’ve proven that the triangles are congruent, without checking the third angle or the other two sides. In the figure below, ???\triangle ABC\cong \triangle EFG??? by angle, side, angle.
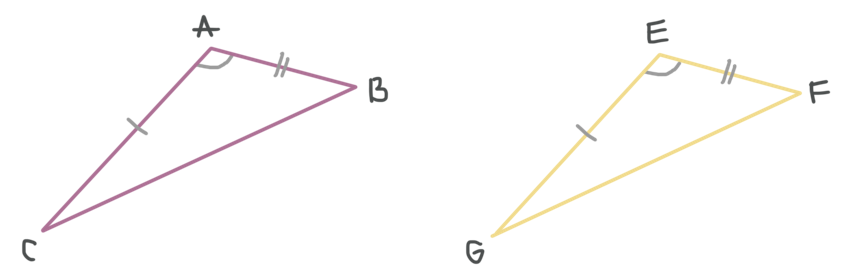
Side, angle, side (SAS)
For triangles to be congruent by “side, angle, side” you need to have two congruent sides that together form the vertex of the same angle. If you can show that two sides are congruent, and that their included angle is also congruent, then you’ve proven that the triangles are congruent, without needing to check the third side or the other two angles. In the figure below, ???\triangle ABC\cong \triangle EFG??? by side, angle, side.
Matching congruent parts
Whenever you state that two triangles are congruent, you must match the letters for corresponding vertices when you name the triangles.
Even if the letters for the vertices of one of the triangles are in alphabetical order, the letters for the corresponding vertices of the other triangle will not necessarily be in alphabetical order. Write the names so that the letters for the vertices are in the same places. Then the letters for the endpoints of pairs of congruent sides will also be in the same places.
If we have a pair of congruent triangles, ???\triangle ABC??? and ???\triangle DEF???, then the triangle congruency statement ???\triangle ABC\cong\triangle DEF??? means that all of the following are true:
The letters ???A???, ???B???, and ???C??? for the vertices of ???\triangle ABC??? correspond to the letters ???D???, ???E???, and ???F???, respectively, for the vertices of ???\triangle DEF???.
Side ???\overline{AB}??? in ???\triangle ABC??? is congruent to side ???\overline{DE}??? in ???\triangle DEF???.
Side ???\overline{BC}??? in ???\triangle ABC??? is congruent to side ???\overline{EF}??? in ???\triangle DEF???.
Side ???\overline{AC}??? in ???\triangle ABC??? is congruent to side ???\overline{DF}??? in ???\triangle DEF???.
For instance, in the figure above, it would be correct to say that ???\triangle ABC\cong \triangle EFG??? because angles ???A??? and ???E??? are congruent, angles ???B??? and ???F??? are congruent, and angles ???C??? and ???G??? are congruent. But it would be incorrect to say ???\triangle ABC\cong \triangle GFE???, since this statement doesn’t list the letters for the vertices of the triangle on the right (in the figure) in the same order as the letters for the corresponding vertices of the triangle on the left. In other words, we can actually state the congruence of the triangles in any of these ways:
???\triangle ABC\cong \triangle EFG???
???\triangle BCA\cong \triangle FGE???
???\triangle CAB\cong \triangle GEF???
???\triangle ACB\cong \triangle EGF???
???\triangle BAC\cong \triangle FEG???
???\triangle CBA\cong \triangle GFE???
Triangle congruence rules for SSS, ASA, and SAS
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Three examples of writing the triangle congruency statement
Example
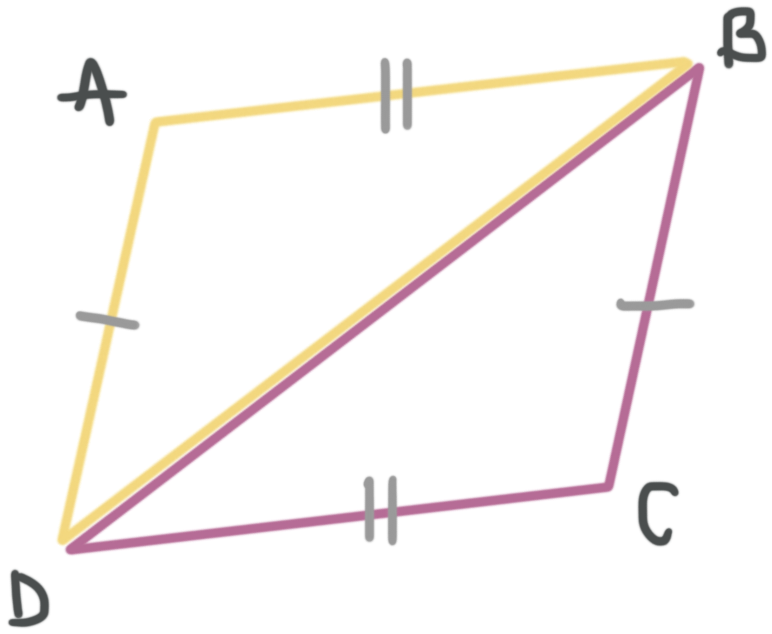
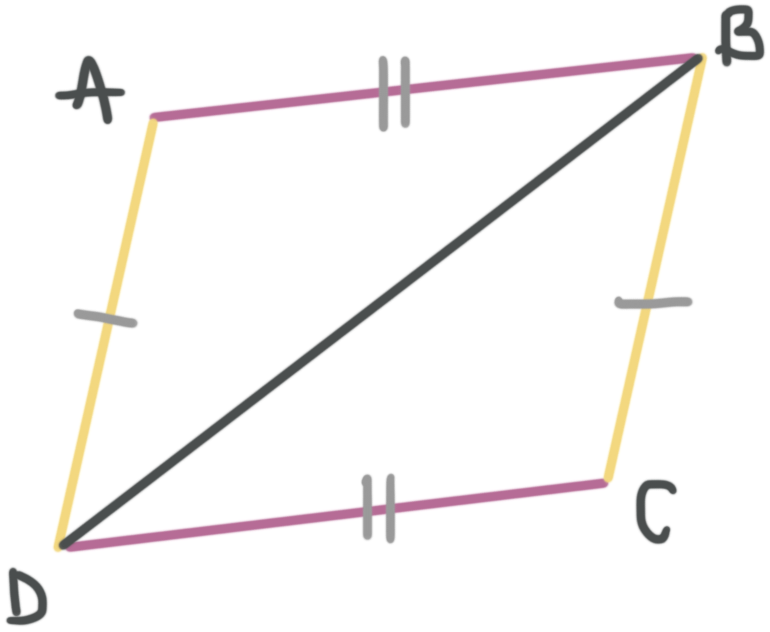
Name the pair of congruent triangles in a congruence statement and state how the triangles are congruent.
When we look at the two triangles we know that ???\overline{AB}\cong \overline{CD}??? and that ???\overline{AD}\cong \overline{CB}???. We also know that side ???\overline{DB}??? is congruent to itself, so ???\overline{DB}\cong \overline{DB}???. This means we have three congruent side pairs, so we can prove triangle congruence by side, side, side.
We need to name the triangles by matching the corresponding sides. Sometimes color coding the triangles can help you match up the names.
We can then write the congruence statement as
???\triangle ABD\cong \triangle CDB???
Let’s try two more.
For triangles to be congruent by “side, angle, side” you need to have two congruent sides that together form the vertex of the same angle.
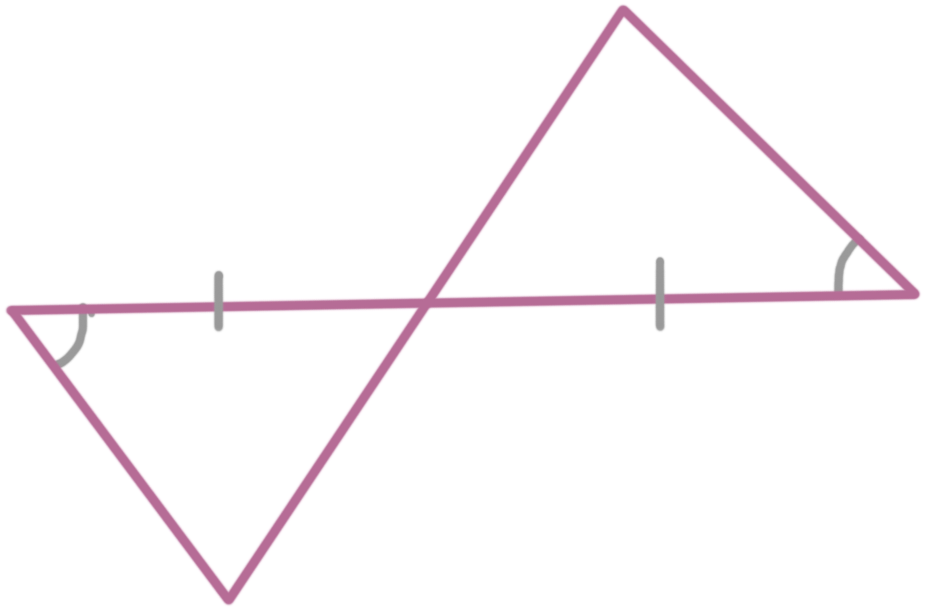
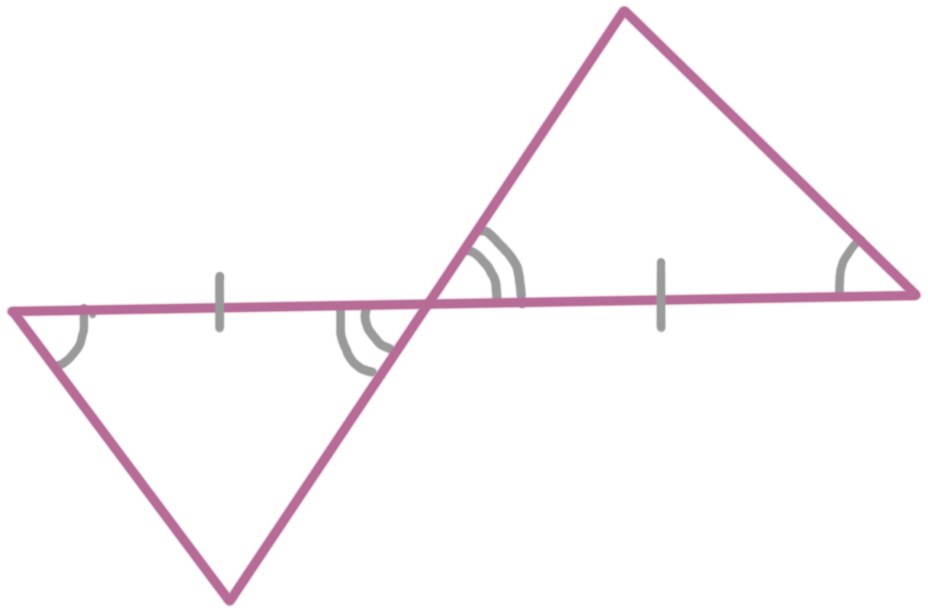
Example
State how the triangles are congruent.
In these two triangles, we have a congruent angle pair and a congruent side pair. You also have a pair of vertical angles here:
Remember that vertical angles are congruent to one another, so we can say that these two triangles are congruent by ASA.
Let’s do the last example.
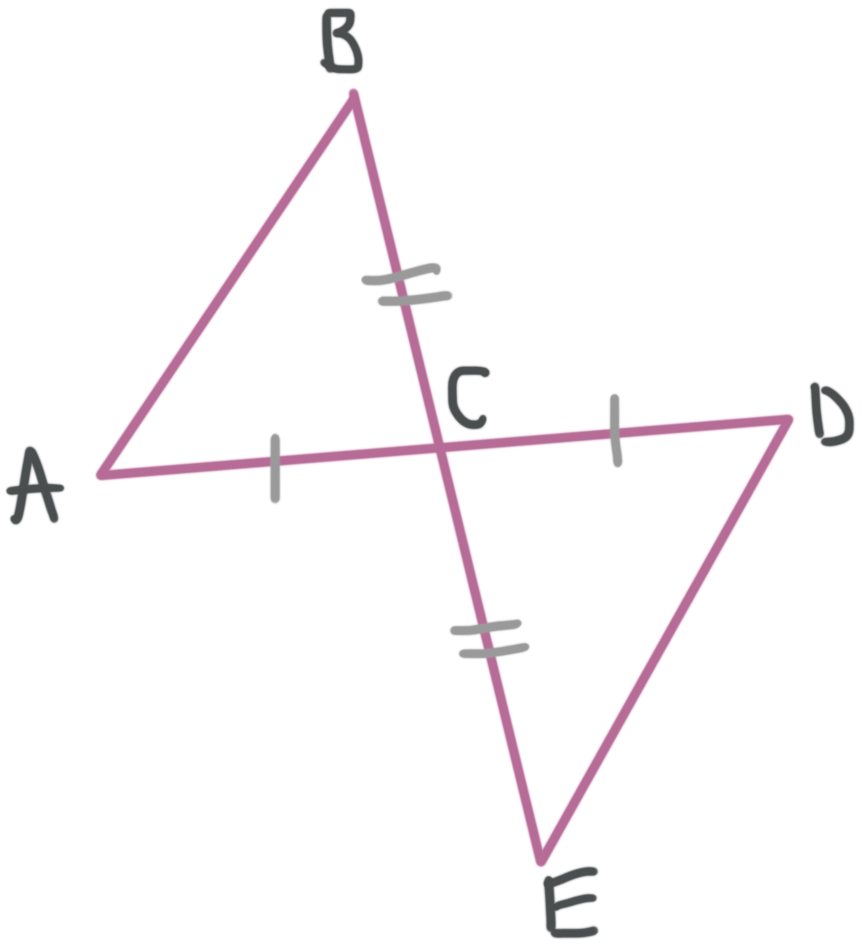
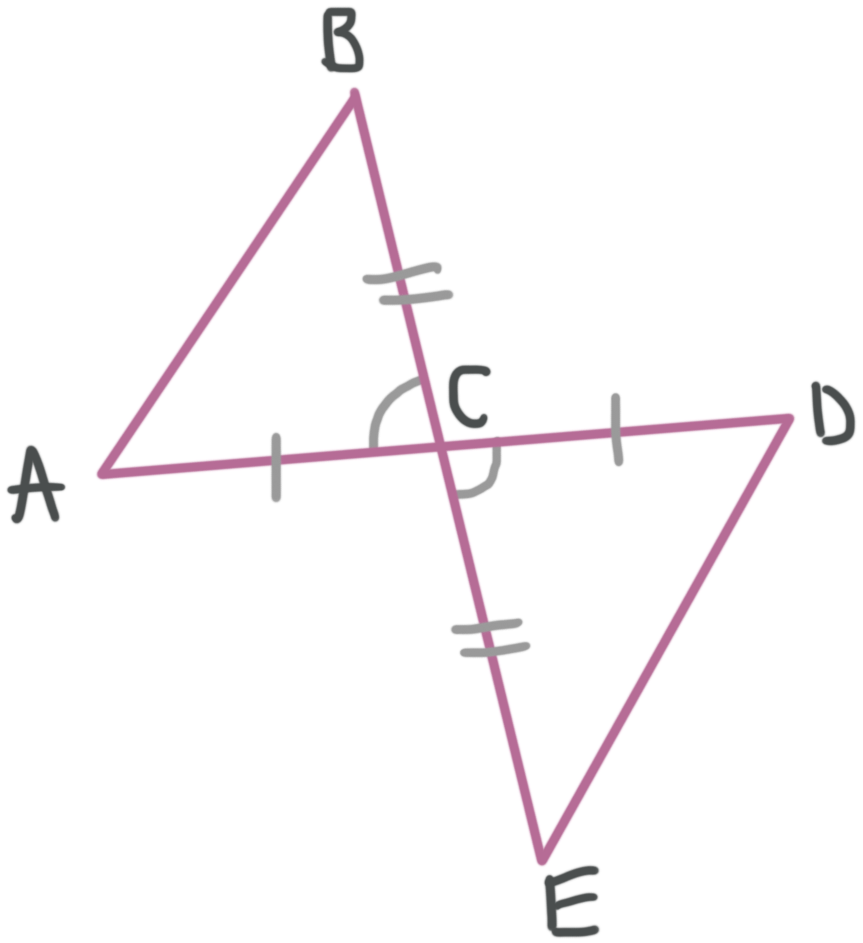
Example
State how the triangles are congruent and write the triangle congruency statement for the pair of them.
The diagram tells us that ???\overline{AC}\cong \overline{DC}??? and ???\overline{BC}\cong \overline{EC}???. We also know that ???\angle BCA\cong \angle ECD??? because they are vertical angles.
This means ???\triangle ABC\cong \triangle DEC??? by SAS.