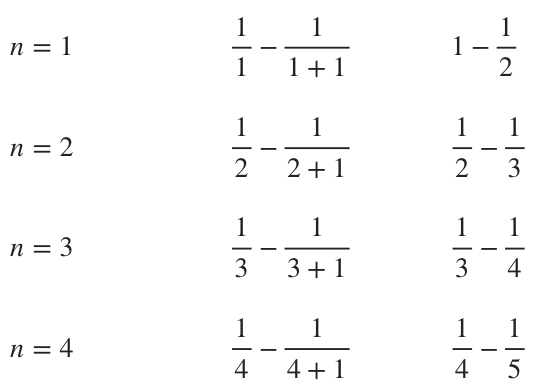Convergence of a telescoping series

Defining the convergence of a telescoping series

Telescoping series are series in which all but the first and last terms cancel out. If you think about the way that a long telescope collapses on itself, you can better understand how the middle of a telescoping series cancels itself.

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

To determine whether a series is telescoping, we’ll need to calculate at least the first few terms to see whether the middle terms start canceling with each other.

Convergence of the telescoping series

To see whether or not a telescoping series converges or diverges, we’ll need to look at its series of partial sums $s_n$ , which is just the sum of the series through the first $n$ terms.

$s_n=\sum_{i=1}^n a_i=a_1+a_2+...+a_n$

Looking at this equation for $s_n$ , we can imagine that the sum of the series through the first four terms would be the partial sum $s_4$ , or

$s_4=\sum_{i=1}^4 a_i=a_1+a_2+a_3+a_4$

$s_4=a_1+a_2+a_3+a_4$

What we want to figure out is whether or not we’ll get a real-number answer when we take the sum of the entire series, because if we take the sum of the entire series and we get a real-number answer, this means that the series converges. Otherwise, if the sum of the entire series turns out to be infinite, that means the series diverges. In other words, we want to get a real-number answer $s$ , when we use an infinite number of terms $n$ in the series of partial sums $s_n$ . $s$ is the sum of the series, where

$s=\lim_{n\to\infty}s_n=\sum_{n=1}^\infty a_n=a_1+a_2+a_3+...+a_n$

So if we calculate the limit as $n\to\infty$ of $s_n$ and we get a real-number answer $s$ , then we can say that the series of partial sums $s_n$ converges, and this lets us also conclude that the series $a_n$ converges. If we cannot find a real-number answer for $s$ , then $s_n$ diverges, and therefore $a_n$ also diverges.

To find $s_n$ , we’ll expand the telescoping series by calculating the first few terms, making sure to also include the last term of the series, then simplify the sum by canceling all of the terms in the middle. The remaining series will be the series of partial sums $s_n$ .

How to determine the convergence or divergence of a telescoping series

Take the course

Want to learn more about Calculus 2? I have a step-by-step course for that. :)

Learn More

Say whether the telescoping series converges or diverges

Example

Show that the series is a telescoping series, then say whether the series converges or diverges.

$\sum^{\infty}_{n=1}\frac{1}{n}-\frac{1}{n+1}$

In order to show that the series is telescoping, we’ll need to start by expanding the series. Let’s use $n=1$ , $n=2$ , $n=3$ and $n=4$ .

Writing these terms into our expanded series and including the last term of the series, we get

$s=\lim_{n\to\infty}s_n=\sum^{\infty}_{n=1}\frac{1}{n}-\frac{1}{n+1}$

$=\lim_{n\to\infty}\left[\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right)+...+\left(\frac{1}{n}-\frac{1}{n+1}\right)\right]$

The series is telescoping if we can cancel all of the terms in the middle (every term but the first and last). When we look at our expanded series, we see that the second half of the first term will cancel with the first half of the second term, that the second half of the second term will cancel with the first half of the third term, and so on, so we can say that the series is telescoping.

Convergence of a telescoping series for Calculus 2.jpg — The series is telescoping if we can cancel all of the terms in the middle (every term but the first and last).

Canceling everything but the first half of the first term and the second half of the last term gives an expression for the series of partial sums.

$s=\lim_{n\to\infty}s_n=\lim_{n\to\infty}1-\frac{1}{n+1}$

If this series of partial sums $s_n$ converges as $n\to\infty$ (if we get a real-number value for $s$ ), then we can say that the series of partial sums converges, which allows us to conclude that the telescoping series $a_n$ also converges.

$s=\lim_{n\to\infty}1-\frac{1}{n+1}$

$s=\lim_{n\to\infty}1-\frac{\frac{1}{n}}{\frac{n}{n}+\frac{1}{n}}$

$s=\lim_{n\to\infty}1-\frac{\frac{1}{n}}{1+\frac{1}{n}}$

$s=1-\frac{0}{1+0}$

$s=1-0$

$s=1$

Since $s$ exists as a real number, the sum of the series is $s=1$ , and we can conclude that the series of partial sums $s_n$ converges, and therefore that the series $a_n$ also converges.