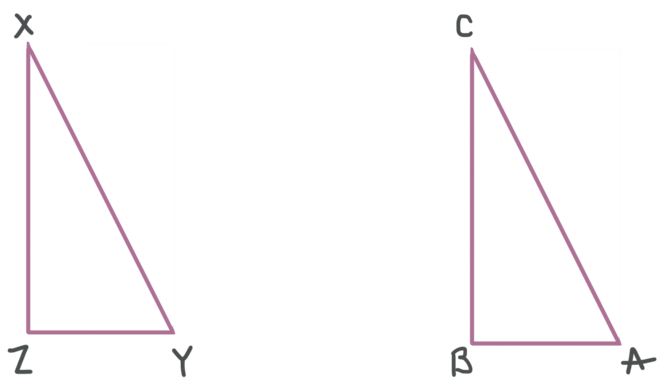Congruent parts of congruent triangles are congruent (CPCTC)

What is the CPCTC theorem? (Congruent parts of congruent triangles are congruent.)

CPCTC stands for “corresponding parts of congruent triangles are congruent.”

In some of the previous lessons on congruence, we used congruent parts of a pair of triangles to try to prove that the triangles themselves are congruent.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

CPCTC flips this around, and makes the point that, given two congruent triangles, corresponding parts of those triangles must also be congruent.

In other words, we can place one of the triangles on top of the other in such a way that all three pairs of corresponding sides are congruent and all three pairs of corresponding angles are congruent. Remember that when you state that two triangles are congruent, you need to name them with the letters for corresponding vertices in the same order.

For example, if you know the two triangles below are congruent, you need to match up the letters for their corresponding vertices, and then use those to state the congruences of angles and sides.

In the figure above, we see that the letters $A$, $B$, and $C$ for the vertices of $\triangle ABC$ correspond to the letters $Y$, $Z$, and $X$, respectively, for the vertices of $\triangle XYZ$, so these triangles match in this way:

Now that the letters for the vertices are matched up, you can state the congruences of angles and sides.

Angle congruences: $\angle A\cong \angle Y$, $\angle B\cong \angle Z$, and $\angle C\cong \angle X$

Side congruences: $\overline{AB}\cong\overline{YZ}$, $\overline{BC}\cong\overline{ZX}$, and $\overline{AC}\cong\overline{YX}$

Now we name the congruent triangles so that the letters for corresponding vertices match up in the triangle congruency statement.

$\triangle ABC\cong \triangle YZX$

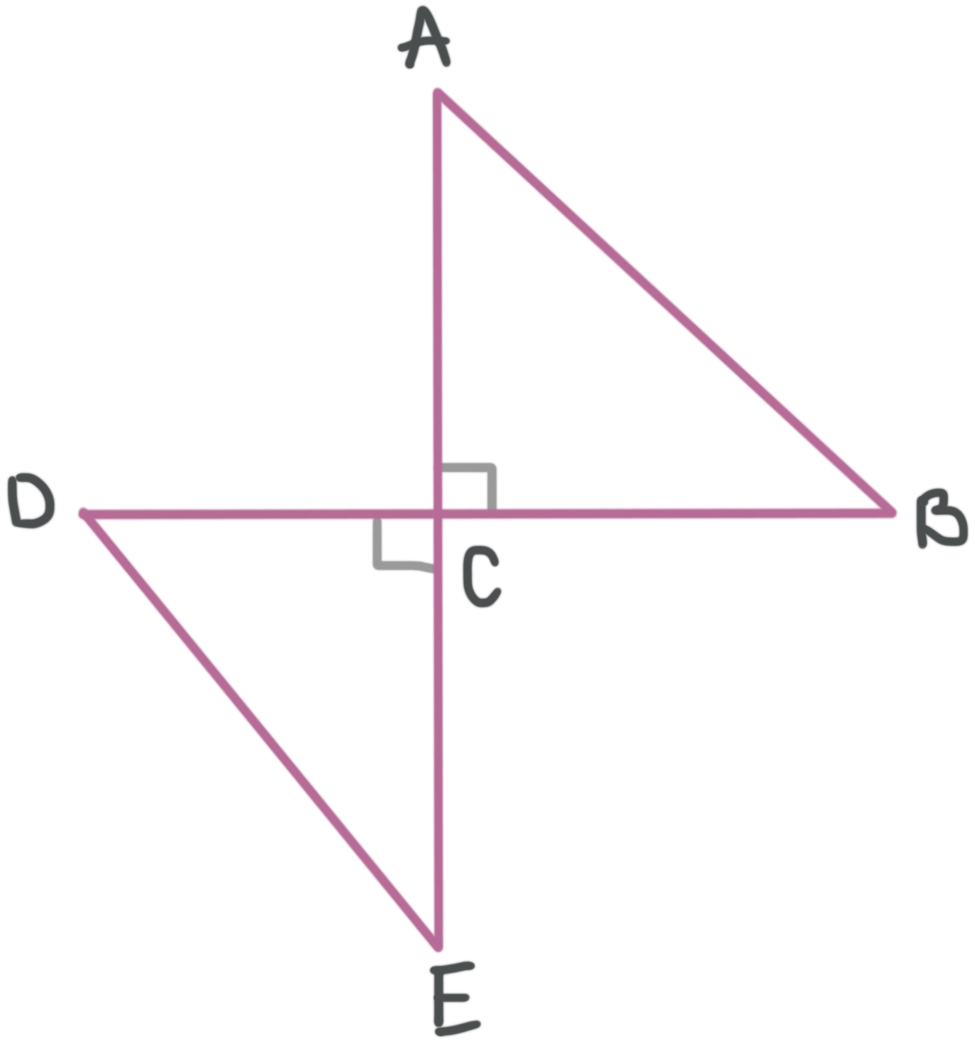
This would also work if you were given the triangle congruency statement. For instance, say we’re given that $\triangle CED\cong \triangle CAB$.

Then from this statement alone (even if we didn’t have the figure) we could match up the letters for the corresponding vertices, and then use those to state congruences of sides.

$\triangle CED\cong \triangle CAB$

This statement tells us that the letters $C$, $E$, and $D$ for the vertices of $\triangle CDE$ correspond to the letters $C$, $A$, and $B$, respectively, for the vertices of $\triangle CAB$. Therefore,

$\overline{CE}\cong \overline{CA}$

$\overline{ED}\cong \overline{AB}$

$\overline{CD}\cong \overline{CB}$

Finally, you can use the figure to state congruences of angles.

$\angle DCE\cong\angle BCA$

$\angle CED\cong\angle CAB$

$\angle CDE\cong\angle ABC$

How to use CPCTC to determine that triangles are congruent

---

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

---

Writing congruency statements about triangles using CPCTC

Example

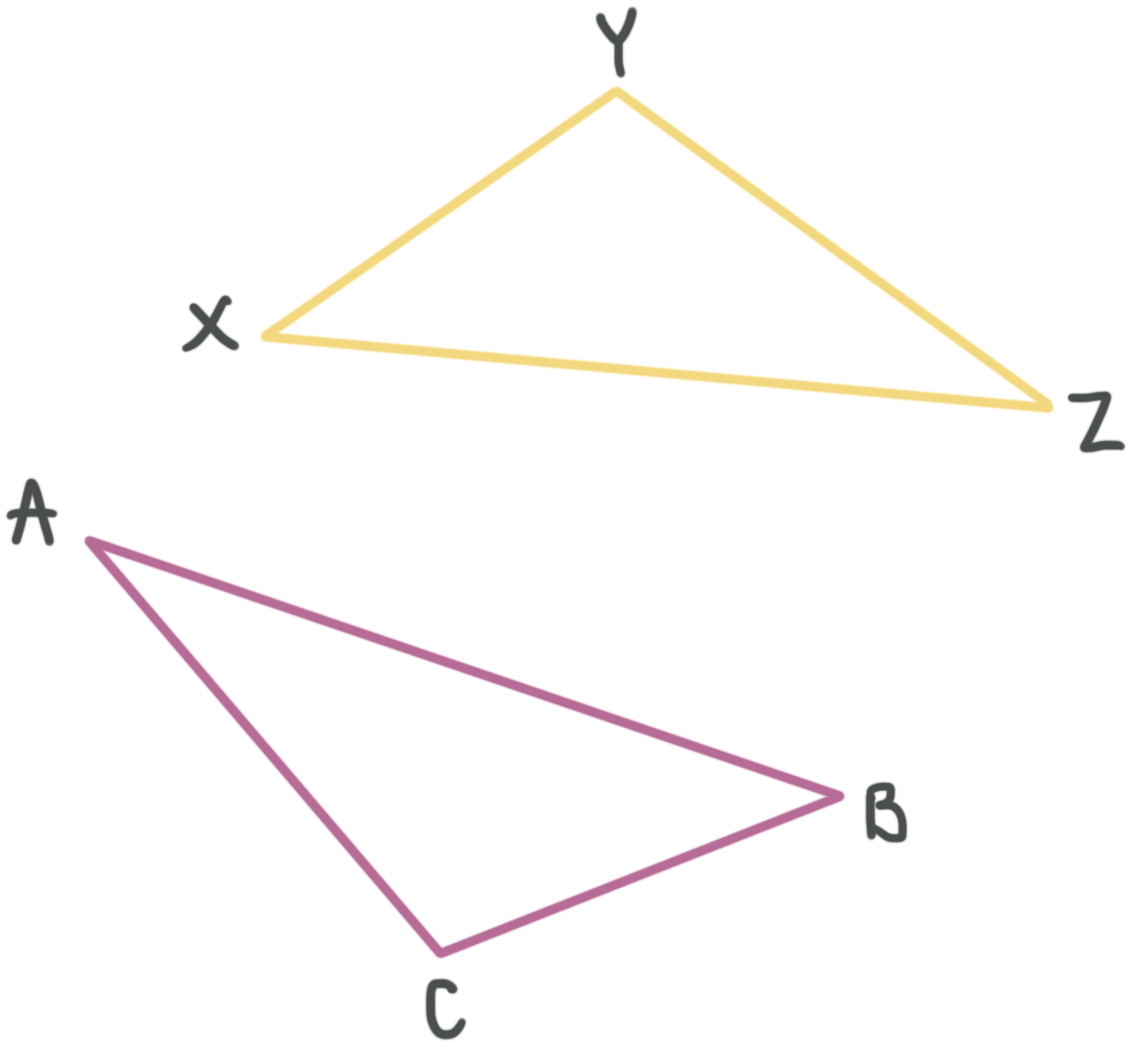
Complete the congruency statement by naming the corresponding angle to $\angle XZY$, given that $\triangle ABC\cong \triangle ZXY$.

We know that $\triangle ABC\cong \triangle ZXY$, so the corresponding angle pairs are

$\angle A\cong \angle Z$

$\angle B\cong \angle X$

$\angle C\cong \angle Y$

The triangles match like this:

Now we can find the corresponding angle to $\angle XZY$.

The congruency statement between those angles is then $\angle XZY\cong \angle BAC$.

---

Let’s try another example.

---

CPCTC flips this around, and makes the point that, given two congruent triangles, corresponding parts of those triangles must also be congruent.

Example

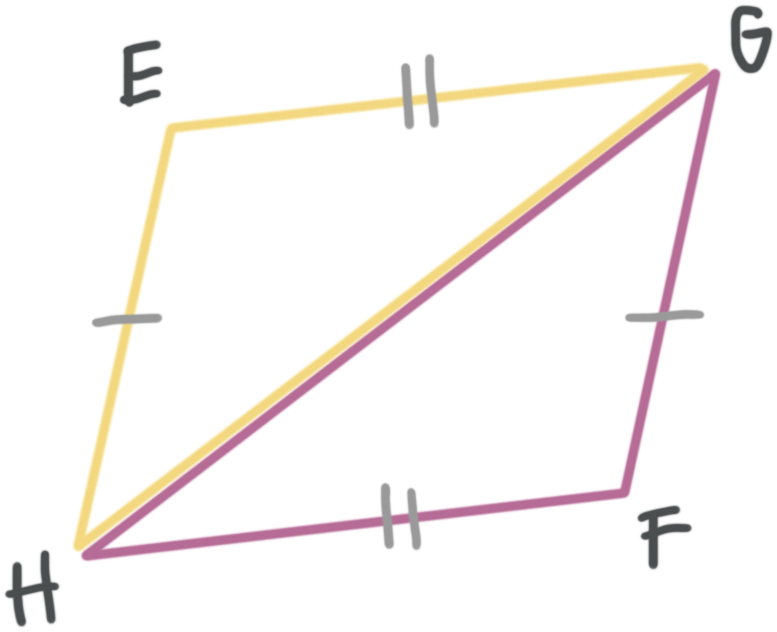
These two triangles are congruent by side, side, side. Write the congruency statement for the triangles.

Match up the corresponding parts.

The congruent angle pairs are

$\angle E\cong \angle F$

$\angle G\cong \angle H$

$\angle H\cong \angle G$

From the matched up angle, we can write any of these congruency statements:

$\triangle EGH\cong \triangle FHG$

$\triangle GHE\cong \triangle HGF$

$\triangle HEG\cong \triangle GFH$

As you can see, there’s more than one correct way to write the statement. As long as the corresponding parts match up, the congruency statement is correct.

---

Get access to the complete Geometry course

---