How to determine whether a function is even, odd, or neither
What are even and odd functions?
When we talk about “even, odd, or neither” we’re talking about the symmetry of a function. It’s easiest to visually see even, odd, or neither when looking at a graph. Sometimes it’s difficult or impossible to graph a function, so there is an algebraic way to check as well.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Even functions
Symmetric about the ???y???-axis
When you plug ???-x??? into the function, it will simplify to be the same as the original function. This means that it doesn’t matter whether you plug in ???x??? or ???-x???, your output will be the same. So
???f(-x)=f(x)???
Below are graphs that are even and symmetric about the ???y???-axis.
Odd functions
Symmetric about the origin
When you plug ???-x??? into the function, it will simplify to be negative of the original function, or the original function multiplied by ???-1???. This means that when you plug ???-x??? into the function, you’ll get the same output as you do when you plug in ???x???, except it will be negative (or have the opposite sign as the original output). So
???f(-x)=-f(x)???
Below are graphs that are odd and symmetric about the origin. Be sure to visually compare quadrants that are diagonal from each other (quadrants 1 and 3, and quadrants 2 and 4).
Neither even nor odd
Not symmetric about the ???y???-axis, and not symmetric about the origin
The function has no symmetry. It’s possible that a graph could be symmetric to the ???x???-axis, but then it wouldn’t pass the Vertical Line Test and therefore wouldn’t be a function.
How to determine whether a function is even, odd, or neither
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
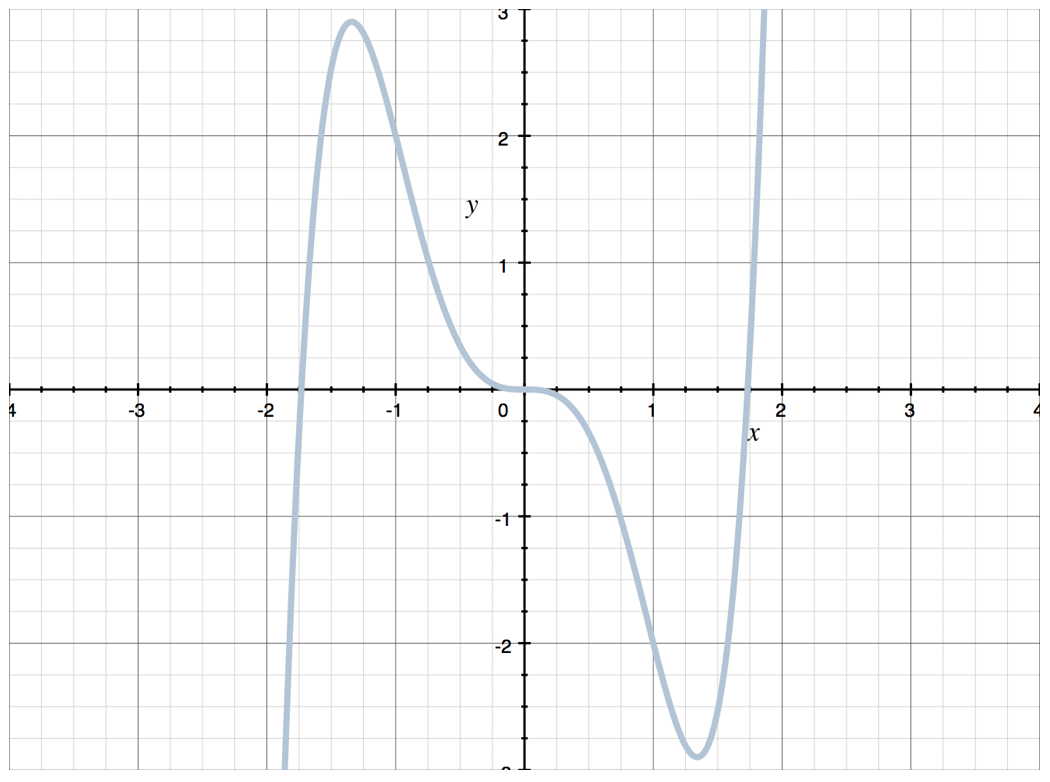
Is the polynomial function even, odd, or neither?
Example
Is the function even, odd, or neither?
???f(x)=x^5-3x^3???
To solve algebraically we need to find ???f(-x)???, so we’ll replace all ???x???’s with ???-x???.
???f(-x)=(-x)^5-3(-x)^3???
Raising a negative value to an odd exponent keeps the sign the same.
???f(-x)=-x^5+3x^3???
Factor out a negative.
???f(-x)=-\left(x^5-3x^3\right)???
Since ???f(-x)=-f(x)???, the function is odd. We can see that the graph is symmetric to the origin.
Let’s try another example of even, odd, neither.
It’s easiest to visually see even, odd, or neither when looking at a graph.
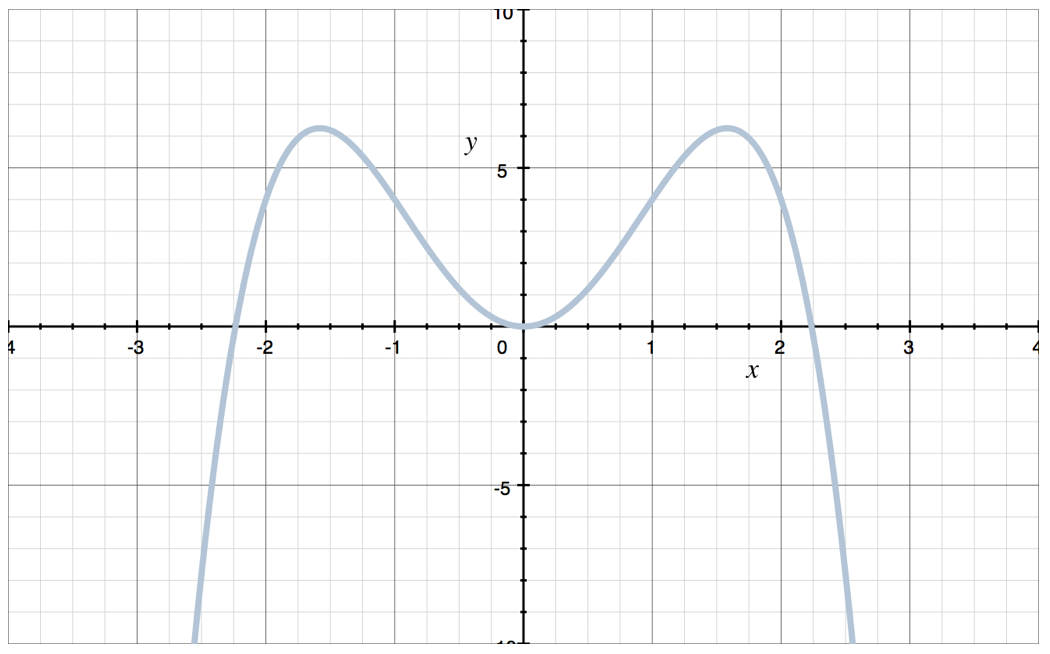
Example
Is the function even, odd, or neither?
???f(x)=5x^2-x^4???
To solve algebraically, we need to find ???f(-x)???, so we’ll replace all ???x???’s with ???-x???.
???f(-x)=5(-x)^2-(-x)^4???
Raising a negative value to an even exponent changes the sign.
???f(-x)=5x^2-x^4???
Since ???f(-x)=f(x)???, the function is even. We can see that the graph is symmetric to the ???y???-axis.