Exterior angles of polygons
Exterior vs. interior angles
In this lesson we’ll look at exterior angles of polygons and the relationship between those and their corresponding interior angles.
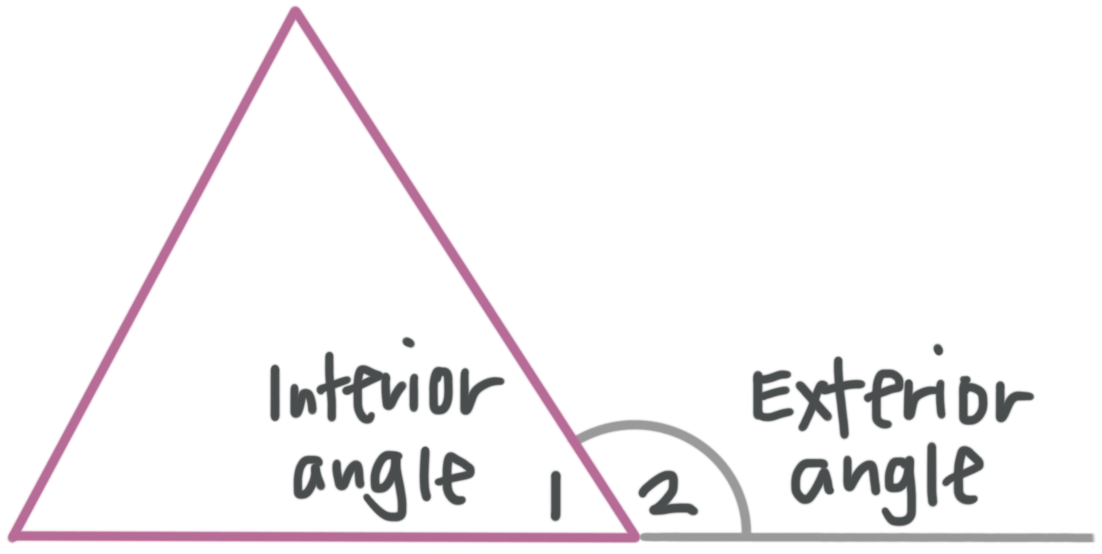
An exterior angle of a polygon is an angle that’s supplementary to one of the interior angles of the polygon, has its vertex at the vertex of that interior angle, and is formed by extending one of the two sides of the polygon (at that vertex) in the direction opposite (???180^\circ??? away from) that side.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Realize that at each vertex of a polygon there are two exterior angles: one formed by extending one of the two sides at that vertex, and one formed by extending the other side at that vertex. Since both of the exterior angles at a given vertex are supplementary to the same interior angle, the two exterior angles always have equal measure.
This means that, in the figure above, ???m\angle 1+m\angle 2=180{}^\circ???.
The sum of the measures of the exterior angles in any polygon is ???360^\circ??? if we include only one of the two exterior angles at each vertex, which is what we’ll mean going forward when we talk about a polygon’s exterior angles. Here is an example of the exterior angles of a pentagon adding to ???360^\circ???.
Remember also that the sum of the measures of the interior angles of a polygon with ???n??? sides is ???(n-2)180{}^\circ???.
How to solve for the measures of exterior angles
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Using interior angles to find the measures of the exterior angles of the polygon
Example
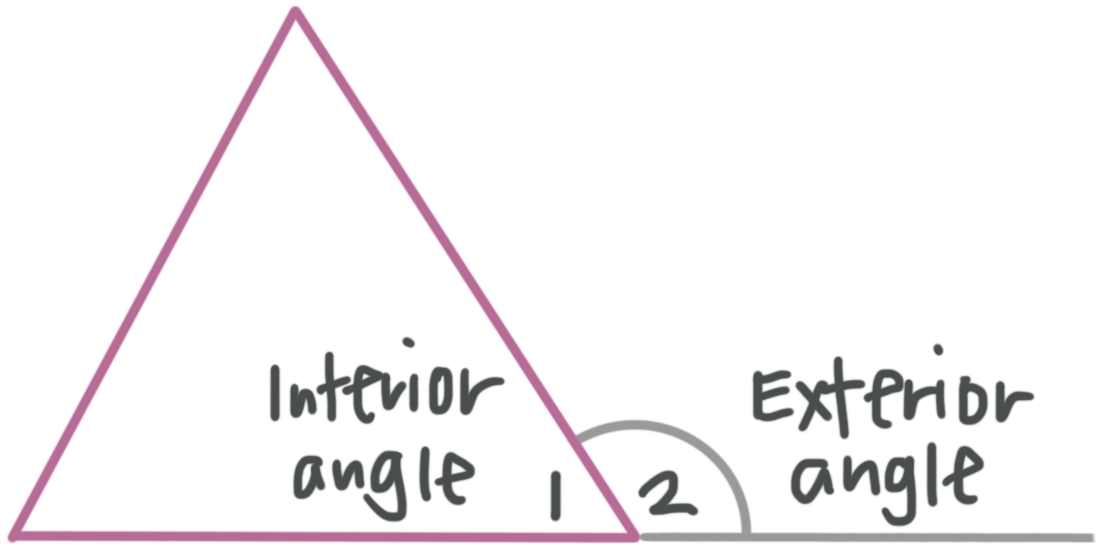
Given that the triangle in the diagram is equilateral, what is the measure of angle ???2???? (“Lateral” means “side,” so an equilateral polygon is a polygon in which all sides have equal length.)
The interior angles in a triangle add to ???180{}^\circ???. An equilateral triangle is also equiangular. That means each angle measures ???180{}^\circ \div 3=60{}^\circ???, so ???m\angle 1=60{}^\circ???. ???\angle 1??? and ???\angle 2??? are supplementary, which means
???m\angle 1+m\angle 2=180{}^\circ???
???60{}^\circ +m\angle 2=180{}^\circ???
???m\angle 2=120{}^\circ???
We could also have solved this problem by using the fact that all of the exterior angles sum to ???360{}^\circ???. A triangle has three interior angles, so it also has three exterior angles. Since all of the interior angles are congruent, all of the exterior angles will also be congruent. This means ???m\angle 2=360{}^\circ \div 3=120{}^\circ???.
Let’s look at a few more example problems.
An exterior angle of a polygon is an angle that’s supplementary to one of the interior angles of the polygon, has its vertex at the vertex of that interior angle, and is formed by extending one of the two sides of the polygon in the direction opposite that side.
Example
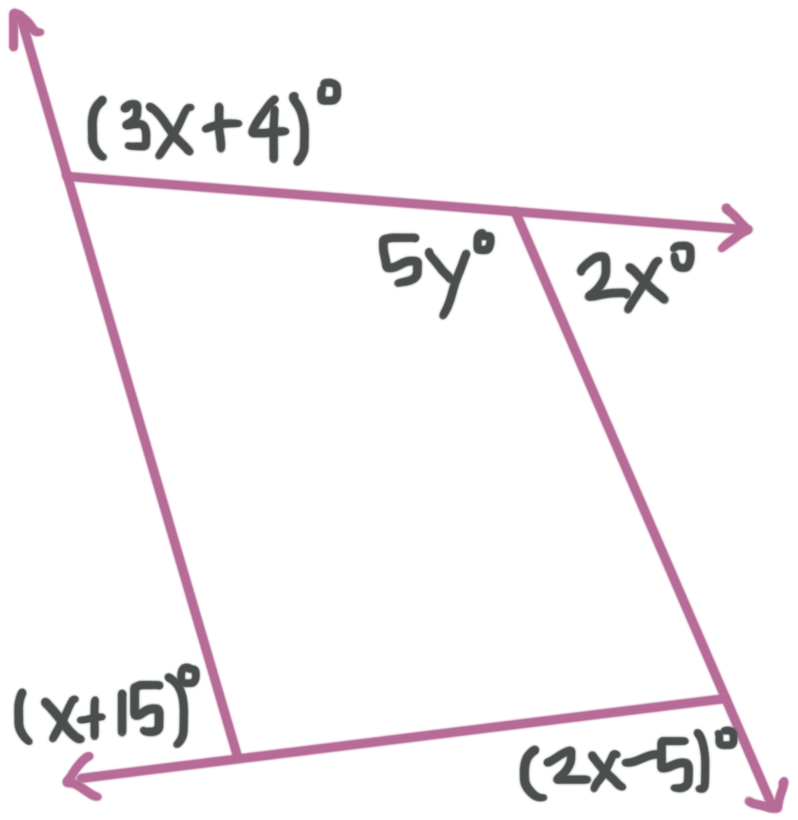
Find the value of ???y???.
The sum of the exterior angles must be ???360{}^\circ???. Therefore, we can say
???3x{}^\circ +4{}^\circ +2x{}^\circ +2x{}^\circ -5{}^\circ +x{}^\circ +15{}^\circ =360{}^\circ???
???3x{}^\circ +2x{}^\circ +2x{}^\circ +x{}^\circ +4{}^\circ -5{}^\circ +15{}^\circ =360{}^\circ???
???8x{}^\circ +14{}^\circ =360{}^\circ???
???8x{}^\circ =346{}^\circ???
???x{}^\circ =43.5{}^\circ???
???5y{}^\circ??? and ???2x{}^\circ??? make a straight line so they are supplementary. Substitute ???43.5{}^\circ??? for ???x??? and solve for ???y???.
???5y{}^\circ +2x{}^\circ =180{}^\circ???
???5y{}^\circ +2(43.25{}^\circ )=180{}^\circ???
???5y{}^\circ +86.5{}^\circ =180{}^\circ???
???5y{}^\circ =93.5{}^\circ???
???y{}^\circ =18.7{}^\circ???
Let’s look at one more example problem.
Example
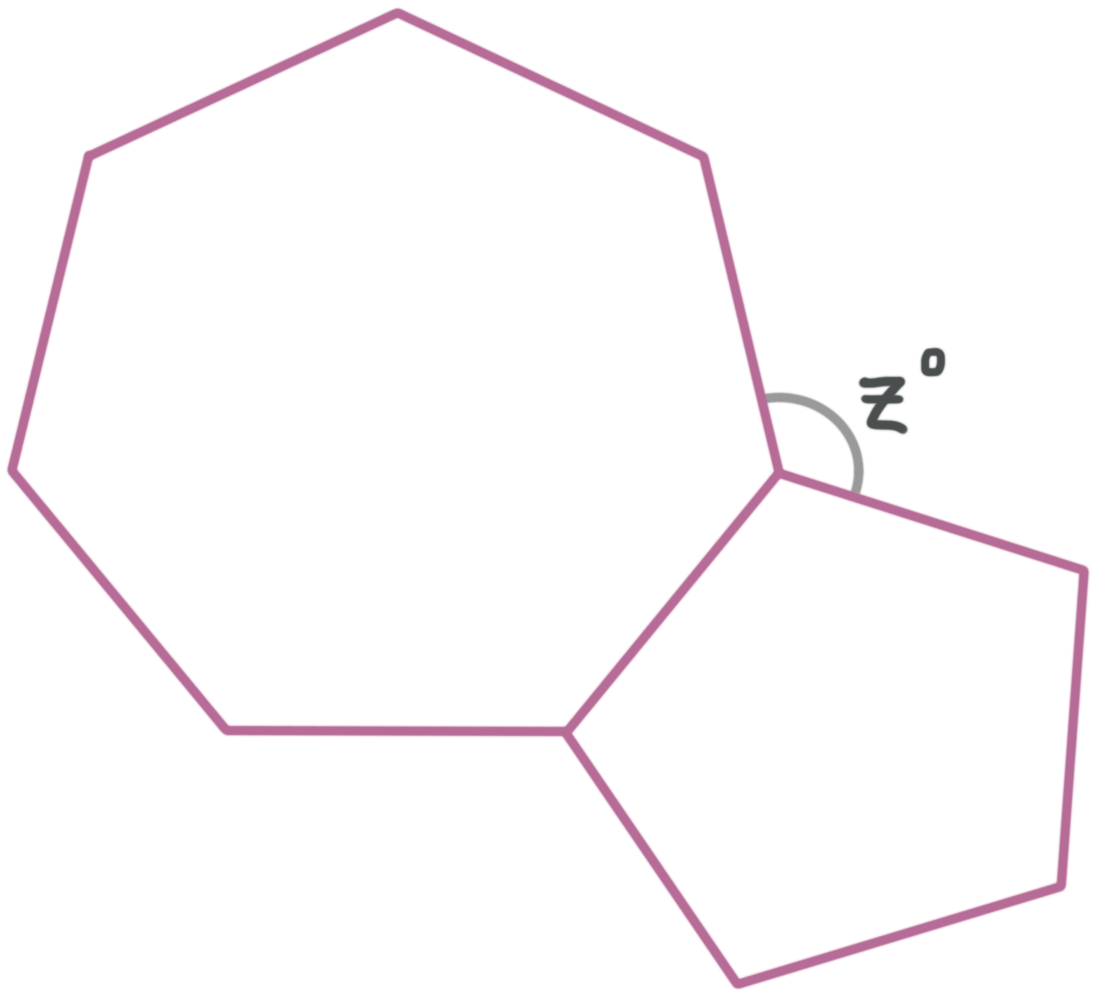
The figure shows a regular heptagon and a regular pentagon. Find the value of ???z??? to the nearest hundredth.
An exterior angle of a regular heptagon has a measure of
???360{}^\circ \div 7\approx 51.43{}^\circ???
An exterior angle of a regular pentagon has a measure of
???360{}^\circ \div 5=72{}^\circ???
Therefore we can say that ???z??? is given by
???z{}^\circ \approx 51.43{}^\circ +72{}^\circ \approx 123.43{}^\circ???