How to graph circles using the center and radius

 
 
Graphing circles blog post.jpeg
 
 
 

Standard form of the equation of a circle

In this lesson we’ll look at how the equation of a circle in standard form relates to its graph.

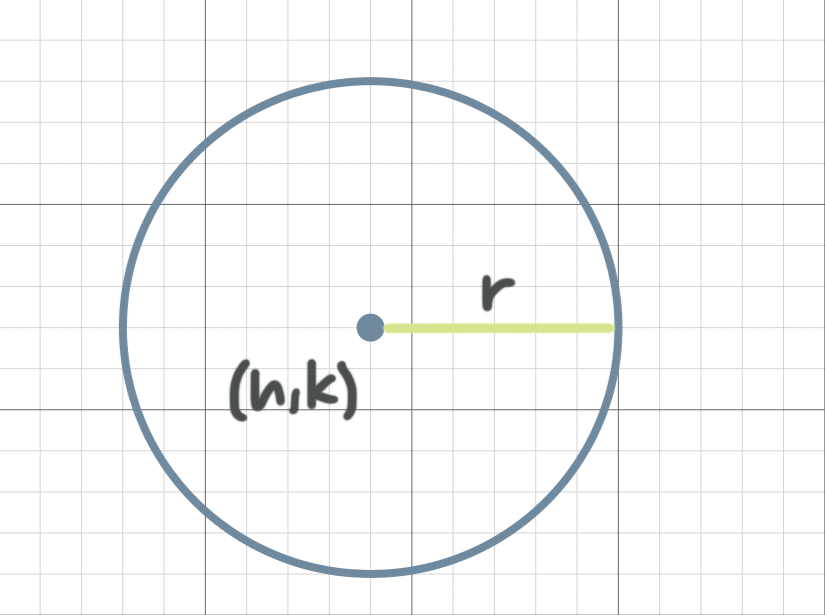
Remember that the equation of a circle in standard form is (x−h)2+(y−k)2=r2(x-h)^2+(y-k)^2=r^2, where (h,k)(h,k) is the center of the circle, and rr is the radius.

Krista King Math.jpg

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

 

As you can see in the image, the center of a circle is a point and the radius of a circle is the distance from the center of the circle to a point on its circumference.

 
center of the circle (h,k) and radius r
 

This means that if you have a graph of a circle, you can write its equation in standard form.

 
 

How to find the equation of a circle and sketch its graph

 
Krista King Math Signup.png
 
Algebra 2 course.png

Take the course

Want to learn more about Algebra 2? I have a step-by-step course for that. :)

 
 
 
 

Finding the equation from the graph of a circle

Example

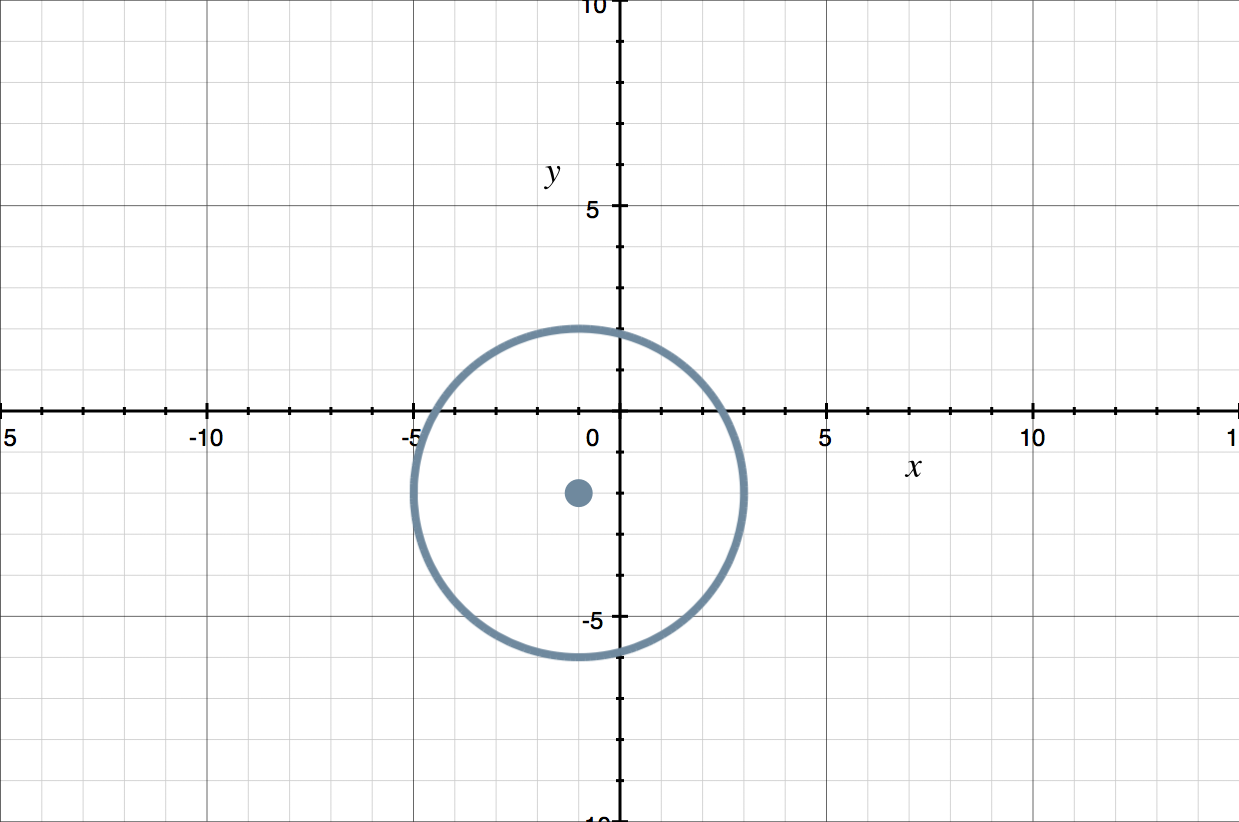
What is the equation of the circle shown in the graph?

find the equation of the circle in the graph


We need to find the equation of a circle in the form (x−h)2+(y−k)2=r2(x-h)^2+(y-k)^2=r^2, which means we need to find the center point and the length of the radius.

Let’s find the center first.

circle sketched in the xy-plane

The center is at (−1,−2)(-1,-2) so h=−1h=-1 and k=−2k=-2. Now let’s count from the center to a point on the circumference to find the length of the radius. The radius is 44, so r=4r=4.

Now let’s plug everything into the standard form of a circle.

(x−h)2+(y−k)2=r2(x-h)^2+(y-k)^2=r^2

(x−(−1))2+(y−(−2))2=42(x-(-1))^2+(y-(-2))^2=4^2

(x+1)2+(y+2)2=16(x+1)^2+(y+2)^2=16

Graphing circles for Algebra 2.jpg

This means that if you have a graph of a circle, you can write its equation in standard form.

Example

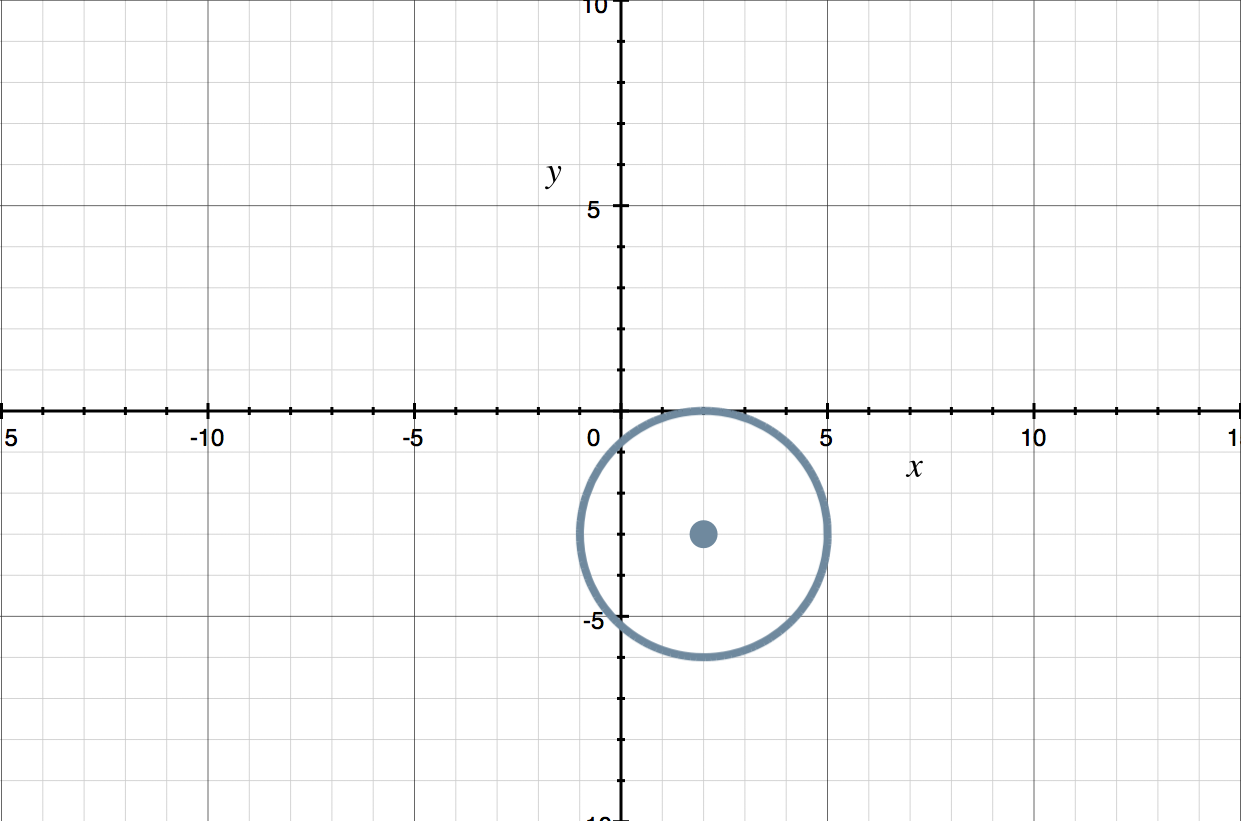
Graph the circle.

(x−2)2+(y+3)2=9(x-2)^2+(y+3)^2=9

In order to graph a circle, we need to know its center and radius. In standard form, the equation of a circle is

(x−h)2+(y−k)2=r2(x-h)^2+(y-k)^2=r^2

where (h,k)(h,k) is the center and rr is the radius. Let’s go ahead and write out the equation as

(x−2)2+(y+3)2=9(x-2)^2+(y+3)^2=9

(x−2)2+(y+3)2=32(x-2)^2+(y+3)^2=3^2

Now we can see that the center is (h,k)=(2,−3)(h,k)=(2,-3) and the radius is r=3r=3. Let’s graph the circle, starting with the center point.

first graph the center point of the circle

Since the radius is r=3r=3, we’ll count three units in all directions from the center point, or we can use a compass to draw a more perfect circle.

sketch the radius from the center of the circle
 
Krista King.png
 

Get access to the complete Algebra 2 course

 
Learn mathKrista Kingmath, learn online, online course, online math, algebra, algebra 2, algebra ii, circles, graphing circles, radius of the circle, center, radius, standard equation of the circle, standard form of the equation of a circle, equation of the circle, circle equation, center of the circle