How to graph log functions and their transformations
Seeing exponential and log functions as inverses of one another
Previously, we talked about the fact that exponential and logarithmic functions are inverses of one another. This is implied by the general log rule,
???a^x=y\quad\text{implies}\quad\log_a{(y)}=x???
which allows us to convert back and forth between the exponential function (on the left) and the log function (on the right).
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Remember that this is also true for natural logs, as
???e^x=y\quad\text{implies}\quad\log_e{(y)}=x???
And in the very last section, we just talked about the graphs of exponential functions, including how to graph transformations of exponential functions.
Because exponential and logarithmic functions are inverses of one another, if we have the graph of the exponential function, we can find the corresponding log function simply by reflecting the graph over the line ???y=x???, or by flipping the ???x???- and ???y???-values in all coordinate points.
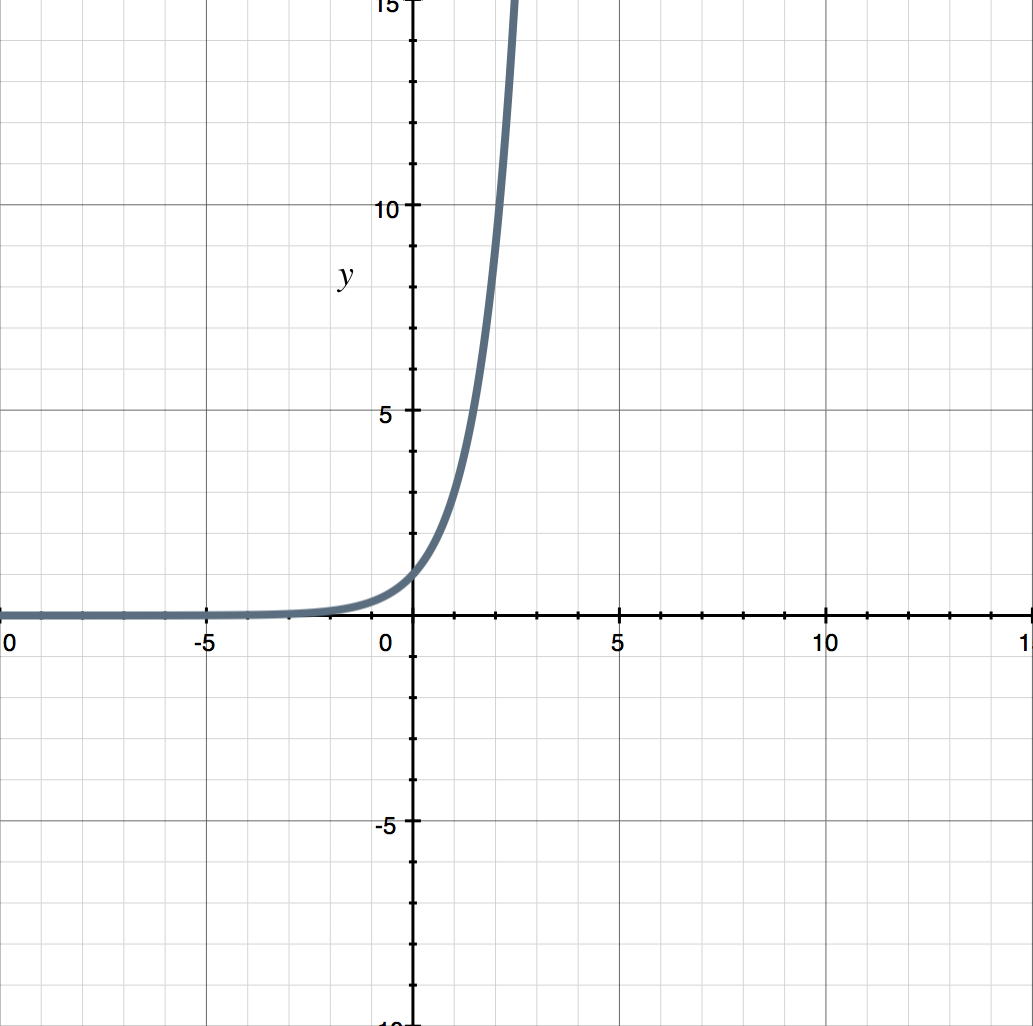
Let’s use some graphs from the previous section to illustrate what we mean. For instance, we already know that the graph of the exponential function ???y=3^x??? is
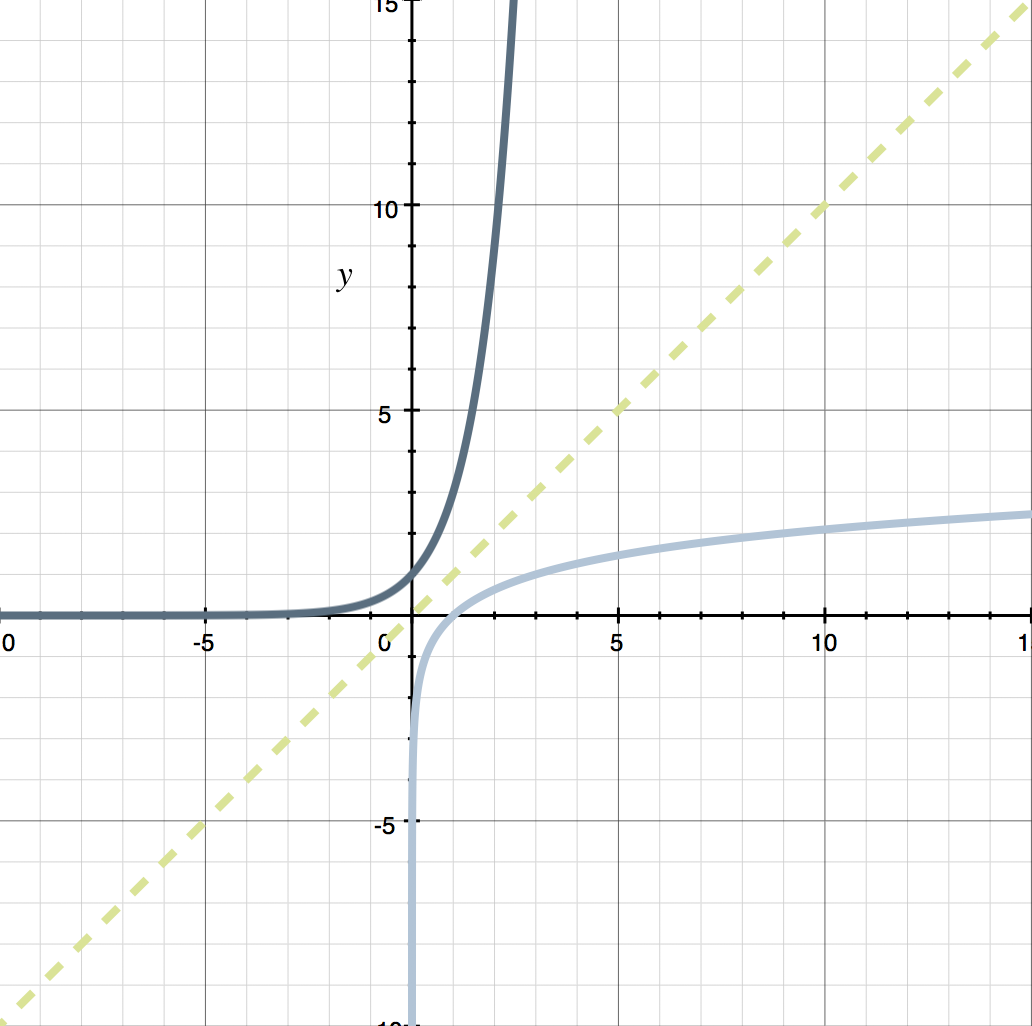
Let’s now find the inverse of this exponential function. Functions which are inverses of each other simply have their ???x???- and ???y???-values flipped, which means that the inverse of ???y=3^x??? can simply be given by ???x=3^y??? (the same equation, just with the ???x??? and ???y??? swapped). If we sketch ???x=3^y???, we see that we get the mirror image of ???y=3^x???, reflected over the line ???y=x???.
The interesting thing is that, if we put this inverse function ???x=3^y??? through the general log rule, and put it into its logarithmic form, we get
???x=3^y\quad\text{implies}\quad y=\log_3{x}???
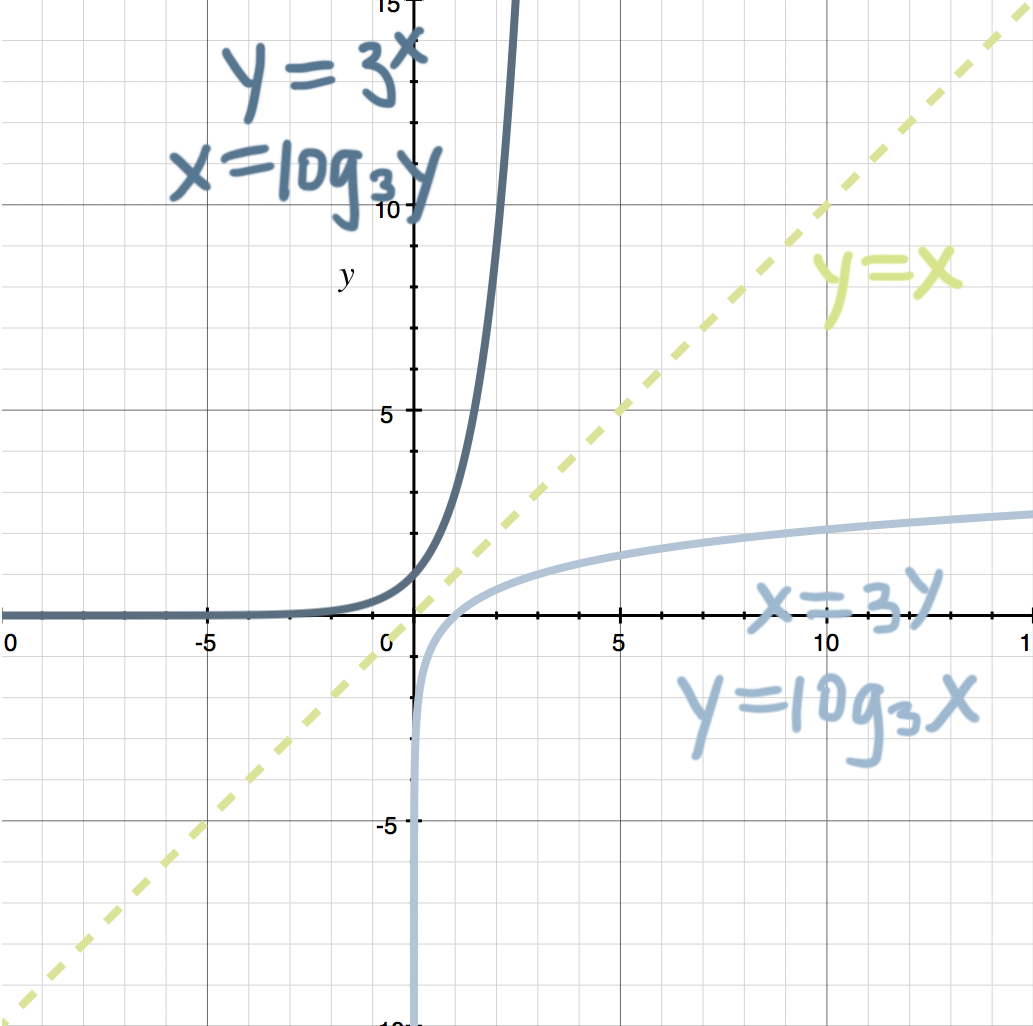
Therefore, we can actually say that ???y=3^x??? and ???y=\log_3{x}??? are inverses of one another. Similarly, ???x=3^y??? and ???x=\log_3{y}??? are inverse of one another. Let’s show both the exponential and logarithmic expression of both functions, and how they are inverses of other, reflected over ???y=x???.
Let’s walk through a couple of examples of graphing logarithmic functions, keeping in mind that we can always use the general log rule to convert them to their exponential form, and then graph them in their exponential form using the steps we used in the last section.
How to graph logarithmic functions, and transformations of log functions (shifts, reflections, etc.)
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Graphing a transformed logarithmic function step-by-step
Example
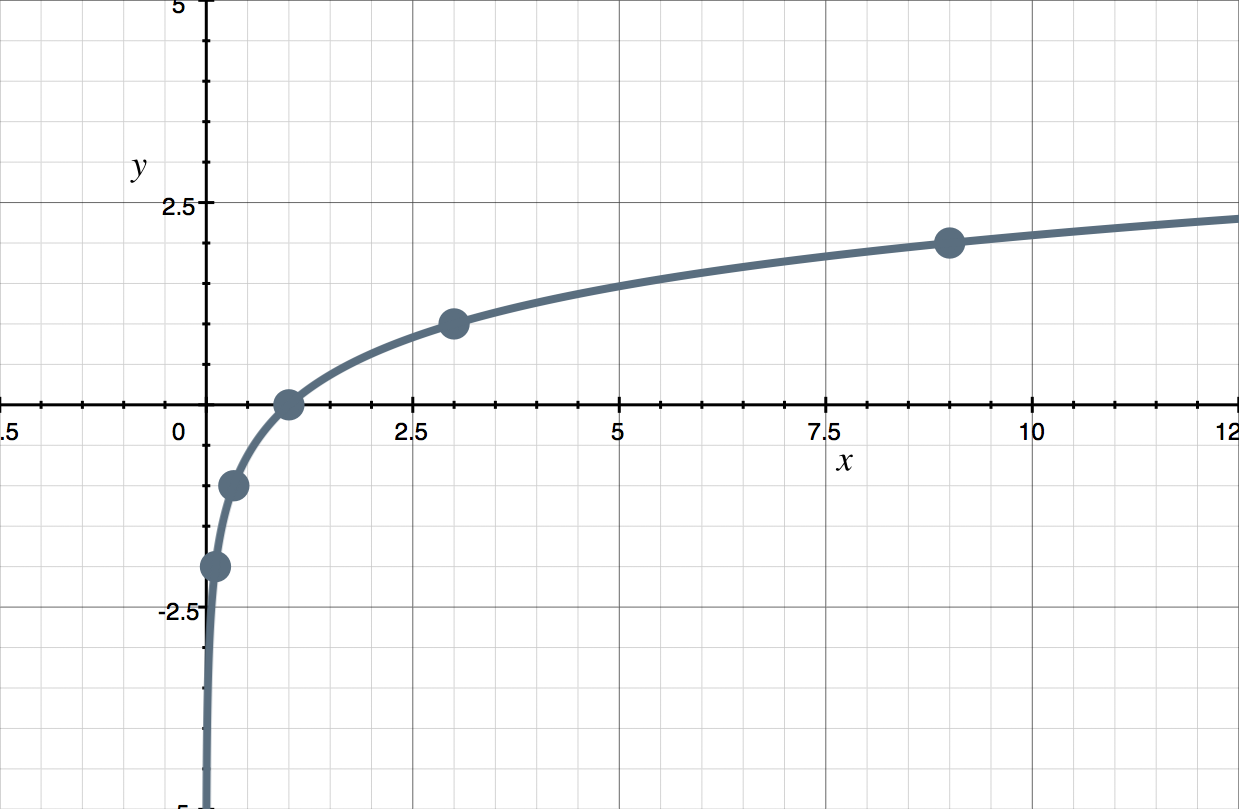
Graph the logarithmic function.
???y=\log_3{x}???
There are several ways to go about this. First, we could use the general rule for logs to convert the logarithmic equation into an exponential equation. ???y=\log_3{x}??? becomes ???x=3^y???. Then we can follow the steps from the previous section, starting with plugging in ???y=100??? and ???y=-100???.
For ???y=100???:
???x=3^{100}???
???x=\text{very large positive number}???
???x=\infty???
For ???y=-100???:
???x=3^{-100}???
???x=\frac{1}{3^{100}}???
???x=\frac{1}{\text{very large positive number}}???
???x=\frac{1}{\infty}???
???x=0???
This basically allowed us to evaluate end behavior, and we’ve learned that the function has a vertical asymptote at ???x=0???, and heads up toward ???\infty??? as ???y??? gets very large.
We’ll plug in a few simple-to-evaluate values for ???y???.
For???y=-1??? :
???x=3^{-1}???
???x=\frac13???
For ???y=0???:
???x=3^0???
???x=1???
For ???y=1???:
???x=3^1???
???x=3???
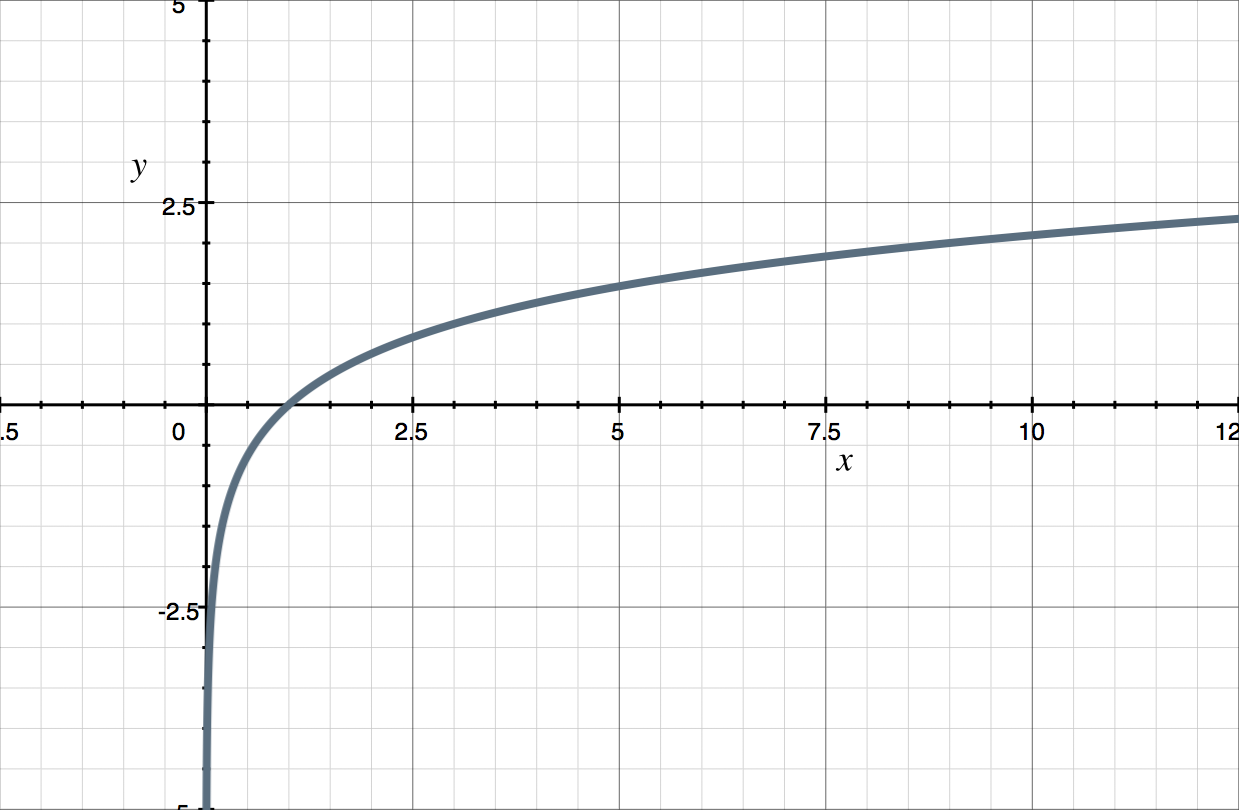
If we plot these values, along with the vertical asymptote ???x=0???, and then connect the points, we get the graph of ???x=3^y???.
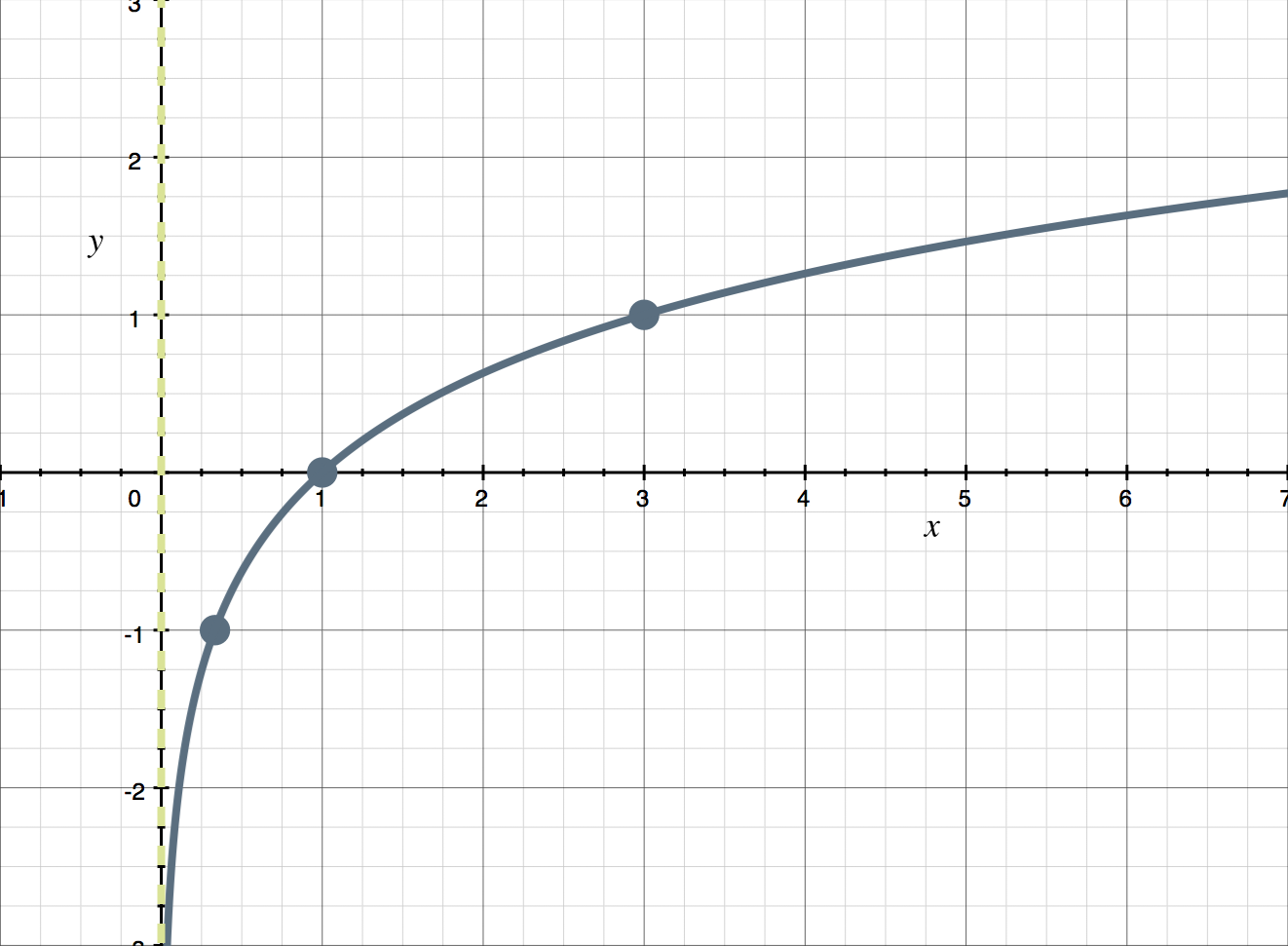
We can also plot the log function using a table of points. Since ???y=\log_3{x}??? corresponds to ???x=3^y???, then we can find coordinate points that satisfy this exponential function. It’ll be easier for us to plug in values for ???y???, and see which ???x???-values come out of the equation. For instance, if we plug ???y=0??? into ???x=3^y???, we get ???x=1???.
Let’s fill out the rest of the chart with a few other easy-to-calculate values. It doesn’t matter which values we pick, because we’re just trying to get a few points that we can plot on the graph of the logarithmic function.
With ???5??? points that satisfy the equation, we should be able to pretty easily sketch the graph.
Just like exponential functions in the previous section, we can also graph transformations of logarithmic functions.
Because exponential and logarithmic functions are inverses of one another, if we have the graph of the exponential function, we can find the corresponding log function simply by reflecting the graph over the line y=x.
Example
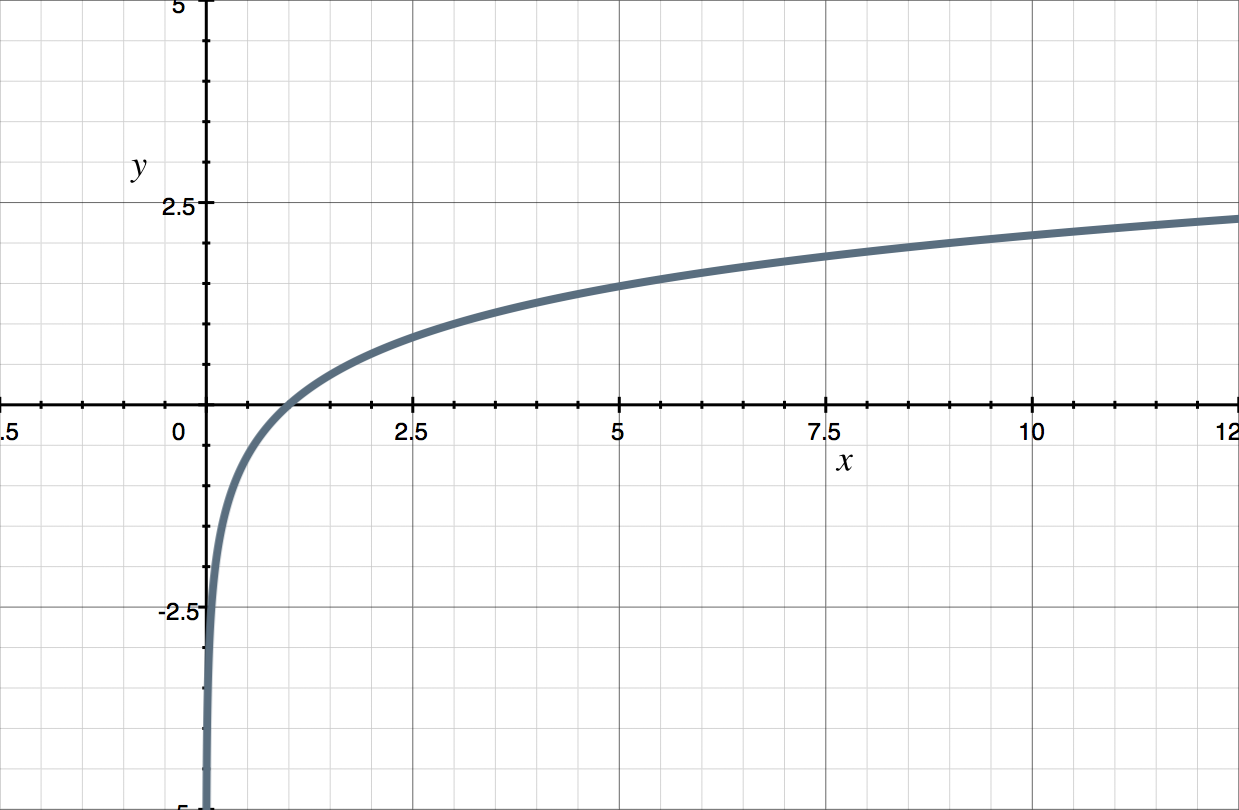
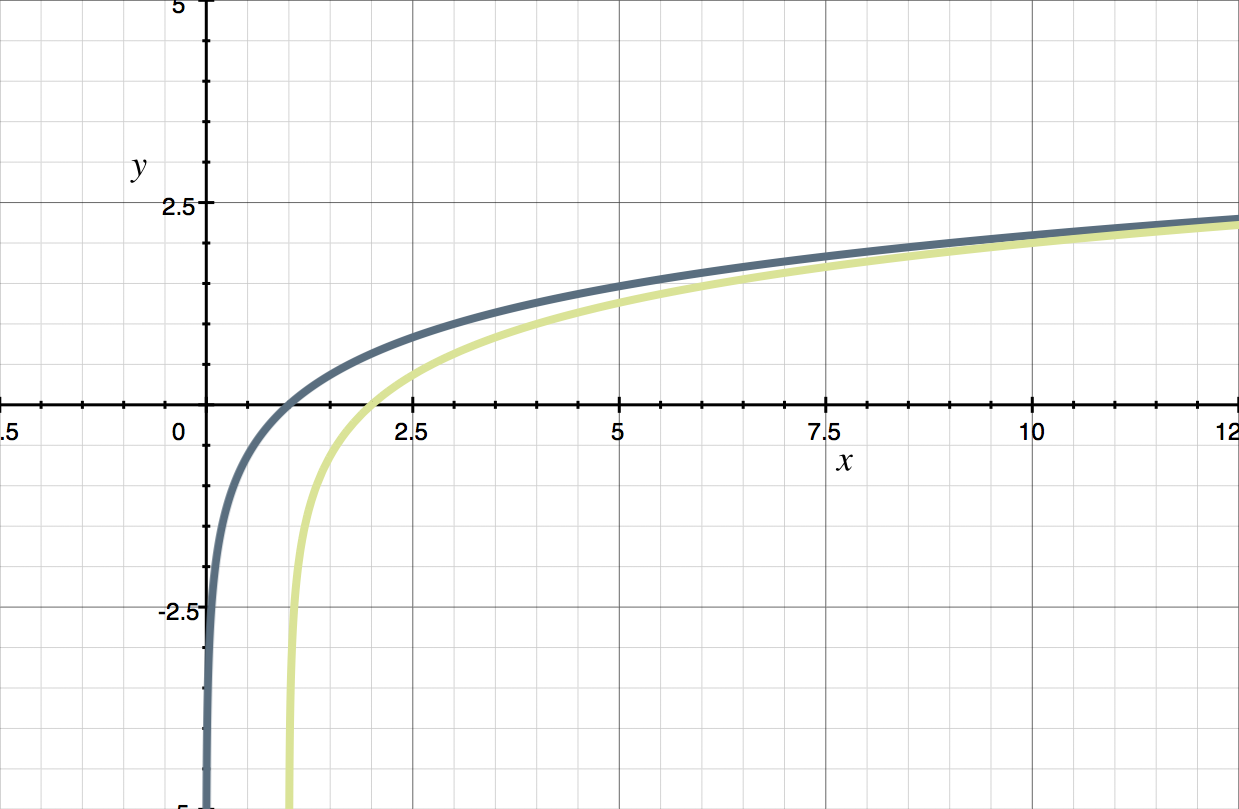
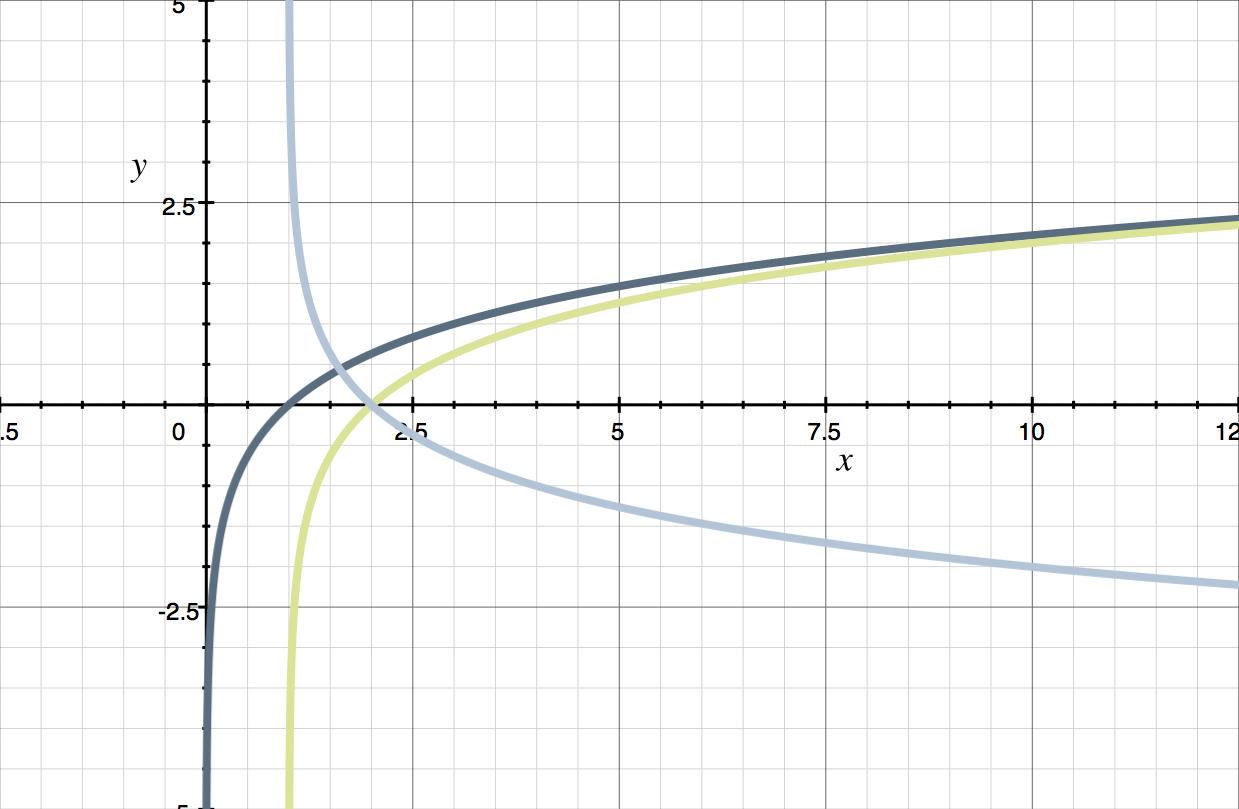
The graph of ???y=\log_3{x}??? is given. Use the graph to sketch a graph for ???y=-\log_3{(x-1)}???.
Both functions are based on the standard ???y=\log_3{x}??? function. The function ???y=-\log_3{(x-1)}??? has simply undergone a couple of transformations. We want to break up the transformations so that we show each transformation in its own step.
[1] ???y=\log_3{x}???
[2] ???y=\log_3{(x-1)}???
[3] ???y=-\log_3{(x-1)}???
We were given the graph of [1] ???y=\log_3{x}???.
If we change the ???x??? into ???x-1???, that means we’re shifting the graph over one unit to the right. If you’re not sure about this, try plugging a few points into ???y=\log_3{(x-1)}???. If we plot [2] ???y=\log_3{(x-1)}??? on the same set of axes, we get
Multiplying by ???-1??? means that each value of ???y=\log_3{(x-1)}??? gets multiplied by ???-1???, which means that the value will get flipped over the ???y???-axis.
To summarize, we started with ???y=\log_3{x}??? and its graph, and were able to undergo one transformation at a time,
[1] ???y=\log_3{x}???
[2] ???y=\log_3{(x-1)}???
[3] ???y=-\log_3{(x-1)}???
to eventually get to the graph of ???y=-\log_3{(x-1)}???.