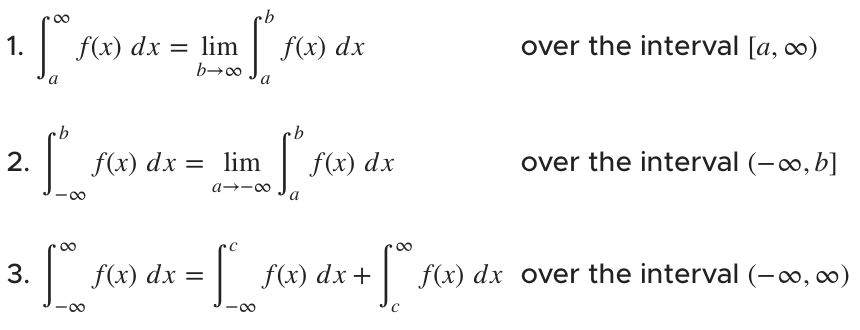How to solve improper integrals
What are improper integrals?
Improper integrals are just like definite integrals, except that the lower and/or upper limit of integration is infinite.
Remember that a definite integral is an integral that we evaluate over a certain interval. An improper integral is just a definite integral where one end of the interval is ???\pm\infty???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The formulas we use to deal with improper integrals are
If the limit in case ???1??? or ???2??? exists (if it generates a real number answer), we say that it converges. If the limit in case ???1??? or ???2??? does not exist, we say that it diverges. This means the answer isn’t a real number (the answer might be ???\pm\infty???).
In case ???3???, the equation will diverge if either of the integrals on the right-hand side diverge. This means that in order for case ???3??? to converge, both integrals on the right-hand side must have real-number answers.
What makes an integral improper?
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
How to solve a Case 1 improper integral
Example
Evaluate the improper integral.
???\int^\infty_0\frac{1}{x^2+1}\ dx???
This integral is like case ???1???, so we use the rule to get
???\int^\infty_af(x)\ dx=\lim_{b\to\infty}\int^b_af(x)\ dx???
???\int^\infty_0\frac{1}{x^2+1}\ dx=\lim_{b\to\infty}\int^b_0\frac{1}{x^2+1}dx???
Integrating, we get
???\lim_{b\to\infty}\arctan{x}\big|^b_0???
Evaluating over the interval ???[0,b]???, we get
???\lim_{b\to\infty}\left[\arctan{(b)}-\arctan{(0)}\right]???
???\arctan{(\infty)}???
???\frac{\pi}{2}???
In this case, since we get a real number answer, we know that our integral converges.
When infinity occurs as part of the interval, or when one end of the interval approaches infinity, we say that the equation has an infinite discontinuity. In other words, that the equation has an asymptote in the interval or at one end of the interval.
For improper integrals that are infinitely discontinuous somewhere in the interval, we use the following formulas.
If the limit in case ???4??? or ???5??? exists (if it generates a real-number answer), we say that it converges. If the limit in case ???4??? or ???5??? does not exist, we say that it diverges. This means the answer isn’t a real number (the answer might be ???\pm\infty???).
In case ???6???, the equation will diverge if either integral on the right-hand side diverges. This means that in order for case ???6??? to converge, both integrals on the right-hand side must have real-number answers.
When infinity occurs as part of the interval, or when one end of the interval approaches infinity, we say that the equation has an infinite discontinuity.
How to solve a Case 5 improper integral
Example
Evaluate the improper integral.
???\int^2_{0}\frac{1}{x^3}\ dx???
This integral is like case ???5???, so we use the rule to get
???\int^b_af(x)\ dx=\lim_{c\to{a^+}}\int^b_cf(x)\ dx???
???\int^2_{0}\frac{1}{x^3}\ dx=\lim_{c\to{0^+}}\int^2_c\frac{1}{x^3}\ dx???
Integrating, we get
???\lim_{c\to{0^+}}\left(-\frac{1}{2x^2}\right)\bigg|^2_c???
Evaluating over the interval ???[c,2]???, we get
???\lim_{c\to{0^+}}\left(-\frac{1}{2(2)^2}+\frac{1}{2c^2}\right)???
???\lim_{c\to{0^+}}\left(-\frac{1}{8}+\frac{1}{2c^2}\right)???
???\infty???
In this case, since we get an infinite answer, we know that our integral diverges.