Inscribed angles of circles
How can we build inscribed angles and their intercepted arcs?
In this lesson we’ll look at inscribed angles of circles and how they’re related to arcs, called intercepted arcs.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Chord of a circle
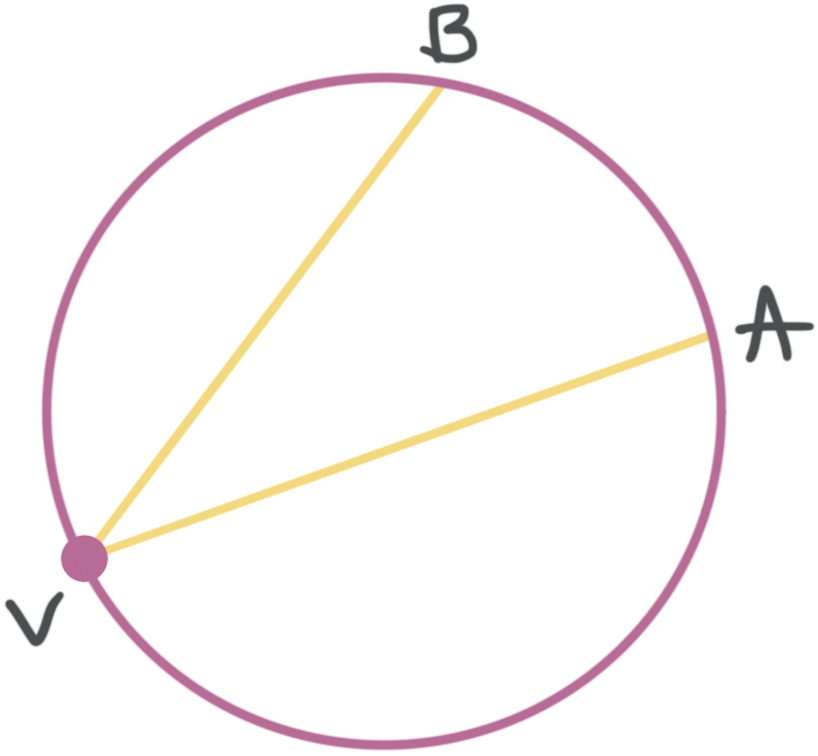
A chord is a straight line segment that has endpoints on the circumference of the circle. The diameter of a circle is a special type of chord that passes through the circle’s center. The yellow line is an example of a chord.
Inscribed angle
An inscribed angle is formed by two chords. These chords share the vertex of an angle. The arc that touches the endpoints of the chords is called the intercepted arc.
Angle ???AVB??? is an inscribed angle and arc ???AB??? is the intercepted arc.
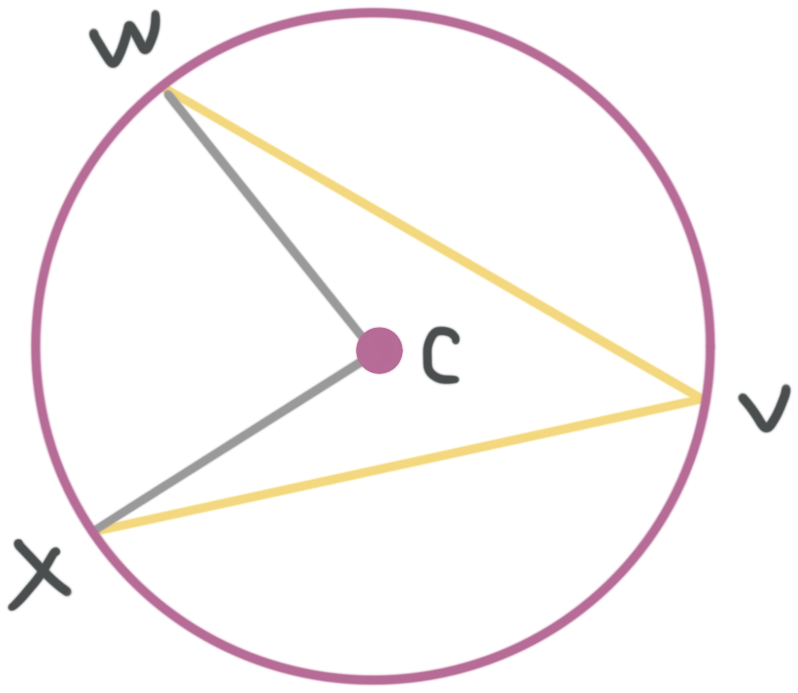
Measures of inscribed angles, central angles and intercepted arcs
The measure of an intercepted arc is equal to the measure of its central angle.
The measure of an inscribed angle is equal to half the measure of the central angle that goes with the intercepted arc.
The measure of an inscribed angle is equal to half the measure of its intercepted arc.
???m\text{ arc }{WX}=m\angle WCX???
???\frac{1}{2}m\angle WCX=m\angle WVX???
???\frac{1}{2}m\text{ arc }{WX}=m\angle WVX???
We can do some algebra to show that the following is also true.
???m\angle WCX=\frac{1}{2}m\text{ arc }{WX}=\angle WCX=2m\angle WVX???
Calculating measurements of inscribed angles in circles
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Calculating measures of inscribed angles
Example
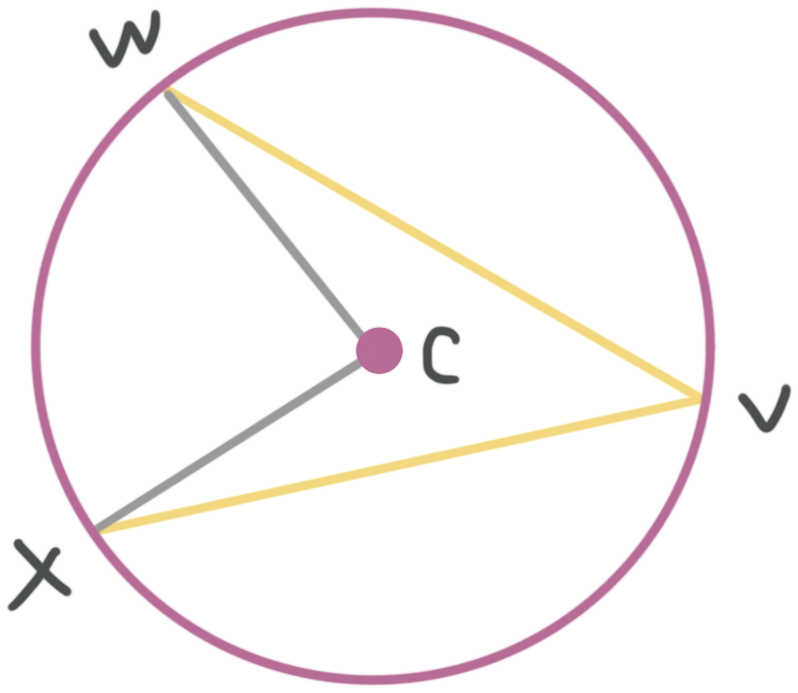
Find the measure of the inscribed angle ???WVX??? if ???m\angle WCX=88^\circ???.
???\angle WCX??? is the central angle for the intercepted arc ???WX???. This means the inscribed angle measures half of the measure of ???\angle WCX???. We know
???\frac{1}{2}m\angle WCX=m\angle WVX???
and
???m\angle WCX=88^\circ???
So
???\frac{1}{2}(88^\circ )=m\angle WVX???
???44^\circ =m\angle WVX???
Let’s do a problem with a few more steps.
An inscribed angle is formed by two chords. These chords share the vertex of an angle. The arc that touches the endpoints of the chords is called the intercepted arc.
Example
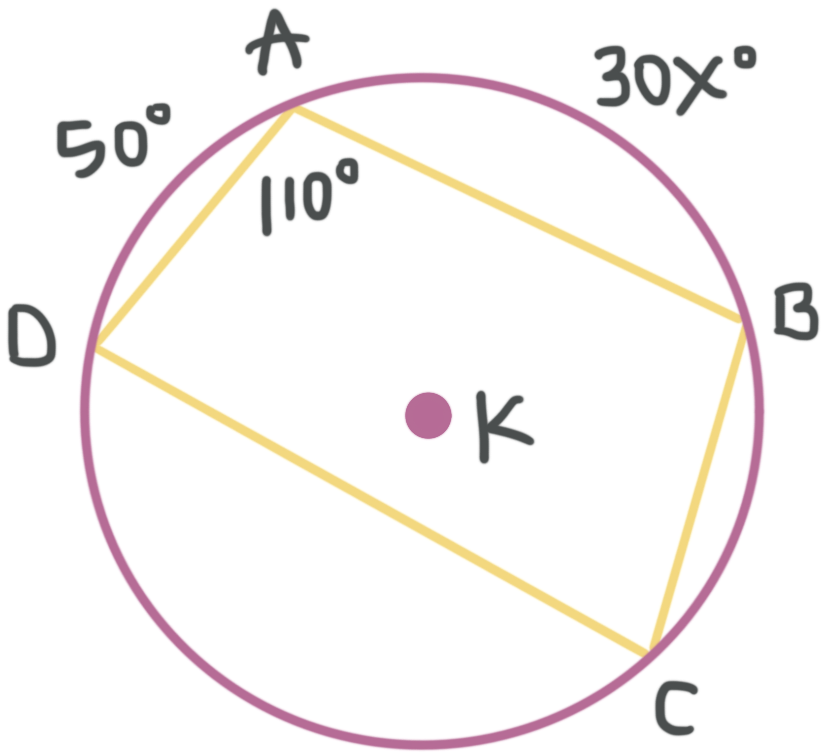
Solve for ???x???.
The full circle is ???360^\circ???. If we can find the measure of arc ???DB???, we can set up an equation to solve for ???x???, because ???m\text{ arc }{DB}+m\text{ arc }{BA}+m\text{ arc }{AD}=360^\circ???, and we know that ???m\text{ arc }{BA}=30x??? and ???m\text{ arc }{AD}=50^\circ???.
From the diagram we can see that ???m\angle DAB=110{}^\circ???. The intercepted arc that belongs to this angle is arc ???DB???. The intercepted arc has a measure of twice the inscribed angle.
???m\text{ arc }{DB}=2m\angle DAB=2(110^\circ )???
???m\text{ arc }{DB}=220^\circ???
Now we can use the equation we wrote earlier to solve for ???x???.
???m\text{ arc }{DB}+m\text{ arc }{BA}+m\text{ arc }{AD}=360^\circ???
???220^\circ +30x+50^\circ =360^\circ???
???270^\circ +30x=360^\circ???
???30x=90^\circ???
???x=3^\circ???