How to use the Intersecting chord theorem

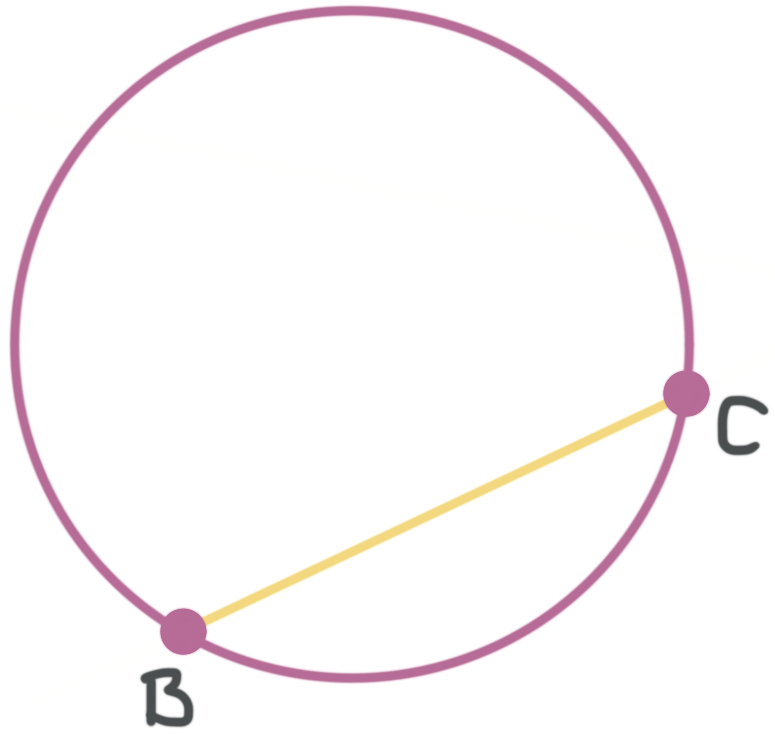
A chord is a line segment that has both of its endpoints on the edge of the circle

A chord of a circle is a line segment that has both of its endpoints on the circumference of a circle.

$\overline{BC}$ is an example of a chord.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Intersecting chord theorem

The intersecting chord theorem states that the products of chord segments are always equal. For instance, consider chords $\overline{BD}$ and $\overline{EF}$,

then the intersecting chord theorem says that

$BC\cdot CD=EC\cdot CF$

Solving for chord length using the intersecting chord theorem

---

Take the course

Want to learn more about Geoemtry? I have a step-by-step course for that. :)

---

Apply the intersecting chord theorem to find the length of the chords

Example

Find the value of $x$ in the figure.

The products of the chord segments are equal. So we can set up an equation.

$5(5x+5)=5(3x+12)$

$25x+25=15x+60$

$10x=35$

$x=3.5$

The intersecting chord theorem states that the products of chord segments are always equal.

Example

Find the length of the each chord.

First we need to find the value of $x$, and then use that to find the length of the chords. The products of the chord segments are equal, so

$12(x-4)=9(x-2)$

$12x-48=9x-18$

$3x=30$

$x=10$

Now we can find the length of each chord. One chord has a length of

$12+x-4$

$12+10-4$

$18$

The other chord has a length of

$x-2+9$

$10-2+9$

$17$

The chords have lengths of $17$ and $18$.

---

Get access to the complete Geometry course

---