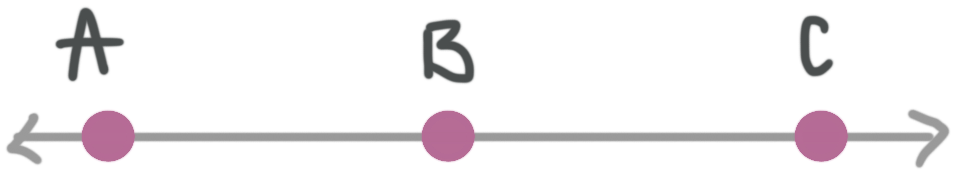Finding length and midpoint of a line segment
What is the midpoint of a line segment?
In this lesson we’ll look at how to find the length of a line segment algebraically when we’re given information and measurements about parts of the line segment.
Remember that a line segment is a finite piece of a line, named by its endpoints. For instance, the line segment ???\overline{AB}??? might look like this:
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Line segments and distance
The distance between two points on a line segment is called the length of the segment. We usually use the same symbol for the length of the line segment that we use for the segment itself. So ???\overline{AB}??? could be used to represent the segment itself, but also the length of the segment.
In this example, the distance between points ???A??? and ???B??? is
???\overline{AB}=|3-(-2)|???
???\overline{AB}=|3+2|???
???\overline{AB}=|5|???
???\overline{AB}=5???
In this example, you could also count from ???A??? to ???B??? and get a distance of ???5???. As you can see, sometimes it may be helpful to draw a number line in order to visualize the length of a line segment.
Finding the length of a line segment, and then its midpoint
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Using a number line to solve midpoint problems
Example
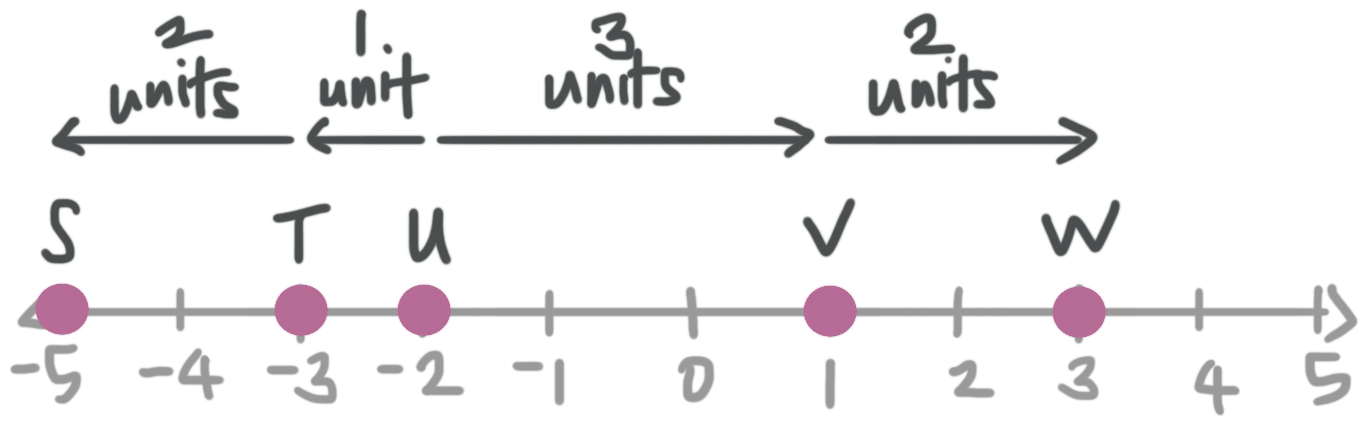
Points ???S???, ???T???, ???U???, ???V???, and ???W??? lie in order on a number line. Point ???U??? is at ???-2???. Where are the rest of the points located?
???\overline{ST}=2???
???\overline{TU}=1???
???\overline{UV}=3???
???\overline{VW}=2???
If we plot point ???U??? at ???-2???, then ???S???, ???T???, ???U???, ???V???, and ???W??? must be plotted this way:
We know point ???U??? is on ???-2??? and ???\overline{TU}=1???. This lets us locate point ???T??? at ???-3???. Now we can use ???\overline{ST}=2??? to find that ???S=-5??? and ???\overline{UV}=3??? to find that ???V=1???. Now we can locate point ???W??? by using ???\overline{VW}=2???, so ???W=3???.
Let’s look at another example.
The distance between two points on a line segment is called the length of the segment.
Example
Find ???\overline{AB}???, if ???\overline{AC}=12??? and ???\overline{BC}=7???.
We know that ???\overline{AC}=12??? and ???\overline{BC}=7???. From the diagram, we also know that ???\overline{AB}??? is part of ???\overline{AC}???.
We can see that ???\overline{AC}-\overline{BC}=\overline{AB}???, so we have ???\overline{AB}=12-7=5???.
Let’s look at one last example.
Example
The locations of four points on a number line are ???A=2???, ???B=4???, ???C=-3???, and ???D=-6???. What is the value of ???\overline{AB}+\overline{CD}????
We can draw a number line to help solve the problem.
Now we can see that ???\overline{AB}=|4-2|=2??? units and ???\overline{CD}=|-3-(-6)|=3??? units. So ???\overline{AB}+\overline{CD}=2 + 3 = 5??? units.