Measures of parallelograms, including angles, sides, and diagonals

Defining all the measures of a parallelogram

A parallelogram is a quadrilateral that has opposite sides that are parallel.

The parallel sides let you know a lot about a parallelogram.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Here are the special properties of parallelograms:

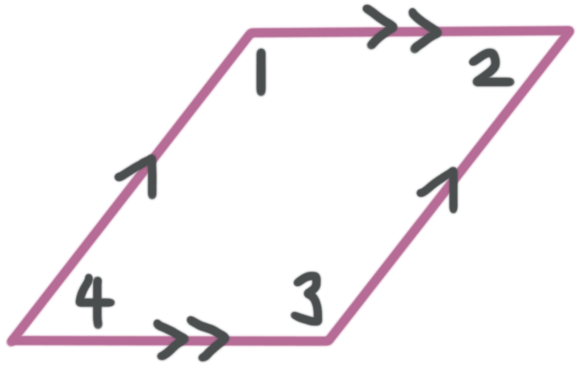
Parallelogram

Two pairs of opposite parallel sides

Opposite sides are equal lengths

Opposite angles are congruent

$m\angle 1=m\angle 3$

$m\angle 2=m\angle 4$

Consecutive angles are supplementary

$m\angle 1+m\angle 2=180^\circ$

$m\angle 2+m\angle 3=180^\circ$

$m\angle 3+m\angle 4=180^\circ$

$m\angle 4+m\angle 1=180^\circ$

Diagonals bisect each other (cut each other in half)

How to solve for every measure of a parallelogram, including angles, side lengths, and the lengths of diagonals

---

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

---

Finding the measure of a interior angle of a parallelogram

Example

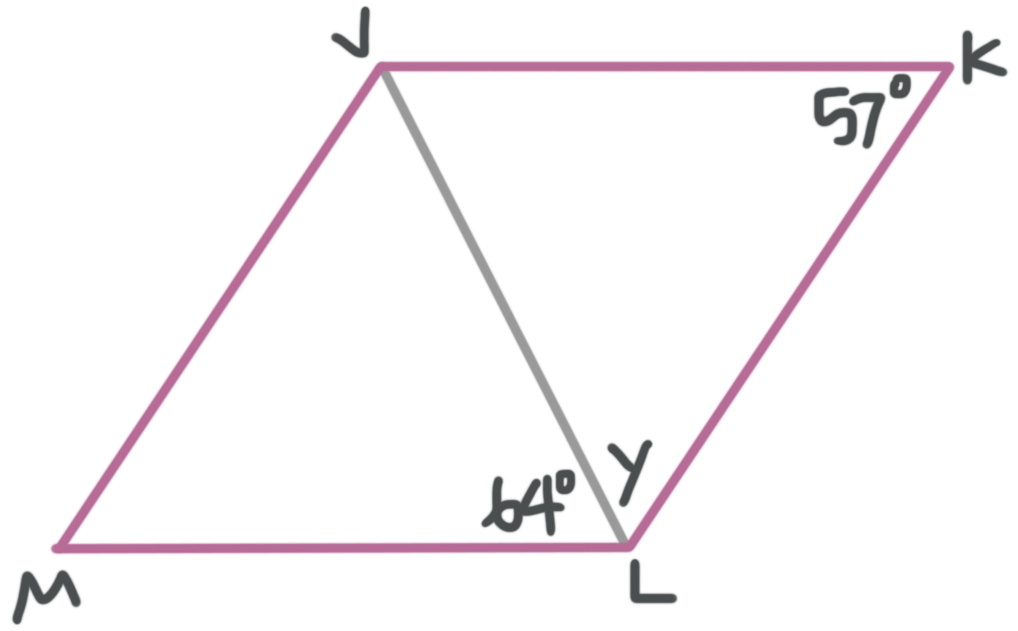
Find the measure of angle $y$, given $JKLM$ is a parallelogram.

Opposite angles of parallelograms are congruent, so

$m\angle JML=m\angle JKL=57^\circ$

Now we can use the fact that opposite sides of a parallelogram are parallel to state that $JK\parallel ML$. This means that the diagonal $JL$ of the parallelogram is also a transversal of these two parallel lines. This means that $\angle KLJ$ and $\angle MJL$ are alternate interior angles. Alternate interior angle pairs are congruent, so $m\angle KLJ=m\angle MJL=y$.

The measures of the three interior angles of a triangle add up to $180^\circ$, so we can set up an equation for the sum of the interior angles of $\triangle JML$ and solve for $y$.

$y+57^\circ+64^\circ=180^\circ$

$y=59^\circ$

A parallelogram is a quadrilateral that has opposite sides that are parallel.

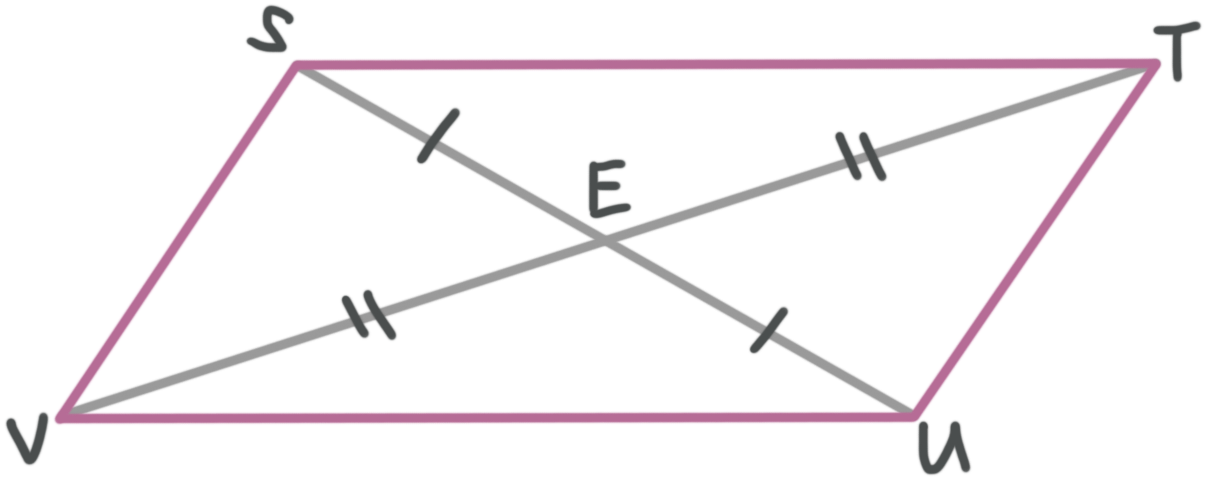
Example

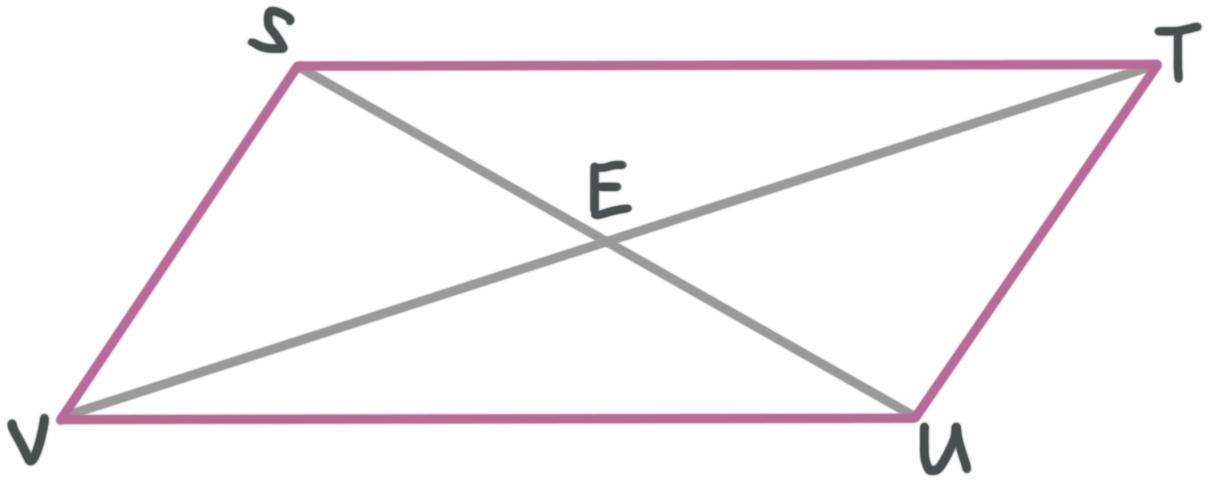
If $STUV$ is a parallelogram, and if $VT=4n+34$ and $VE=7n-3$, what is the length of $ET$?

We know that the diagonals of a parallelogram bisect each other. Let’s add this information into the diagram.

Now we can see the relationships we need. Because the diagonals bisect, $VE=ET$ and $VE=(1/2)VT$. We can use what we know to find the length of $VE$ and then we’ll know the length of $ET$ as well.

$VE=\frac{1}{2}VT$

$7n-3=\frac{1}{2}(4n+34)$

$7n-3=2n+17$

$5n=20$

$n=4$

Now we can substitute back in to find the length of $VE$, which is equal to the length of $ET$.

$VE=ET=7n-3$

$VE=ET=7(4)-3$

$VE=ET=25$

---

Get access to the complete Geometry course

---