One-to-one functions and the horizontal line test
What is a one-to-one function?
In this section we’ll talk about how to determine whether a graph represents a one-to-one function.
If a relation is a function, then it has exactly one ???y???-value for each ???x???-value. If a function is one-to-one, it also has exactly one ???x???-value for each ???y???-value.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The reason we care about one-to-one functions is because only a one-to-one function has an inverse. If the function is not one-to-one, then some restrictions might be needed on the domain of the function to make it invertible.
The first way we’ll look at whether or not a function is one-to-one is using the Horizontal Line Test.
One-to-one functions with the horizontal line test
Remember that we’ve already talked about the Vertical Line Test, which is a test we use to tell us whether or not a graph represents a function. Any function passing the Vertical Line Test can only have one unique output value ???y??? for any single input value ???x???.
In the same way that the Vertical Line Test tells us whether or not a graph is a function, the Horizontal Line Test tells us whether or not a function is one-to-one.
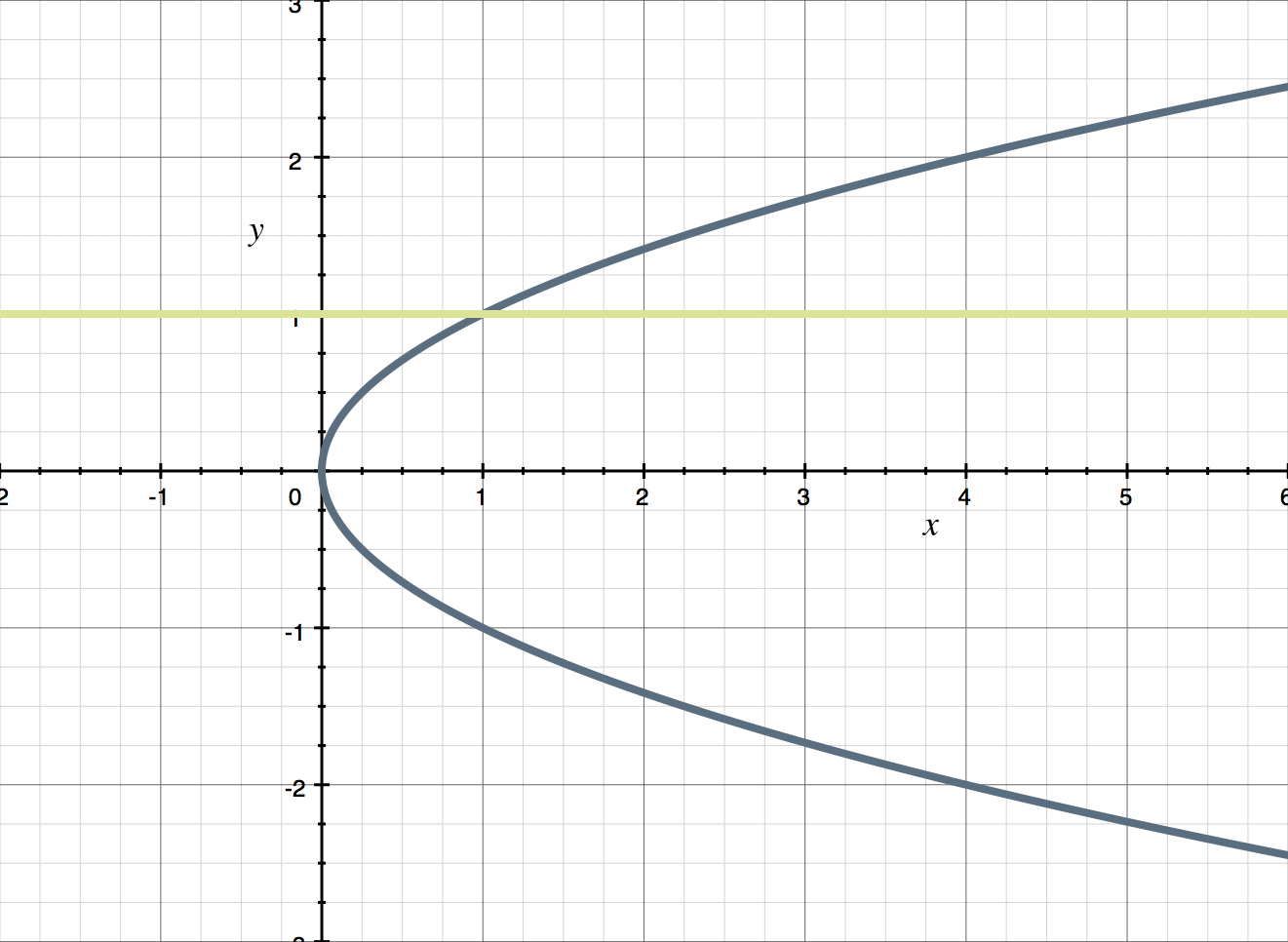
The graph below passes the Horizontal Line Test because a horizontal line cannot intersect it more than once.
Basically, the Horizontal Line Test says that no ???y???-value corresponds to two different ???x??? values. If a function passes the Horizontal Line Test, then no horizontal line will cross the graph more than once, and the graph is said to be one-to-one.
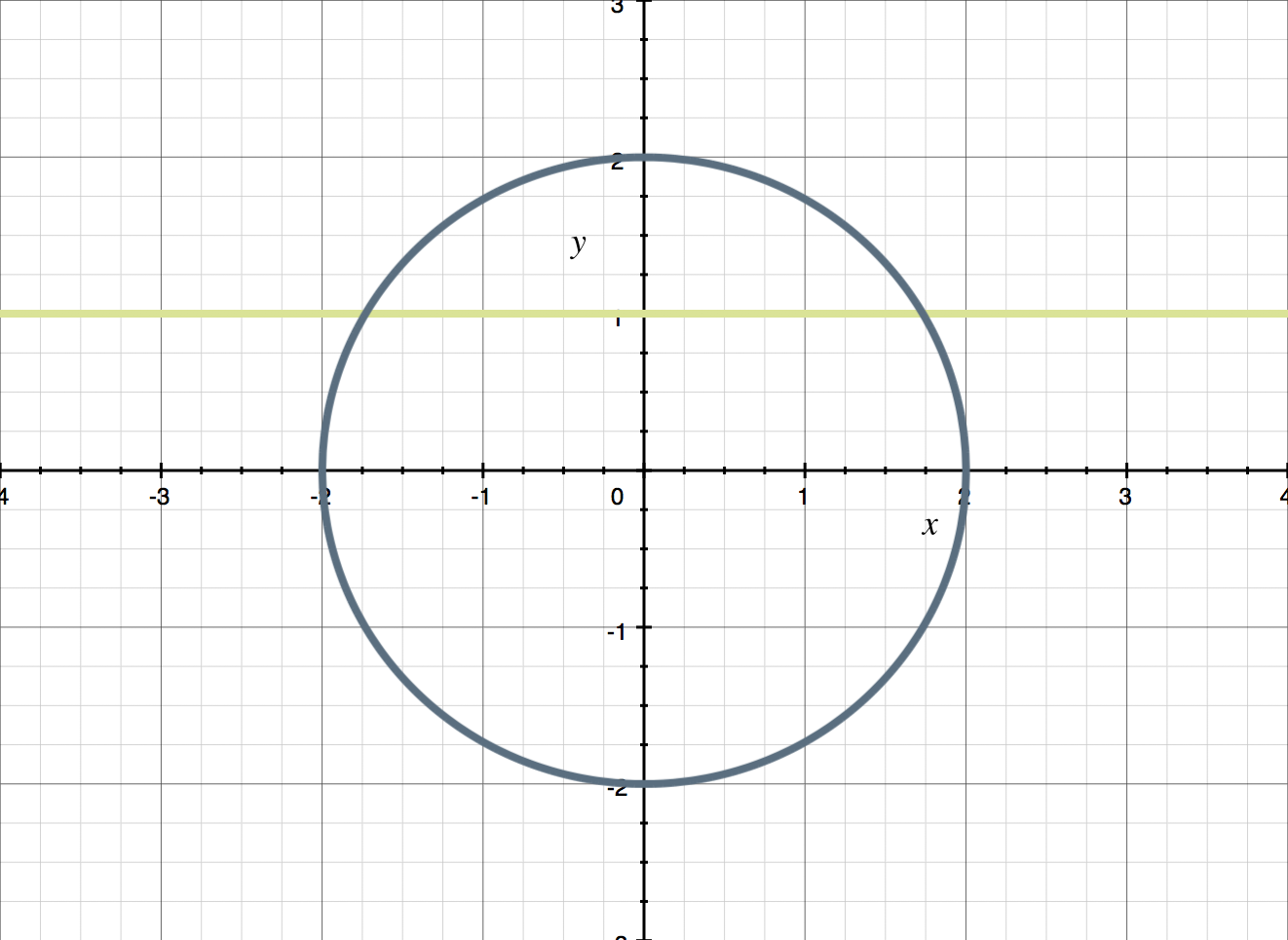
This graph doesn't pass the Horizontal Line Test because any horizontal line between ???y=-2??? and ???y=2??? would intersect it more than once.
All non-horizontal linear functions are one-to-one because a horizontal line drawn anywhere will only pass through once. A look at this next graph tells us that there’s no horizontal line that intersects the graph at more than one point, so the relation is a function.
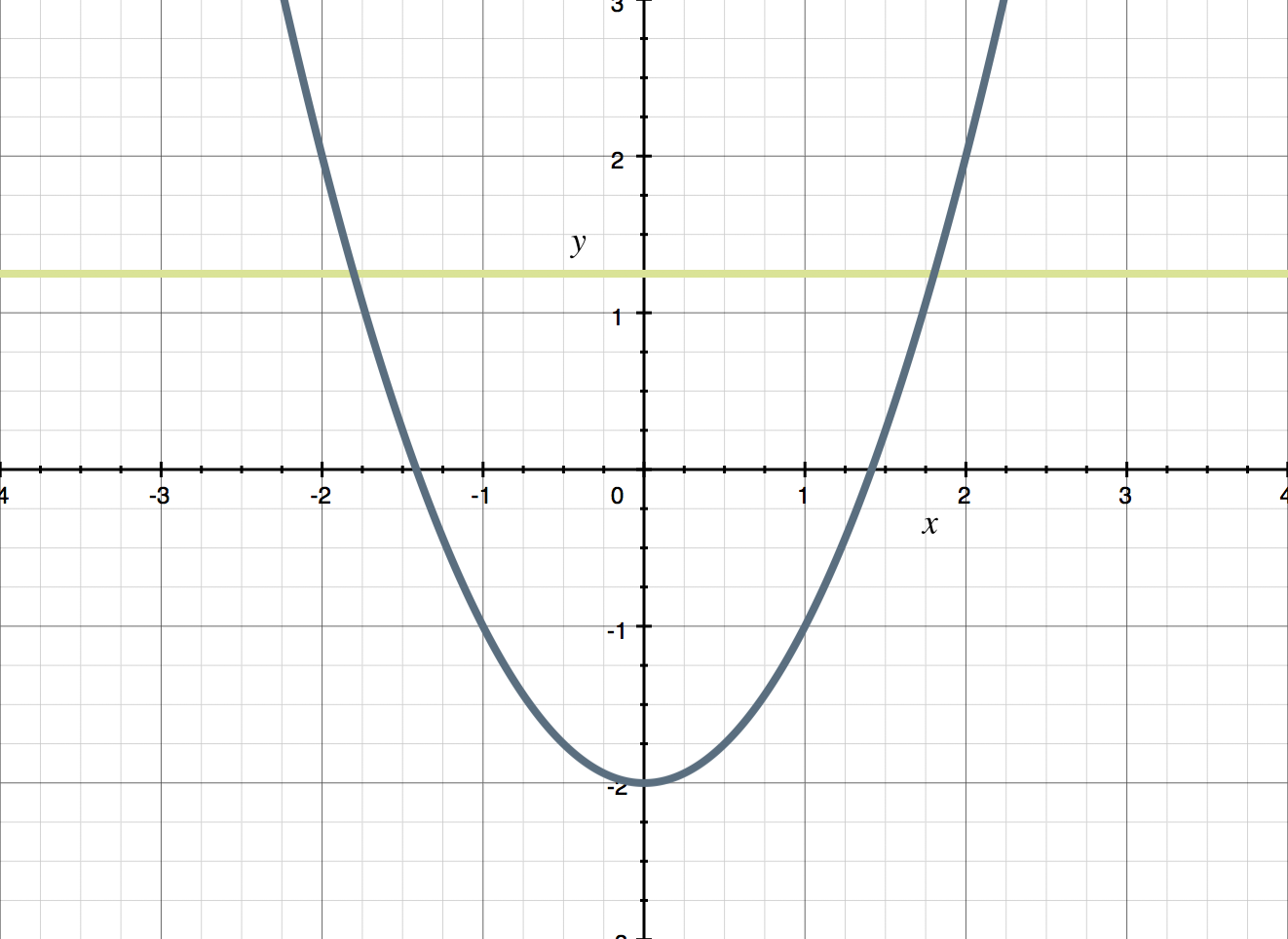
On the other hand, quadratic functions are never one-to-one. A look at the next graph shows us that it’s easy to find a horizontal line that intersects the graph at more than point, thereby proving that the function is not one-to-one.
This is one reason it’s a good idea to have an idea of what function families look like. If you’re familiar with what a group of functions look like, then you can think about the graph in your head to decide if it’s a one-to-one function. For example, quadratics form a “u” shape so a horizontal line would pass through the graph twice. That means quadratic functions are never one-to-one.
One-to-one functions algebraically
Another method to check for a one-to-one function is to think that ???f(a)=f(b)??? implies ???a=b??? in a one-to-one function.
Say we want to know if ???f(x)=\sqrt{x-2}??? is one-to-one without drawing or visualizing the graph.
Then we think if ???f(a)=f(b)??? then ???a=b??? and the function is one-to-one. We know that ???f(a)=\sqrt{a-2}??? and ???f(b)=\sqrt{b-2}???, so we could say
???f(a)=f(b)???
???\sqrt{a-2}=\sqrt{b-2}???
???\left(\sqrt{a-2}\right)^2=\left(\sqrt{b-2}\right)^2???
???a-2=b-2???
???a=b???
So ???f(x)??? is a one-to-one function.
How to use the Horizontal Line Test to determine whether or not a function is one-to-one
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Showing that the function is 1-to-1
Example
Show that the function is one-to-one by showing ???f(a)=f(b)??? leads to ???a=b???.
???f(x)=\frac{x-3}{x+4}???
We’ll start by replacing ???x??? with ???a???, and then setting that equal to whatever we get when we replace ???x??? with ???b???.
???\frac{a-3}{a+4}=\frac{b-3}{b+4}???
???(a-3)(b+4)=(b-3)(a+4)???
???ab+4a-3b-12=ab+4b-3a-12???
???4a+3a=4b+3b???
???7a=7b???
???a=b???
This means ???f(x)??? is a one-to-one function.
Let’s try another example.
On the other hand, quadratic functions are never one-to-one.
Example
Show that ???g(x)??? is not one-to-one by showing that ???f(a)=f(b)??? does not imply that ???a=b???.
???g(x)=x^2???
All we need is one case to show that ???f(a)=f(b)??? does not imply that ???a=b???. That means we can choose one example where ???f(a)=f(b)??? but ???a \neq b???. Consider the case when ???a=2??? and ???b=-2???, then ???a \neq b??? but
???f(-2)=(-2)^2=4???
and
???f(2)=(2)^2=4???
Therefore, ???f(2)=f(-2)??? but ???2 \neq -2???. Since we’ve found one case, the function is not one-to-one.