How to find and graph parallel and perpendicular lines
How to define parallel and perpendicular lines
In this lesson we’ll learn about the qualities that make up parallel and perpendicular lines and how to identify them on a graph or in an equation.
Remember, opposites are numbers with different signs, as a variable they can be expressed as ???m??? and ???-m??? (although this doesn’t mean that ???m??? is the positive number and ???-m??? is the negative number).
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Here are a few more examples of opposite pairs:
???4, \ -4???
???0.15 \ -0.15???
???\frac{3}{4}, \ -\frac{3}{4}???
Reciprocals are fractions that, when multiplied together give you ???1???. Usually we say they are “flipped” numbers. Here are some examples of reciprocals.
???\frac{1}{2}, \ 2???
???\frac{3}{5}, \ \frac{5}{3}???
???-\frac{2}{7}, \ -\frac{7}{2}???
The formula for a line in slope-intercept form is ???y=mx+b???, where ???m??? is the slope of the line and ???b??? is the ???y???-intercept.
Parallel lines
For two lines to be parallel, their slopes must be equal but the ???y???-intercepts must be different (otherwise they are the same line).
Algebraically, in slope-intercept form they would look like
???\begin{cases}y=mx+ b_{1} \\y=mx+b_{2}\end{cases}???
where ???b_{1} \neq b_{2}???.
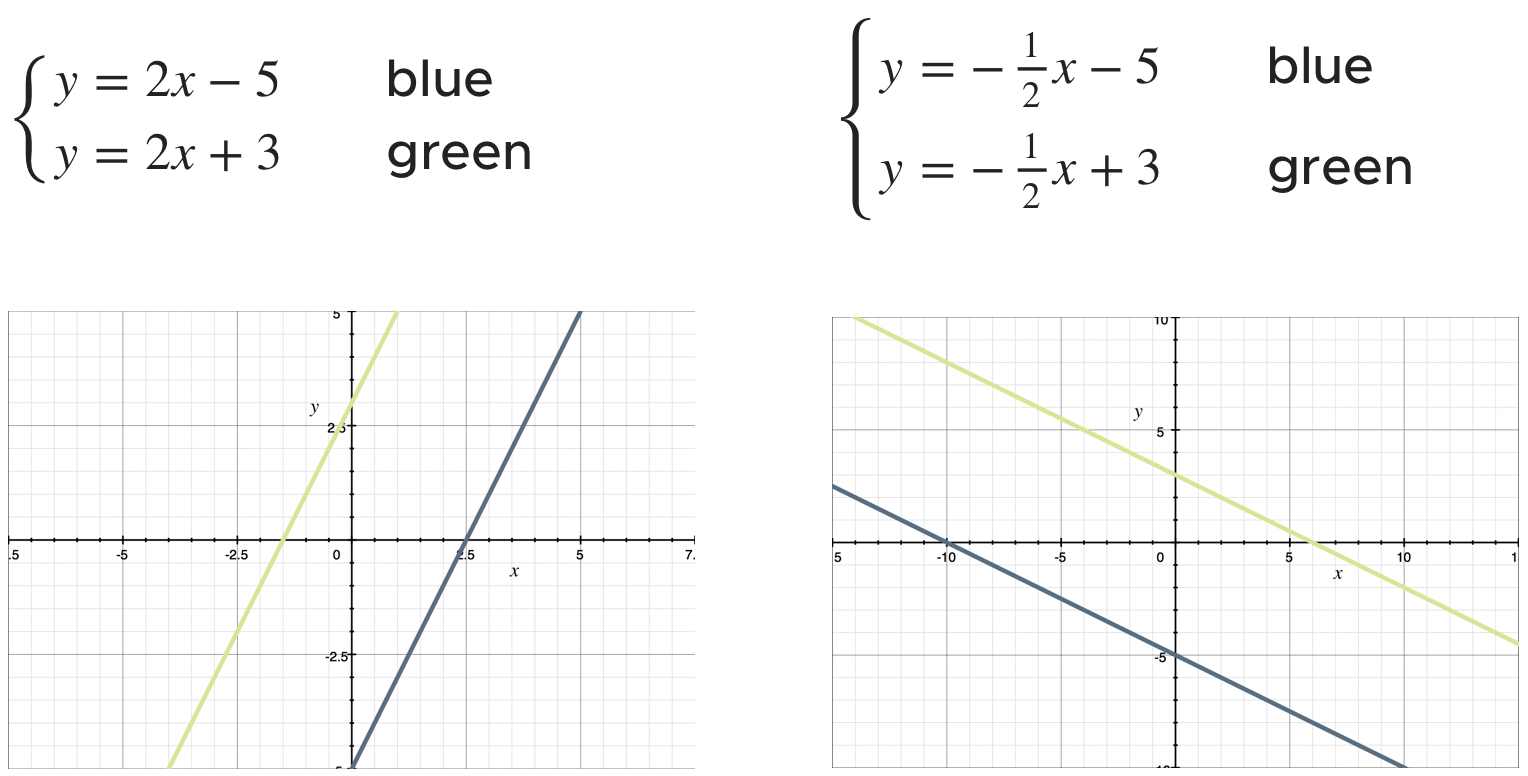
Here’s an example of what parallel lines could be written as in slope-intercept form.
???\begin{cases}y=2x-5 \\y=2x+3\end{cases}???
???\begin{cases}y=-\frac{1}{2}x-5 \\y=-\frac{1}{2}x+3\end{cases}???
These are both examples of parallel line pairs.
Parallel lines go on forever in the same direction and never cross one another. Here are the two examples of parallel line pairs when they are graphed.
Perpendicular lines
Perpendicular lines have opposite reciprocal slopes, so their ???y???-intercepts can be the same.
Algebraically, in slope-intercept form they would look like
???\begin{cases}y=mx+ b_{1} \\y=-\frac{1}{m}x+b_{2}\end{cases}???
where ???b_{1}??? and ???b_{2}??? could be the same.
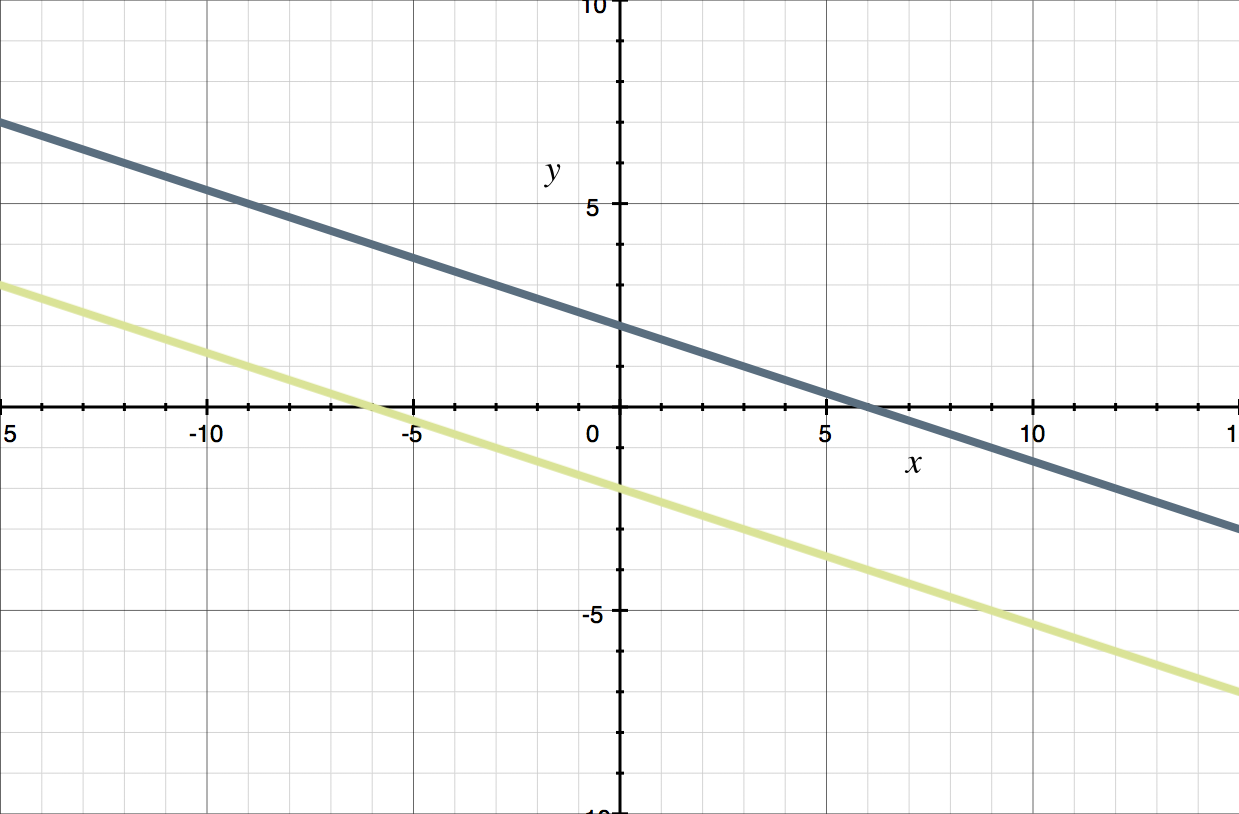
Here are two examples of perpendicular line pairs:
???\begin{cases}y=2x-3 \\y=-\frac{1}{2}x-3\end{cases}???
???\begin{cases}y=-5x+2 \\y=\frac{1}{5}x-4\end{cases}???
When perpendicular lines are graphed they cross each other and form four ???90??? degree angles. Be aware that checking this on your calculator might not always help because the graphing window settings can disguise right angles.
Here are the examples when they are graphed:
Let’s go ahead and look at a few of the types of questions you could be asked about when it comes to parallel and perpendicular lines.
Graphing pairs of parallel and perpendicular lines
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Finding pairs of parallel and perpendicular lines
Example
Write the equation of the line parallel to ???5x+2y=10??? with a ???y???-intercept of ???4???.
For two lines to be parallel, their slopes must be equal.
Remember that the equation of a line in slope-intercept form is given by
???y=mx+b???
where ???m??? is the slope of the line. We can rewrite the given equation as
???5x+2y=10???
???5x-5x+2y=-5x+10???
???2y=-5x+10???
???\frac{1}{2}\cdot 2y=\frac{1}{2}\cdot -5x+\frac{1}{2}\cdot 10???
???y=-\frac{5}{2}x+5???
The slope of the line is ???-5/2???.
We want to write an equation of a line with a slope of ???-5/2??? and a ???y???-intercept of ???4???. So ???m=-5/2??? and ???b=4???. Therefore, the equation is
???y=-\frac{5}{2}x+4???
Let’s look at another example.
For two lines to be parallel, their slopes must be equal but the Y-intercepts must be different (otherwise they are the same line).
Example
Graph the line parallel to the one in the graph with a ???y???-intercept of ???-2???.
Parallel lines go on forever in the same direction and have the same slope. We want to draw a line that never crosses this one but that goes through the ???y???-intercept of ???(0,-2)???.
Start by graphing the ???y???-intercept of ???-2???. Find the rise over run (the slope) of the original line from its ???y???-intercept, then follow the rise over run pattern on the new ???y???-intercept and draw a point. Connect the points and draw the parallel line.
The new line has an equation of
???y=-\frac{1}{3}x-2???
Let’s look at an example of a perpendicular line instead.
Example
Write the equation of the line passing through ???(-2,5)??? and perpendicular to
???y=-\frac{4}{7}x-2???
Remember, perpendicular lines have opposite reciprocal slopes. In other words, the slope of the new line needs to be the negative reciprocal of ???-4/7???, which means the slope of the new line is
???\frac{7}{4}???
The equation of a line in slope-intercept form is ???y=mx+b???. For our new line we know the slope and a point. The slope is ???m=7/4??? and the point is ???(-2,5)???.
We can plug the slope and point into the formula and solve for the ???y???-intercept ???b??? of the new line.
???5=\frac{7}{4}(-2)+b???
???5=-\frac{7}{2}+b???
???5+\frac{7}{2}=-\frac{7}{2}+\frac{7}{2}+b???
???\frac{17}{2}=b???
Now plug the slope and ???y???-intercept into the equation. The perpendicular line is
???y=\frac{7}{4}x+\frac{17}{2}???