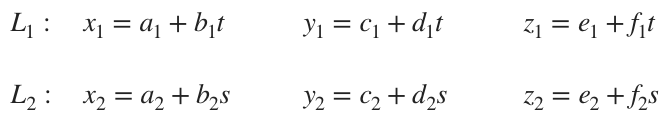Testing for parallel, intersecting, skew, and perpendicular lines

Two lines can be parallel, intersecting, or skew

To determine whether two lines are parallel, intersecting, skew or perpendicular, we will need to perform a number of tests on the two lines.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Given two lines,

then the lines are

parallel if the ratio equality is true.

$\frac{b_1}{b_2}=\frac{d_1}{d_2}=\frac{f_1}{f_2}$

intersecting if the lines are not parallel or if you can solve them as a system of simultaneous equations.

perpendicular if the lines are intersecting and their dot product is $0$.

$L_1\cdot L_2=0$

skew if the lines are not parallel and not intersecting.

How to determine if two lines are parallel, intersecting (or perpendicular specifically), or skew

---

Take the course

Want to learn more about Calculus 3? I have a step-by-step course for that. :)

---

Test for perpendicular first, then intersecting (then perpendicular if intersecting), and then skew

Example

Say whether the lines are parallel, intersecting, perpendicular or skew.

We’ll start by testing the lines to see if they’re parallel by pulling out the coefficients

$\frac{b_1}{b_2}=\frac{d_1}{d_2}=\frac{f_1}{f_2}$

$\frac53=\frac24=\frac{1}{-2}$

$\frac53=\frac12=\frac{1}{-2}$

Since $5/3\neq1/2\neq-1/2$, we know the lines are not parallel.

Because they’re not parallel, we’ll test to see whether or not they’re intersecting. We’ll set the equations for $x$, $y$, and $z$ from each line equal to each other. If we can find a solution set for the parameter values $s$ and $t$, and this solution set satisfies all three equations, then we’ve proven that the lines are intersecting.

Setting $x_1=x_2$, we get

$x_1=x_2$

$1+5t=2+3s$

$5t=1+3s$

[1] $t=\frac15+\frac35s$

Setting $y_1=y_2$, we get

$y_1=y_2$

[2] $-3+2t=3+4s$

Plugging [1] into [2] gives

$-3+2\left(\frac15+\frac35s\right)=3+4s$

$-3+\frac25+\frac65s=3+4s$

$-6+\frac25=4s-\frac65s$

$-\frac{28}{5}=\frac{14}{5}s$

$s=-\frac{28}{14}$

[3] $s=-2$

Plugging [3] into [1] gives

$t=\frac15+\frac35(-2)$

$t=\frac15-\frac65$

[4] $t=-1$

Setting $z_1=z_2$, we get

$z_1=z_2$

[5] $1+t=3-2s$

Plugging [3] and [4] into [5] gives

$1+t=3-2s$

$1+(-1)=3-2(-2)$

$0=7$

Since $0\neq7$, the lines are not intersecting.

Because $L_1$ and $L_2$ are not parallel and not intersecting, by definition they must be skew.

---

Two lines are intersecting if the lines are not parallel or if you can solve them as a system of simultaneous equations.

In the previous example, we didn’t test for perpendicularity because only intersecting lines can be perpendicular, and we found that the lines were not intersecting. If we had found that $L_1$ and $L_2$ were in fact perpendicular, we would have needed to test for perpendicularity by taking the dot product, like this:

$L_1\cdot L_2=(1+5t)(2+3s)+(-3+2t)(3+4s)+(1+t)(3-2s)$

$L_1\cdot L_2=2+3s+10t+15st-9-12s+6t+8st+3-2s+3t-2st$

$L_1\cdot L_2=21st-11s+19t-4$

$0\neq21st-11s+19t-4$

Since the dot product isn’t $0$, we’ve proven that the lines are not perpendicular.

---

Get access to the complete Calculus 3 course

---