Lines, parallel, perpendicular, or neither

Definitions of parallel and perpendicular lines

In this lesson we’ll look at how to use the slopes of two lines in the Cartesian plane (the $xy$ -plane) to see if the lines are perpendicular, parallel, or neither.

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

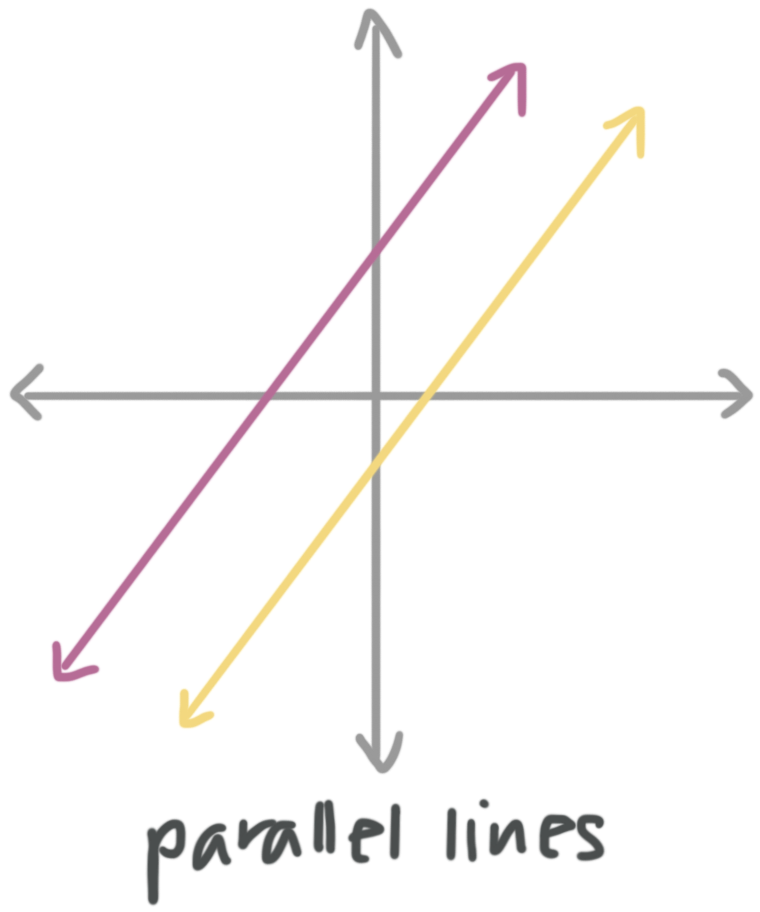
Parallel lines

Parallel lines are lines with equal slopes. Parallel lines will never intersect each other, because they’ll always be the same distance apart.

Perpendicular lines

Perpendicular lines have slopes that are negative reciprocals of each other, and they intersect to form $90^\circ$ angles.

How to determine whether two lines are perpendicular, parallel, or neither

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

Learn More

Determining which lines are parallel, and which ones are perpendicular

Example

Each pair of points in the table below are points that lie on the given line. Which lines are parallel to each other and which lines are perpendicular?

Use the slope formula for each line.

Slope of line $AB$ : $m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{11-1}{-3-3}=\frac{10}{-6}=-\frac53$

Slope of line $CD$ : $m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{5-2}{5-3}=\frac35$

Slope of line $EF$ : $m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{-2-(-5)}{0-(-5)}=\frac{-2+5}{0+5}=\frac35$

Lines $CD$ and $EF$ have the same slope, $3/5$ , so these two lines are parallel. Lines $AB$ and $CD$ have opposite reciprocal slopes so the lines are perpendicular. Lines $EF$ and $AB$ are also perpendicular for the same reason.

Let’s see how we can find the slope of a parallel line.

Lines parallel perpendicular or neither for Geometry.jpg — **Perpendicular lines** have slopes that are negative reciprocals of each other.

Example

What is the slope of a line parallel to $CD$ , if $CD$ passes through the points, $(4,5)$ and $(-2,8)$ ?

Parallel lines have the same slope, so first we need to find the slope of $CD$ . Use the slope formula.

$m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{8-5}{-2-4}=\frac{3}{-6}=-\frac{1}{2}$

Any line parallel to $CD$ will have a slope of $-1/2$ .

Now let’s look at how to find a perpendicular slope.

Example

What is the slope of a line perpendicular to $WX$ , if $WX$ passes through the points $(-3,5)$ and $(2,-6)$ ?

Perpendicular lines have opposite reciprocal slopes, so first we need to find the slope of $WX$ . Use the slope formula.

$m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{-6-5}{2-(-3)}=\frac{-11}{5}=-\frac{11}{5}$

Now we find the opposite reciprocal by flipping the fraction and multiplying by $-1$ to get $5/11$ . The slope of a line perpendicular to $WX$ is $5/11$ .