Pivot entries and row-echelon forms

Pivot entries are the starting point for putting matrices into reduced row-echelon form

Now that we know how to use row operations to manipulate matrices, we can use them to simplify a matrix in order to solve the system of linear equations the matrix represents.

Our goal will be to use these row operations to change the matrix into either row-echelon form, or reduced row-echelon form.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Let’s start by defining pivot entries, since they’re part of the definitions of row-echelon and reduced row echelon forms.

Pivot entries

Before we can understand row-echelon and reduced row-echelon forms, we need to be able to identify pivot entries in a matrix.

A pivot entry, (or leading entry, or pivot), is the first non-zero entry in each row. Any column that houses a pivot is called a pivot column. So in the matrix

the pivots are $4$ , $2$ , and $-3$ . And all three of the columns on the left side are pivot columns, since they each house a pivot entry.

Row-echelon forms

A matrix is in row-echelon form (ref) if

All the pivot entries are equal to $1$ .
Any row(s) that consist of only $0$ s are at the bottom of the matrix.
The pivot in each row sits in a column to the right of the column that houses the pivot in the row above it. In other words, the pivot entries sit in a staircase pattern, where they stair-step down from the upper left corner to the lower right corner of the matrix.

Row-echelon form might look like this:

In this matrix, the first non-zero entry in each row is a $1$ , the row consisting of only $0$ s is at the bottom, and the pivots follow a staircase pattern that moves down and to the right, so it’s in row-echelon form.

If a matrix is in row-echelon form (the matrix meets the three requirements above for row-echelon form), and if, in each pivot column, the pivot entry is the only non-zero entry, then the matrix is in reduced row-echelon form (rref). Reduced row-echelon form could look like this:

In this matrix, the first non-zero entry in each row is a $1$ , there are no rows consisting of only $0$ s, so we don’t need to worry about that requirement, the pivots follows a staircase pattern that moves down and to the right, and all three pivot columns include only the pivot entry, and otherwise only $0$ entries. The second column includes a non-zero entry, but it’s not a pivot column, so that’s okay, and this matrix is in reduced row-echelon form.

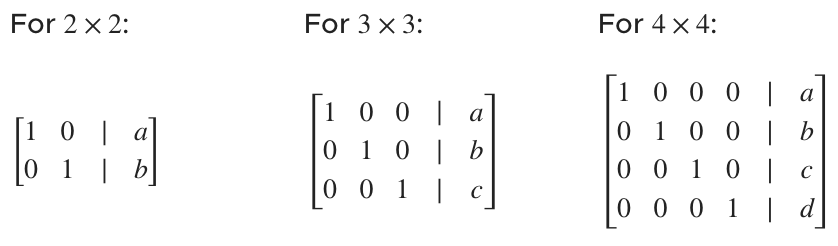
This is what reduced row-echelon form often looks like for $2\times2$ , $3\times3$ , and $4\times4$ augmented matrices:

If you do find a row of zeros in a matrix, either in row-echelon form or reduced row-echelon form, it tells you that the zero row was a combination of some of the other rows. It could be a multiple of another row, the sum or difference of other rows, or some other similar kind of combination.

How to rewrite matrices in both row-echelon (ref) and reduced row-echelon (rref) form

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

Learn More

Using row operations to put a matrix into reduced row-echelon form

Sometimes it’s fairly simple to put a matrix into row-echelon or reduced row-echelon form.

Example

Use row operations to put the matrix into reduced row-echelon form.

Notice that we can multiply $R_2$ by $1/5$ (or equivalently, divide $R_2$ by $5$ ).

Now we need to put the pivot entries into a staircase pattern. Switch the first and second rows, $R_1\leftrightarrow R_2$ .

Switch the third and fourth rows, $R_3\leftrightarrow R_4$ .

Now all the pivot entries are $1$ , the zeroed-out row is at the bottom, the pivot entries follow a staircase pattern, and all the pivot columns include only the pivot entry, and otherwise all $0$ entries. So the matrix is in reduced row-echelon form.

Let’s talk for a second about why we would want to put a matrix into rref. Remember that a rref matrix

is still representing a system of linear equations. So if we’ve put the matrix into reduced row-echelon form and then we pull back out the linear equations represented by the matrix, we get

$1x+0y+0z=a$

$0x+1y+0z=b$

$0x+0y+1z=c$

or just

$x=a$

$y=b$

$z=c$

In other words, from reduced row-echelon form, we automatically have the solution to the system! So what we’re saying is that, if we put the matrix into its reduced row-echelon form, then we can pull out the value of each variable directly from the matrix. You can almost think about reduced row-echelon form as the simplest, most “cleaned up” version of a matrix.