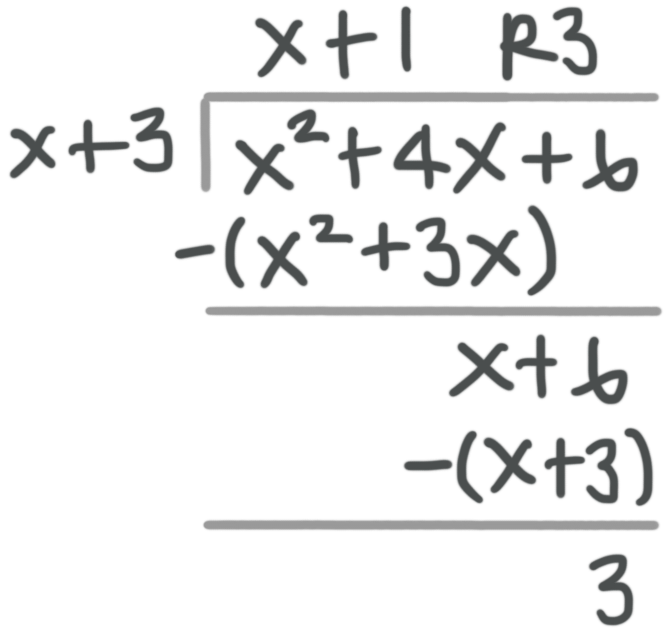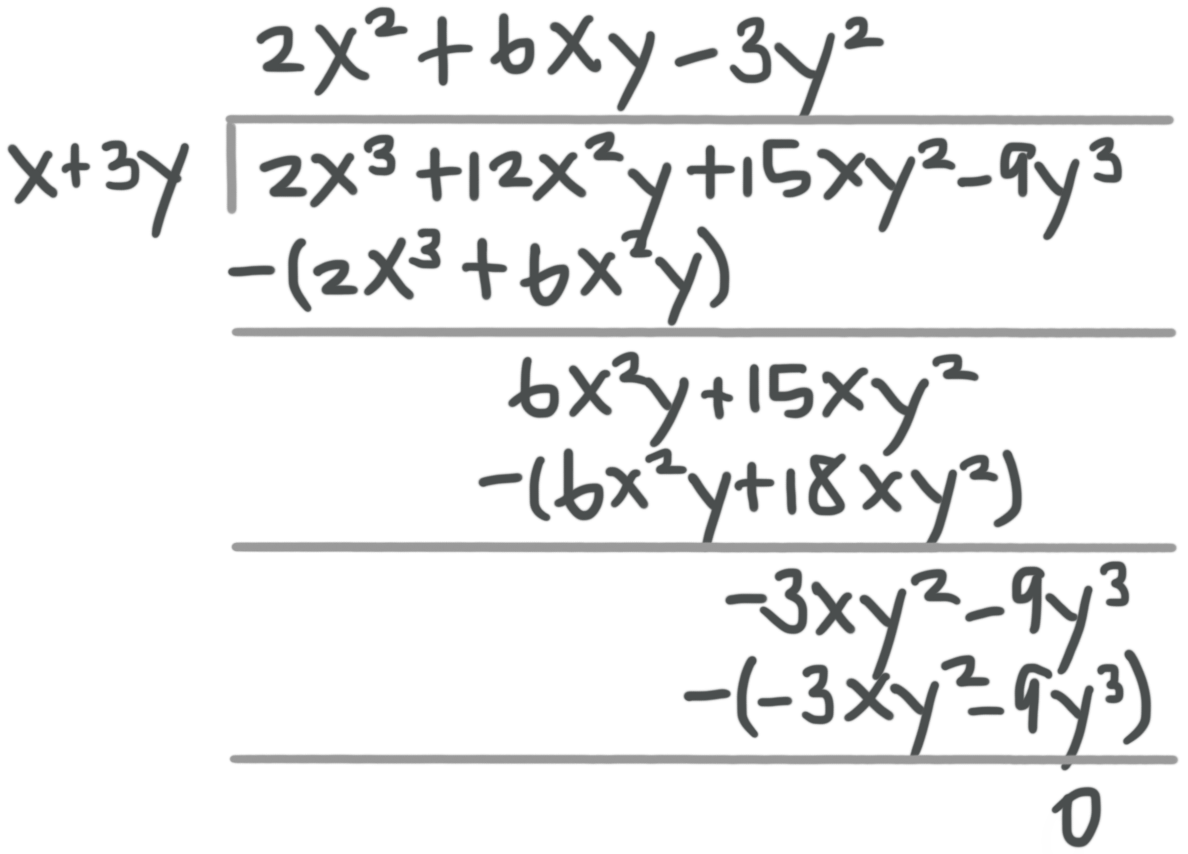How to do polynomial long division with multivariable polynomials

Dividing multivariable polynomials blog post.jpeg

Using polynomial long division with multiple variables

Dividing multivariable polynomials is very similar to dividing single-variable polynomials. We’ll still use long division, but now we’ll have more than one variable.

Let’s review long division by dividing $146$ by $13$ .

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

We start by thinking, “How many times does $13$ go into $14$ ?” It’s $1$ time, so we write a $1$ above the long division sign and line it up with the $4$ .

Then we multiply $13$ by $1$ and get $13$ , which means we subtract $13$ from $14$ and get $1$ . Bring down the $6$ .

How many times does $13$ go into $16$ ? $1$ time, so we write another $1$ above long division sign, this time line up with the $6$ .

$13\times1=13$ , which means we subtract $13$ from $16$ and get $3$ . Since $13$ doesn’t go into $3$ , we have a remainder of $3$ .

Our answer to $146\div 13$ is $11)with a remainder of$ 3???, or

$11 \frac{3}{13}$

Now let’s look at the same problem using polynomial long division. This time we’ll divide $x^2+4x+6$ by $x+3$ .

The leading term in the dividend ( $x^2+4x+6$ ) is $x^2$ , and the leading term in the divisor ( $x+3$ ) is $x$ . So we start by thinking, “What do I need to multiply $x$ by to get $x^2$ ?” The answer is $x$ , so we write $x$ above the long division sign and line it up with the $x^2$ .

Then we multiply $x+3$ by $x$ and get $x^2+3x$ , which means we subtract $x^2+3x$ from $x^2+4x$ and get $x$ . Bring down the $+6$ .

What do we need to multiply $x$ by in order to get $x$ ? The answer is $1$ , so we write $+1$ next to the $x$ above the long division sign.

$(x+3)\cdot1=x+3$ , so subtract $x+3$ from $x+6$ and get $3$ .

Our answer is $x+1$ with a remainder of $3$ . When we do polynomial long division, we should write the remainder as a fraction, with the remainder in the numerator and the divisor in the denominator, so the answer can be written as

$x+1+\frac{3}{x+3}$

Remember to always have placeholders for any “missing” terms (terms that have a coefficient of $0$ ) in the dividend. For example, if the problem above hadn’t had an $x$ term, we would have needed to write $x^2+0x+6$ under the long division sign.