Projections of the curve onto the coordinate planes
What are the projections of a three-dimensional curve
Sometimes the easiest way to sketch a three-dimensional curve is to sketch its projections on the ???xy???-, ???xz???-, and ???yz???-coordinate planes.
Think about the projections of a curve as the shadows they cast against the coordinate planes.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
You can also think about them as the view of the curve from the coordinate planes. In other words, if you’re standing squarely parallel to the ???xy???-coordinate plane, what you see of the curve is the projection of the curve on the ???xy???-coordinate plane.
Once we have the projections of the curve on each of the coordinate planes, we can use them to draw the three-dimensional graph.
How to find the equation of each projection and then sketch the projections in two dimensions
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Projections of a vector function
Example
Sketch the projections of the curve and use them to sketch the three-dimensional curve.
???r(t)=\langle{t},t^2,t^2+1\rangle???
We’ll convert the vector function to three parametric equations.
???x=t???
???y=t^2???
???z=t^2+1???
To find the projection on the ???xy???-coordinate plane, we need to find an equation in terms of only ???x??? and ???y???, which we’ll do by plugging ???x=t??? into ???y=t^2???.
???y=t^2???
???y=x^2???
We’ll sketch this curve in the ???xy???-coordinate plane.
Think about the projections of a curve as the shadows they cast against the coordinate planes.
To find the projection on the ???xz???-coordinate plane, we need to find an equation in terms of only ???x??? and ???z???, which we’ll do by plugging ???x=t??? into ???z=t^2+1???.
???z=t^2+1???
???z=x^2+1???
We’ll sketch this curve in the ???xz???-coordinate plane.
To find the projection on the ???yz???-coordinate plane, we need to find an equation in terms of only ???y??? and ???z???, which we’ll do by plugging ???y=t^2??? into ???z=t^2+1???.
???z=t^2+1???
???z=y+1???
We’ll sketch this curve in the ???yz???-coordinate plane.
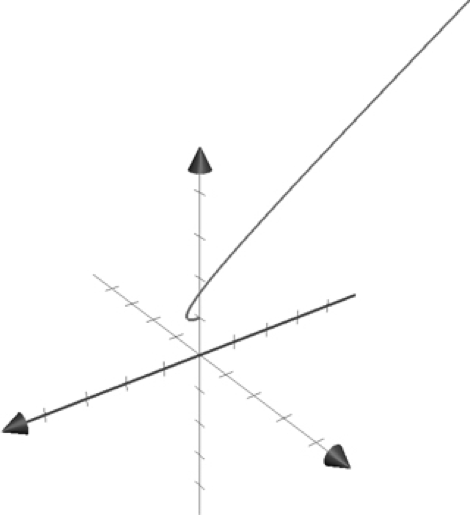
Our final step is to use the projections to sketch the three-dimensional curve. We need a starting point. To find it, we’ll set ???t=0??? in our parametric equations, and get
???x=t???
???x=0???
and
???y=t^2???
???y=0^2???
???y=0???
and
???z=t^2+1???
???z=0^2+1???
???z=1???
Putting these values together, we get the point ???(0,0,1)???. This means that our graph starts at ???(0,0,1)??? and travels upwards in a parabolic shape from the ???xy???- and ???xz???-planar perspective. The three-dimensional graph is