Understanding Rolle's Theorem
What does Rolle’s Theorem say?
Rolle’s Theorem is a specific instance of the Mean Value Theorem, in which the endpoints of the function at the edges of the interval are equal to one another.
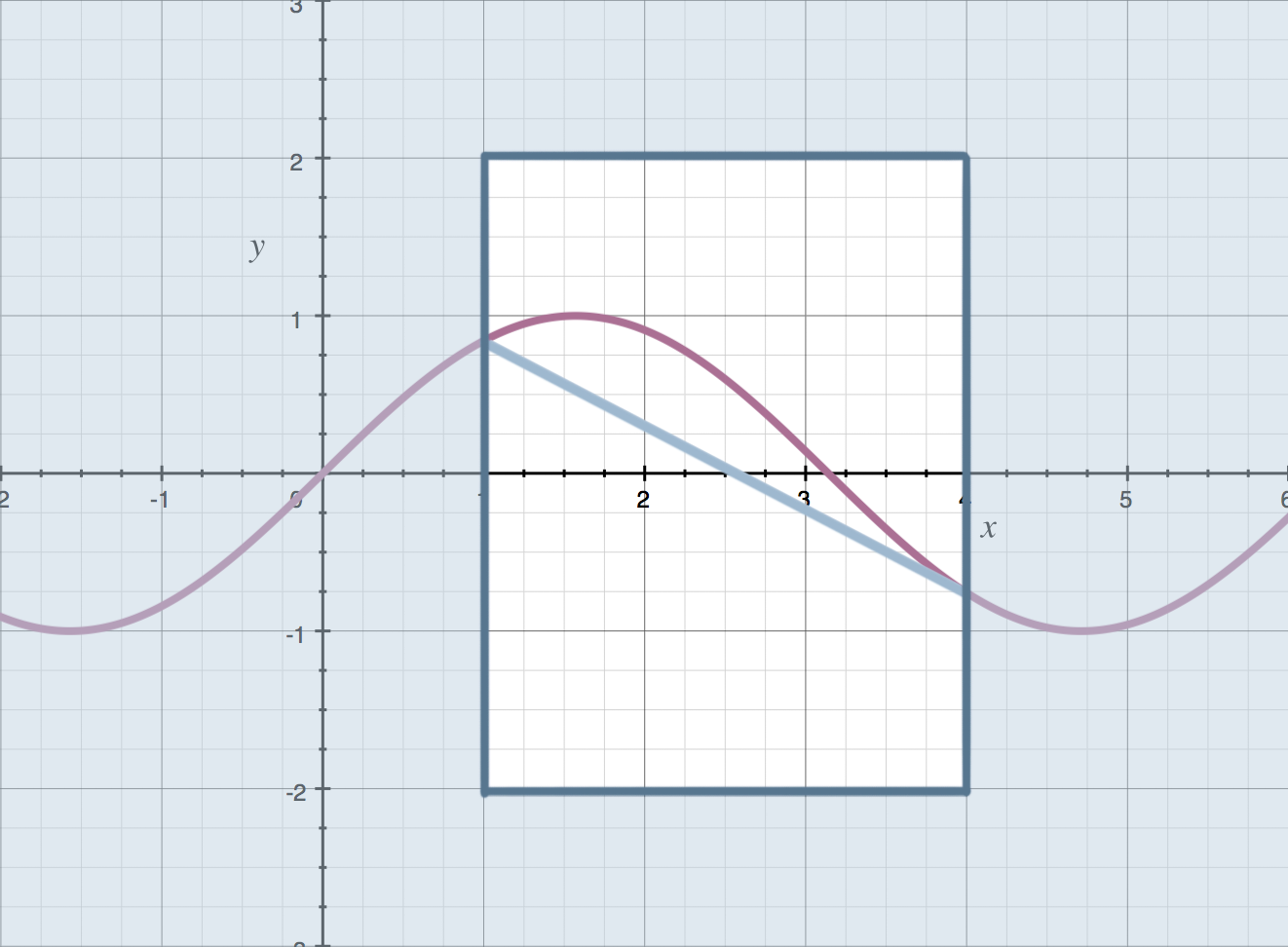
In the Mean Value Theorem lesson, we looked at a function in an interval, and the line that connected the endpoints was slanted.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
But to apply Rolle’s Theorem, the values of the function at the endpoints must be equal, which means the line that connects them will be perfectly horizontal.
Just like the Mean Value Theorem, Rolle’s Theorem tells us that, as long as the function is continuous (unbroken) and differentiable (smooth) inside the interval, then there must be a tangent line that’s parallel to the horizontal line that connects the endpoints.
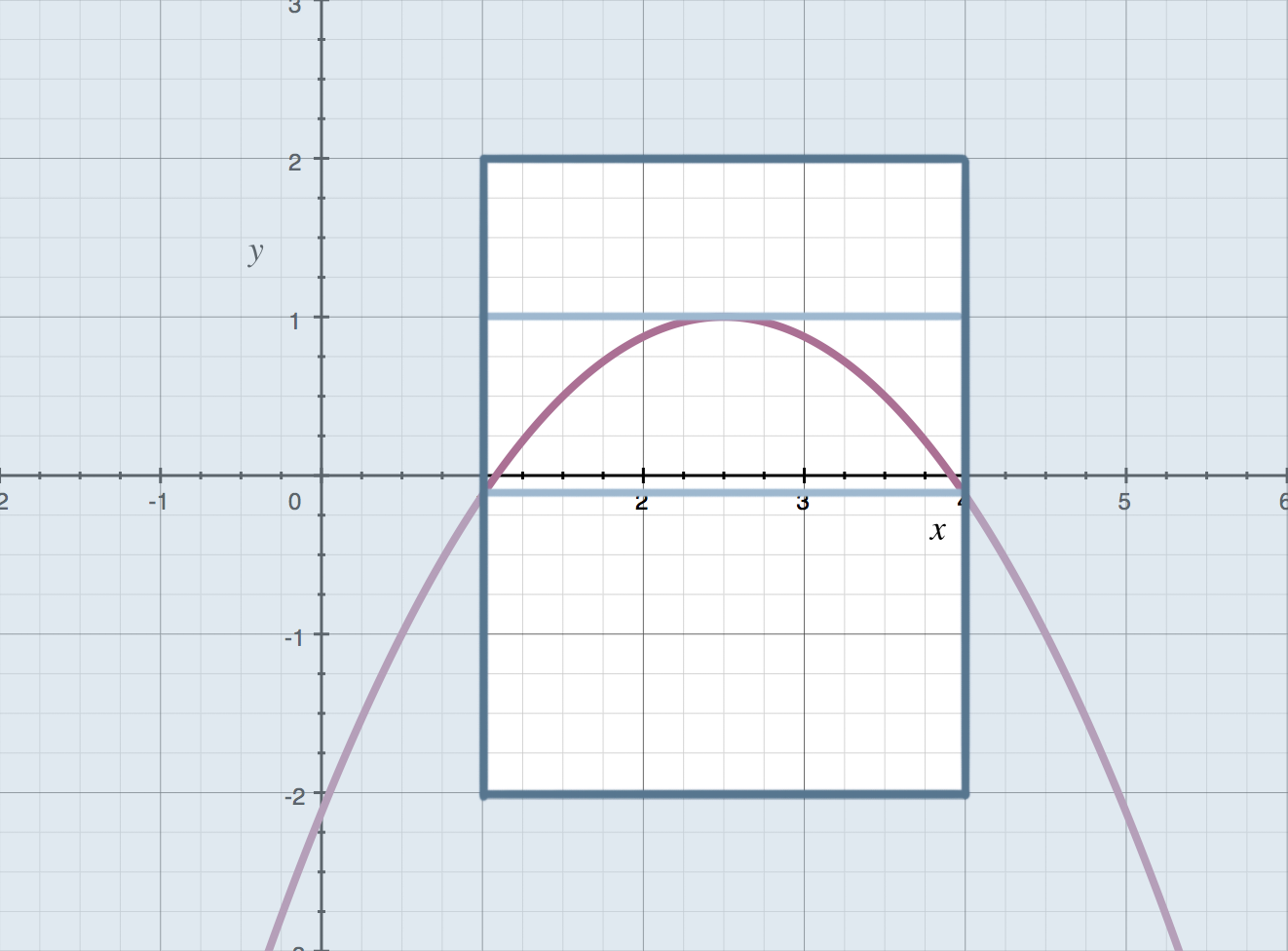
Here’s where that tangent line exists for this particular function we’ve been using:
Notice how it’s parallel to the line that connects the endpoints. This is what Rolle’s Theorem guarantees: a tangent line, somewhere inside the interval, that’s parallel to the line that connects the endpoints.
Because the line that connects the endpoints is horizontal, the tangent line will also be horizontal. Remember that horizontal tangent lines exist wherever the derivative is equal to ???0???, so Rolle’s Theorem can prove all of the following:
The existence of a horizontal tangent line in the interval
A point at which the derivative is ???0??? in the interval
The existence of a critical point in the interval
A point at which the function changes direction in the interval, either from increasing to decreasing, or from decreasing to increasing
The point at which that tangent line intersects the curve (the point of tangency) will exist at ???x=c???. We call the interval ???[a,b]???, so ???c??? will fall between ???a??? and ???b???, ???a<c<b???.
We can prove Rolle’s Theorem if we start from the Mean Value Theorem. The Mean Value Theorem says
???f'(c)=\frac{f(b)-f(a)}{b-a}???
But if the endpoints are equal, then ???f(a)=f(b)???, so we could make a substitution, and get
???f'(c)=\frac{f(b)-f(b)}{b-a}???
???f'(c)=\frac{0}{b-a}???
???f'(c)=0???
This result tells us that, by assuming the endpoints were equal, we found a value of ???0??? for the derivative at ???x=c??? in the interval, which is exactly what Rolle’s Theorem states.
How to use Rolle’s Theorem to prove the existence of roots in the interval
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Finding roots with Rolle’s Theorem
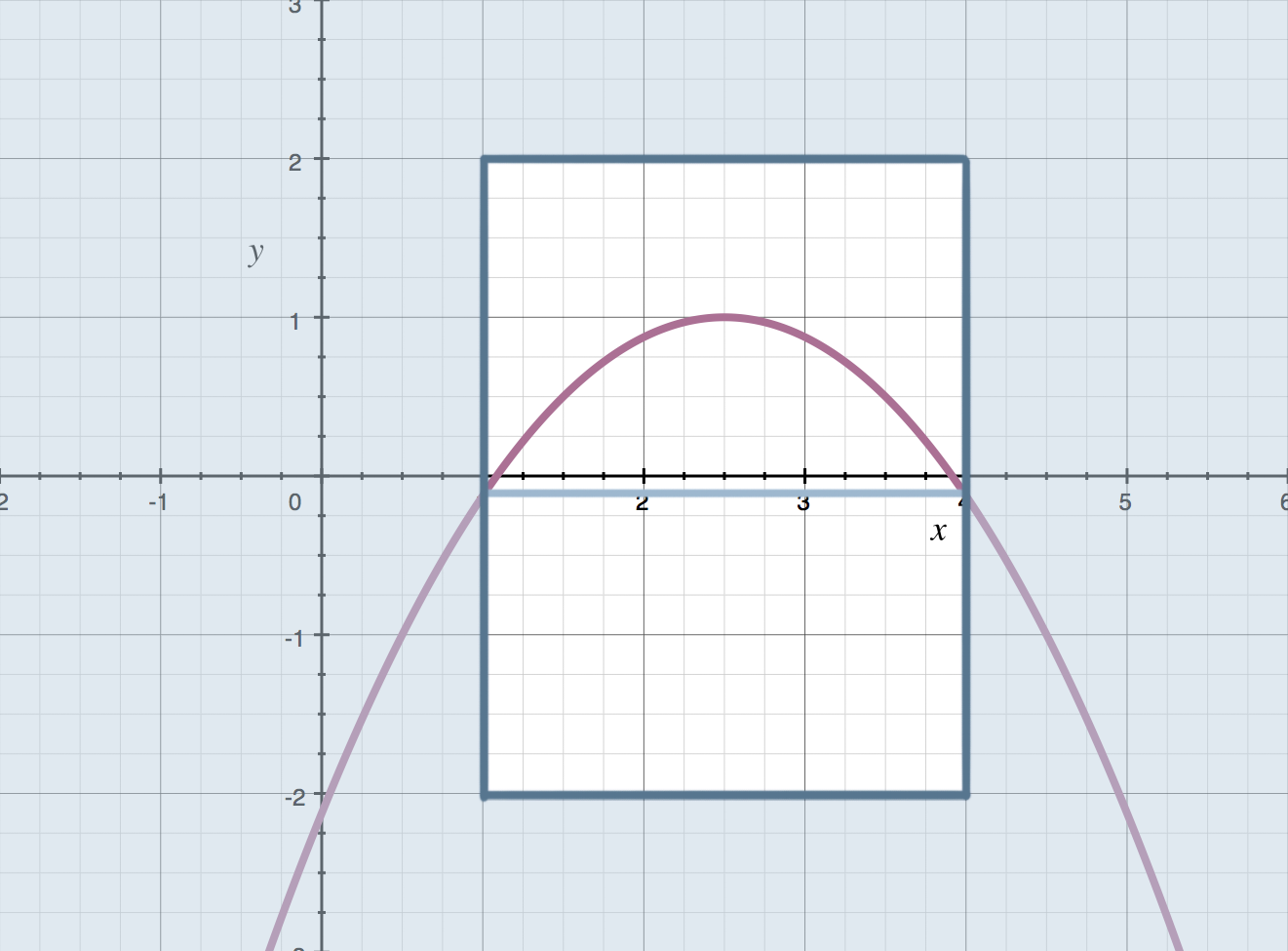
Use Rolle’s Theorem to show that the function has a critical point in the interval ???[0,2]???.
???f(x)=-\frac12x^4+2x^2???
A polynomial function like this one will be continuous and differentiable everywhere in its domain. Then all we need to do is check to make sure that the function’s value is equal at the endpoints of the interval, ???x=0??? and ???x=2???.
???f(0)=-\frac12(0)^4+2(0)^2???
???f(0)=0???
and
???f(2)=-\frac12(2)^4+2(2)^2???
???f(2)=-\frac12(16)+2(4)???
???f(2)=-8+8???
???f(2)=0???
A polynomial function like this one will be continuous and differentiable everywhere in its domain. Then all we need to do is check to make sure that the function’s value is equal at the endpoints of the interval.
The value of the function is ???0??? at both endpoints. It’s not necessary, but we could verify this visually if we wanted to double-check ourselves.
Because the endpoints of the interval are equal to one another, Rolle’s Theorem tells us that there must be a critical point somewhere in the interval.