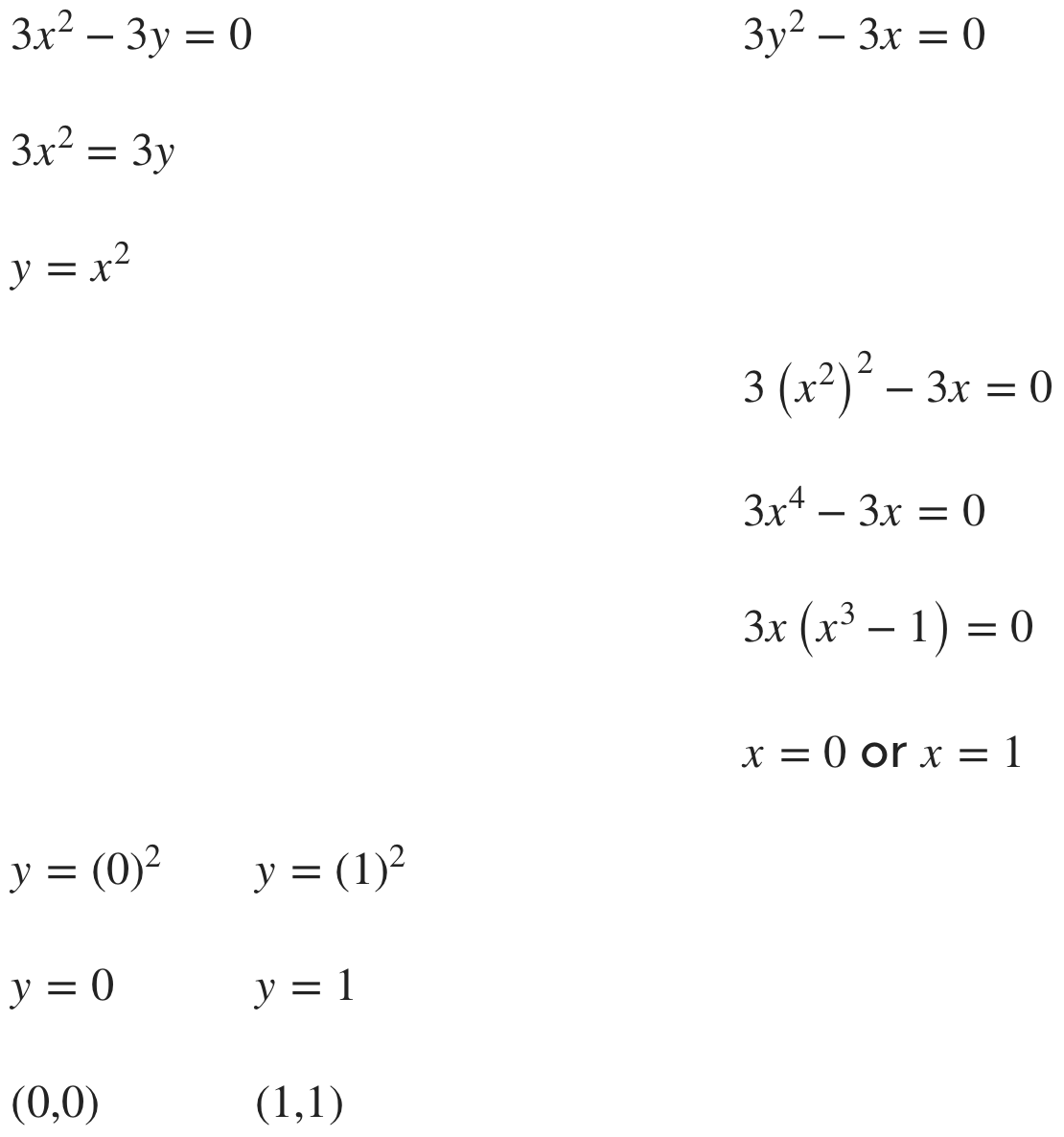Using the second derivative test to classify extrema of a multivariable function
What is the second derivative test for multivariable functions?
Just as we did with single variable functions, we can use the second derivative test with multivariable functions to classify any critical points that the function might have.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
To use the second derivative test, we’ll need to take partial derivatives of the function with respect to each variable. Once we have the partial derivatives, we’ll set them equal to ???0??? and use these as a system of simultaneous equations to solve for the coordinates of all possible critical points.
In order to classify the critical points we find using the second derivative test, we’ll need to find the second-order partial derivatives and plug them into the formula,
???D(x,y)=\frac{\partial^2{f}}{\partial{x^2}}\cdot\frac{\partial^2{f}}{\partial{y^2}}-\left(\frac{\partial^2{f}}{\partial{x}\partial{y}}\right)^2???
If ???D(x,y)<0???, then ???f??? has a saddle point at ???(x,y)???
If ???D(x,y)=0???, then the test is inconclusive
If ???D(x,y)>0??? and
???\frac{\partial^2{f}}{\partial{x^2}}(x,y)>0???, then ???f??? has a local minimum at ???(x,y)???
???\frac{\partial^2{f}}{\partial{x^2}}(x,y)<0???, then ???f??? has a local maximum at ???(x,y)???
How to use the second derivative test to classify the extrema of the multivariable function
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Finding and classifying multiple critical points for a multivariable function
Example
Find and classify the critical points of the function.
???f(x,y)=6+x^3+y^3-3xy???
We’ll start by finding the first-order partial derivatives.
???\frac{\partial{f}}{\partial{x}}=3x^2-3y???
and
???\frac{\partial{f}}{\partial{y}}=3y^2-3x???
Setting both of them equal to ???0??? and using these as a system of simultaneous equations to find critical points gives
Once we have the partial derivatives, we’ll set them equal to 0 and use these as a system of simultaneous equations to solve for the coordinates of all possible critical points.
To test these critical points, we’ll use the second derivative test by calculating the second-derivatives.
???\frac{\partial^2{f}}{\partial{x^2}}=6x???
???\frac{\partial^2{f}}{\partial{y^2}}=6y???
???\frac{\partial^2{f}}{\partial{x}\partial{y}}=-3???
Plugging these into the second derivative test formula, we get
???D(x,y)=\frac{\partial^2{f}}{\partial{x^2}}\cdot\frac{\partial^2{f}}{\partial{y^2}}-\left(\frac{\partial^2{f}}{\partial{x}\partial{y}}\right)^2???
???D(x,y)=(6x)(6y)-(-3)^2???
???D(x,y)=36xy-9???
Now we can use the equation for ???D(x,y)??? to test our critical points one at a time.
For ???(0,0)???:
???D(0,0)=36(0)(0)-9???
???D(0,0)=-9???
Since ???-9<0???, the function has a saddle point at ???(0,0)???.
For ???(1,1)???:
???D(1,1)=36(1)(1)-9???
???D(1,1)=27???
Since ???27>0???, we have to look at ???\partial^2{f}/\partial{x^2}??? to evaluate ???(1,1)??? further.
???\frac{\partial^2{f}}{\partial{x^2}}=6x???
???\frac{\partial^2{f}}{\partial{x^2}}(1,1)=6(1)???
???\frac{\partial^2{f}}{\partial{x^2}}(1,1)=6???
Since ???6>0???, the function has a local minimum at ???(1,1)???.
To summarize our findings, we can say that the function has
a saddle point at ???(0,0)???
a local minimum at ???(1,1)???