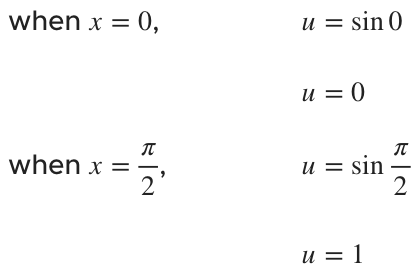U-substitution to solve definite integrals
U-substitution in definite integrals is a little different than substitution in indefinite integrals
U-substitution in definite integrals is just like substitution in indefinite integrals except that, since the variable is changed, the limits of integration must be changed as well.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
When using u-substitution in definite integrals, you either have to change the limits of integration, or back-substitute
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Evaluating a definite integral using u-substitution
Example
Use u-substitution to evaluate the integral.
???\int_0^{\frac{\pi}{2}}\frac{\cos{x}}{1+\sin^2{x}}\ dx???
Let
???u=\sin{x}???
???du=\cos{x}\ dx???
???dx=\frac{du}{\cos{x}}???
Since we’re dealing with a definite integral, we need to use the equation ???u=\sin{x}??? to find limits of integration in terms of ???u???, instead of ???x???.
U-substitution in definite integrals is just like substitution in indefinite integrals except that, since the variable is changed, the limits of integration must be changed as well.
Substituting back into the integral (including for our limits of integration), we get
???\int_0^1\frac{\cos{x}}{1+u^2}\cdot\frac{du}{\cos{x}}???
???\int_0^1\frac{1}{1+u^2}\ du???
Using this very common formula,
???\int\frac{1}{1+x^2}\ dx=\tan^{-1}{x}+C???
take the integral.
???\int_0^1\frac{1}{1+u^2}\ du=\tan^{-1}{u}\big|_0^1???
???\int_0^1\frac{1}{1+u^2}\ du=\tan^{-1}{1}-\tan^{-1}{0}???
???\int_0^1\frac{1}{1+u^2}\ du=\frac{\pi}{4}???