Tangential and normal components of the acceleration vector
What are the tangential and normal components of a vector?
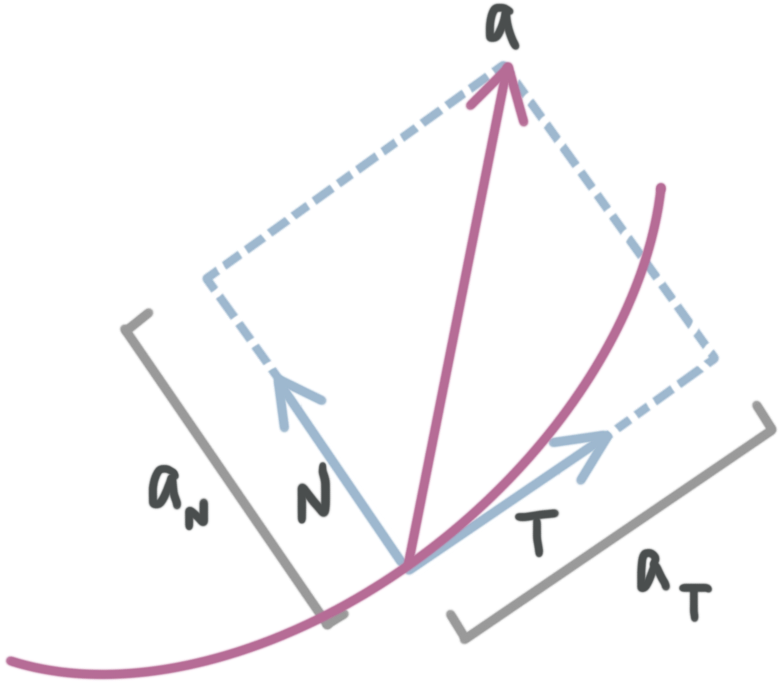
At any given point along a curve, we can find the acceleration vector ???a??? that represents acceleration at that point.
If we find the unit tangent vector ???T??? and the unit normal vector ???N??? at the same point, then the tangential component of acceleration ???a_T??? and the normal component of acceleration ???a_N??? are shown in the diagram below.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Tangential component of acceleration
???a_T=\frac{r'(t)\cdot{r''(t)}}{\left|r'(t)\right|}???
Normal component of acceleration
???a_N=\frac{\left|r'(t)\times{r''(t)}\right|}{\left|r'(t)\right|}???
In these formulas for the tangential and normal components,
???r(t)??? is the position vector, ???r(t)=r(t)_1\bold i+r(t)_2\bold j+r(t)_3\bold k???
???r'(t)??? is its first derivative, ???r'(t)=r'(t)_1\bold i+r'(t)_2\bold j+r'(t)_3\bold k???
???r''(t)??? is its second derivative, ???r''(t)=r''(t)_1\bold i+r''(t)_2\bold j+r''(t)_3\bold k???
???r'(t)\cdot{r''(t)}??? is the dot product of the first and second derivatives, ???r'(t)\cdot{r''(t)}=r'(t)_1r''(t)_1+r'(t)_2r''(t)_2+r'(t)_3r''(t)_3???
???\left|r'(t)\right|??? is the magnitude of the first derivative, ???\left|r'(t)\right|=\sqrt{\left[r'(t)_1\right]^2+\left[r'(t)_2\right]^2+\left[r'(t)_3\right]^2}???
???\left|r'(t)\times{r''(t)}\right|??? is the magnitude of the cross product of the first and second derivatives, where the cross product is ???r'(t)\times{r''(t)}=\begin{vmatrix}\bold i & \bold j & \bold k\\ r'(t)_1 & r'(t)_2 & r'(t)_3\\ r''(t)_1 & r''(t)_2 & r''(t)_3\end{vmatrix}???
We’ll start by finding each of the pieces in the list above, and then we’ll plug them into the formulas for the tangential and normal components of the acceleration vector.
How to find the tangential and normal components of an acceleration vector
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Finding the tangential component and normal component of a vector function
Example
Find the tangential and normal components of the acceleration vector.
???r(t)=2t^2\bold i+4t\bold j+3t^3\bold k???
We’ll start by finding ???r'(t)???, the derivative of the position function. To find the derivative, we’ll just replace the coefficients on ???\bold i???, ???\bold j??? and ???\bold k??? with their derivatives.
???r'(t)=4t\bold i+4\bold j+9t^2\bold k???
can also be written as ???r'(t)=\left\langle4t,4,9t^2\right\rangle???
We’ll repeat the process to find the second derivative.
???r''(t)=4\bold i+0\bold j+18t\bold k???
???r''(t)=4\bold i+18t\bold k???
can also be written as ???r''(t)=\left\langle4,0,18t\right\rangle???
Now we’ll find the dot product of the first and second derivatives.
???r'(t)\cdot{r''(t)}=(4t)(4)+(4)(0)+(9t^2)(18t)???
???r'(t)\cdot{r''(t)}=16t+0+162t^3???
???r'(t)\cdot{r''(t)}=16t+162t^3???
???r'(t)\cdot{r''(t)}=162t^3+16t???
Now we’ll find the magnitude of the first derivative.
???\left|r'(t)\right|=\sqrt{\left[r'(t)_1\right]^2+\left[r'(t)_2\right]^2+\left[r'(t)_3\right]^2}???
???\left|r'(t)\right|=\sqrt{\left(4t\right)^2+\left(4\right)^2+\left(9t^2\right)^2}???
???\left|r'(t)\right|=\sqrt{16t^2+16+81t^4}???
???\left|r'(t)\right|=\sqrt{81t^4+16t^2+16}???
If we find the unit tangent vector T and the unit normal vector N at the same point, then we can define the the tangential component of acceleration and the normal component of acceleration.
Finally, we’ll get the cross product of the first and second derivatives, then find its magnitude.
???r'(t)\times{r''(t)}=\begin{vmatrix}\bold i & \bold j & \bold k\\ r'(t)_1 & r'(t)_2 & r'(t)_3\\ r''(t)_1 & r''(t)_2 & r''(t)_3\end{vmatrix}???
???r'(t)\times{r''(t)}=\begin{vmatrix}\bold i & \bold j & \bold k\\ 4t & 4 & 9t^2\\ 4 & 0 & 18t\end{vmatrix}???
???r'(t)\times{r''(t)}=\begin{vmatrix}4 & 9t^2\\ 0 & 18t\end{vmatrix}\bold i-\begin{vmatrix}4t & 9t^2\\ 4 & 18t\end{vmatrix}\bold j+\begin{vmatrix}4t & 4\\ 4 & 0 \end{vmatrix}\bold k???
???r'(t)\times{r''(t)}=\left[(4)(18t)-(0)\left(9t^2\right)\right]\bold i-\left[(4t)(18t)-(4)\left(9t^2\right)\right]\bold j+\left[(4t)(0)-(4)(4)\right]\bold k???
???r'(t)\times{r''(t)}=\left(72t-0\right)\bold i-\left(72t^2-36t^2\right)\bold j+\left(0-16\right)\bold k???
???r'(t)\times{r''(t)}=72t\bold i-36t^2\bold j-16\bold k???
???r'(t)\times{r''(t)}=4\left(18t\bold i-9t^2\bold j-4\bold k\right)???
can also be written as ???r'(t)\times{r''(t)}=4\left\langle18t,-9t^2,-4\right\rangle???
Now we just need the magnitude of the cross product.
???\left|r'(t)\times{r''(t)}\right|=4\sqrt{(18t)^2+\left(-9t^2\right)^2+(-4)^2}???
???\left|r'(t)\times{r''(t)}\right|=4\sqrt{324t^2+81t^4+16}???
???\left|r'(t)\times{r''(t)}\right|=4\sqrt{81t^4+324t^2+16}???
We’ve finally found everything we need to solve for the tangential and normal components of acceleration. Plugging in what we know, we get
The tangential component of acceleration
???a_T=\frac{r'(t)\cdot{r''(t)}}{\left|r'(t)\right|}???
???a_T=\frac{162t^3+16t}{\sqrt{81t^4+16t^2+16}}???
The normal component of acceleration
???a_N=\frac{\left|r'(t)\times{r''(t)}\right|}{\left|r'(t)\right|}???
???a_N=\frac{4\sqrt{81t^4+324t^2+16}}{\sqrt{81t^4+16t^2+16}}???
???a_N=4\sqrt{\frac{81t^4+324t^2+16}{81t^4+16t^2+16}}???
These are the tangential and normal components of the acceleration vector.