How to identify functions, plus how to use the Vertical Line Test
A function relates x-inputs to y-outputs
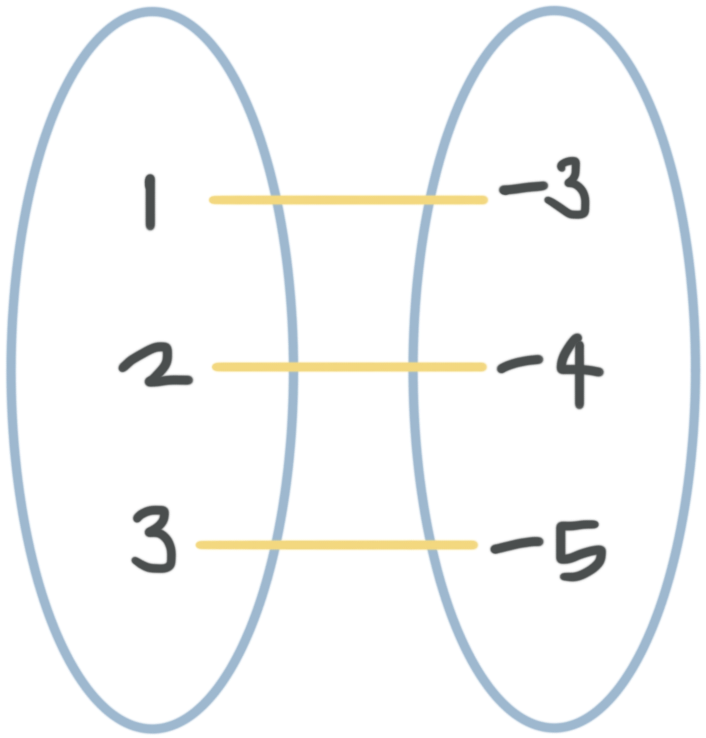
A function is a special kind of relation. Functions are special because each input is related to one and only one output. In other words, there can’t be two different ???y???-values related to the same ???x???-value.
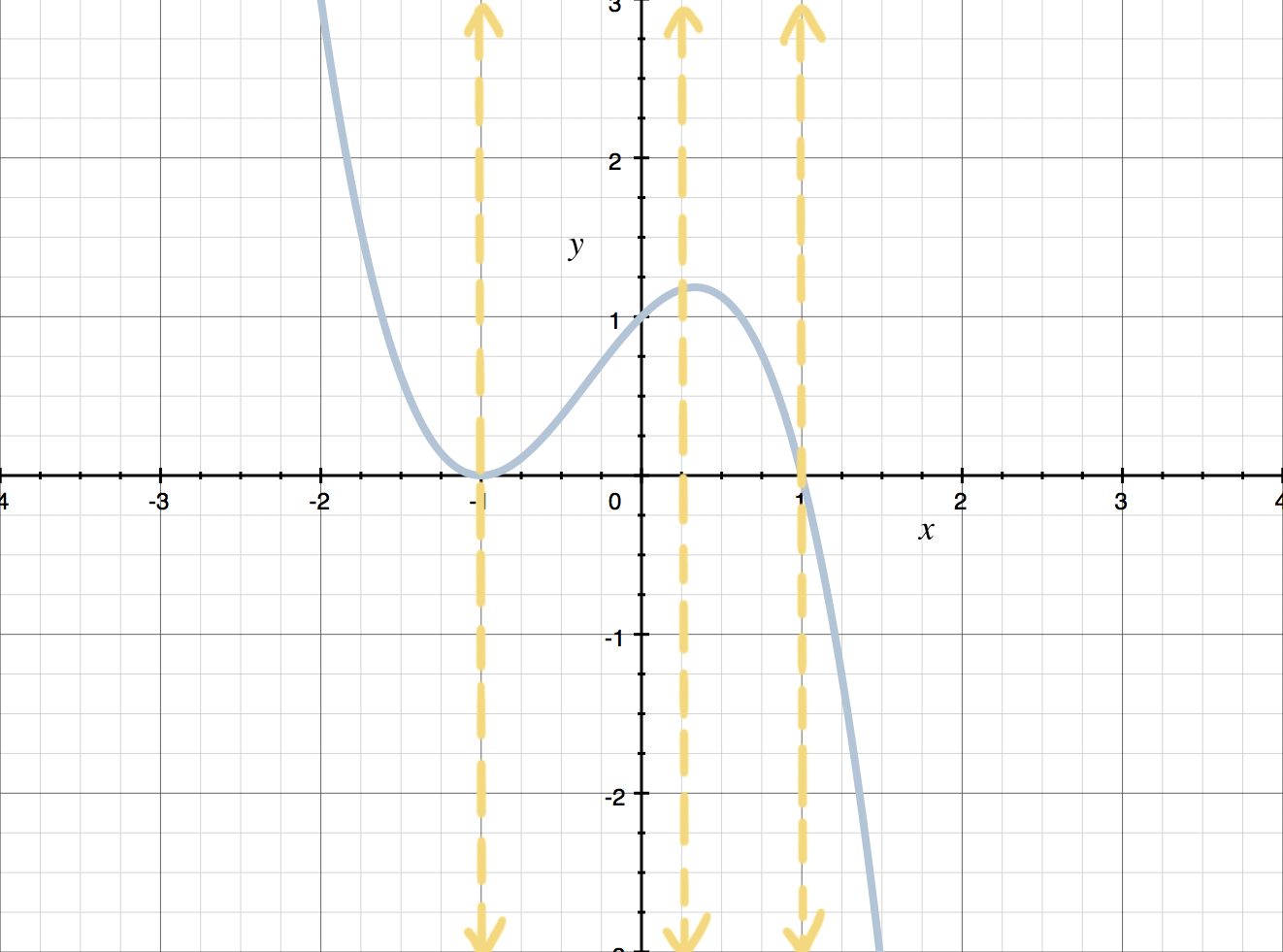
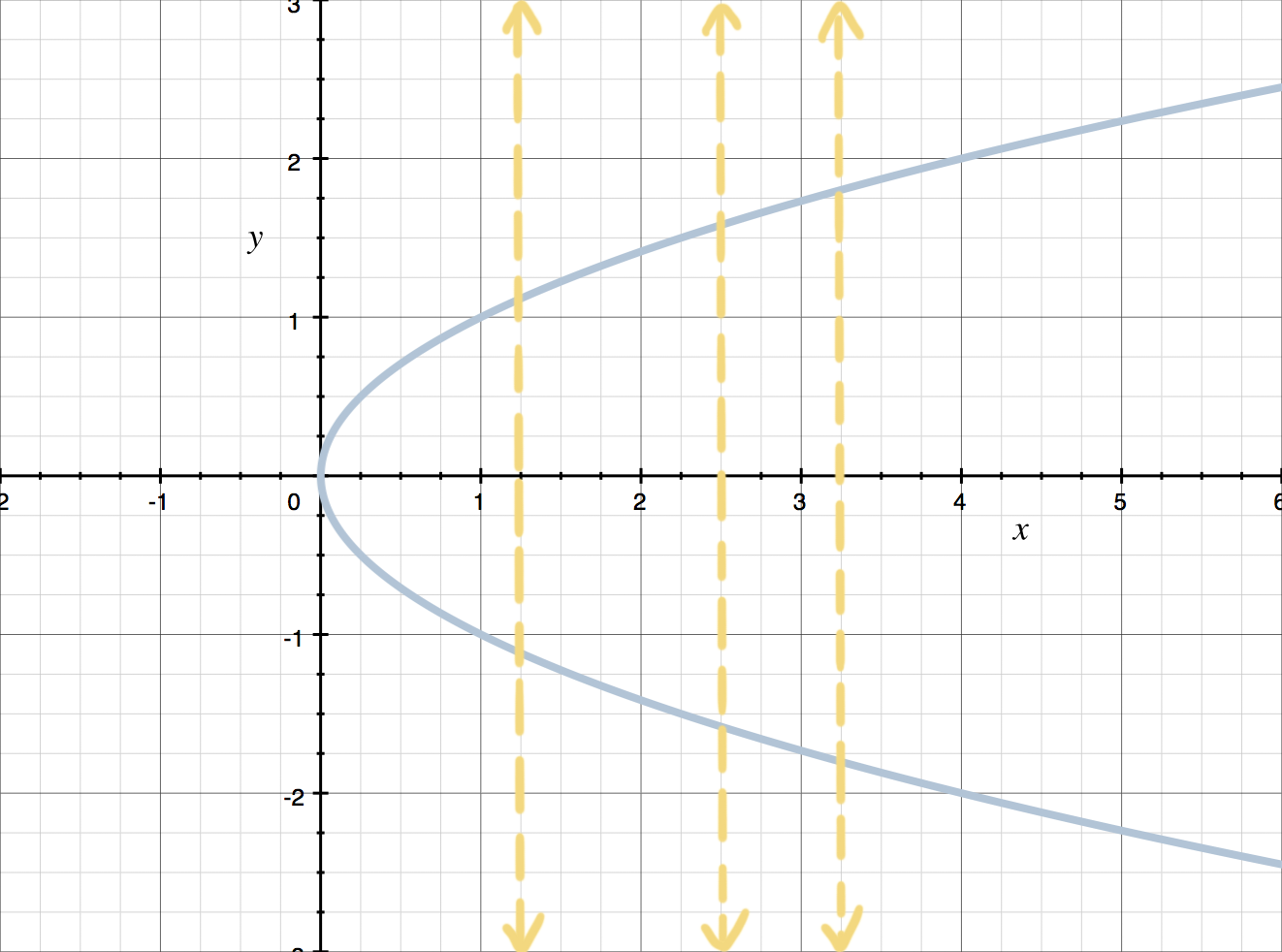
To test for functions, we need to make sure that there’s only one ???y???-value for every ???x???-value. Visually, when you look at the graph of a relation, you can see whether every ???x???-value is related to only one ???y???-value by using the Vertical Line Test: Any (and every possible) vertical line may intersect with (cross) the graph at most once. We say “at most once,” because even if the relation is a function, the vertical line that crosses the ???x???-axis at any number ???x??? that isn’t in the domain of the function won’t intersect the graph of the function at all. If some vertical line crosses the graph more than once, then the graph has failed the Vertical Line Test and the relation isn’t a function.
This graph passes the Vertical Line Test, so it does represent a function. Any vertical line will cross the graph at most once.
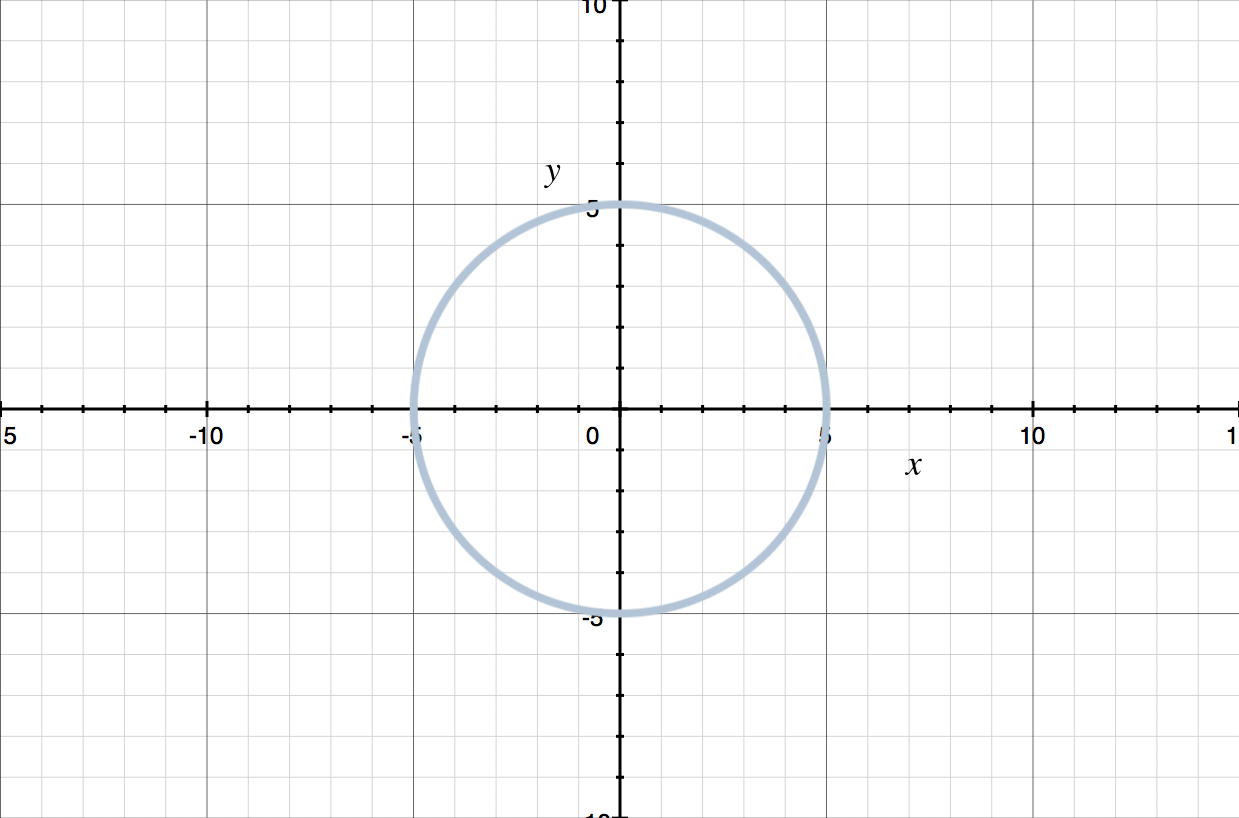
This graph doesn’t pass the Vertical Line Test, so it doesn’t represent a function. You can see that there are vertical lines that cross the graph twice.
How to identify functions
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
How to use the Vertical Line Test to verify whether a graph is a function
Example
Create a graph that represents a function and explain why it’s a function.
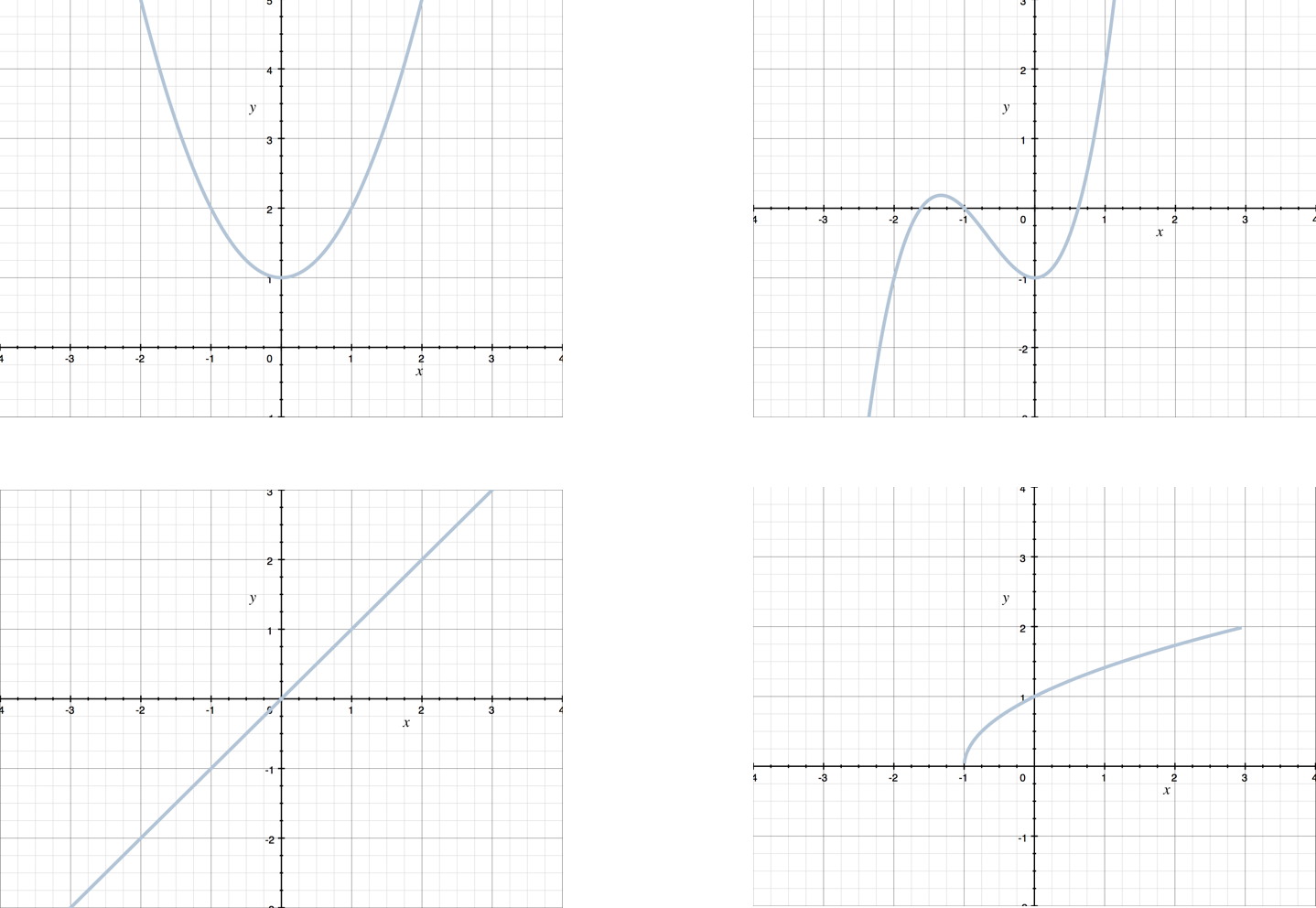
There are many different possibilities for this answer, but whatever graph you choose to draw must pass the Vertical Line Test. Any vertical line can touch the graph at most once. These are some examples of graphs of functions:
Let’s try another example of testing for functions.
Example
Which of the following three point sets could represent a function?
or
the relation whose graph consists of the points with coordinates ???(1,2)???, ???(2,4)???, ???(2,3)???
or
Only the last one,
can represent a function, because each input has only one output. This choice,
the relation whose graph consists of the points with coordinates ???(1,2)???, ???(2,4)???, and ???(2,3)???
isn’t a function, because the input ???2??? has both an output of ???3??? and an output of ???4???. And this choice,
doesn’t represent a function, because the graph doesn’t pass the Vertical Line Test (some vertical lines would cross the graph twice).