Using the addition rule, and union vs. intersection

What is the addition rule, and when does it apply?

Sometimes we’ll need to find the probability that two events occur together within one experiment. Remember that an event is a specific collection of outcomes from the sample space.

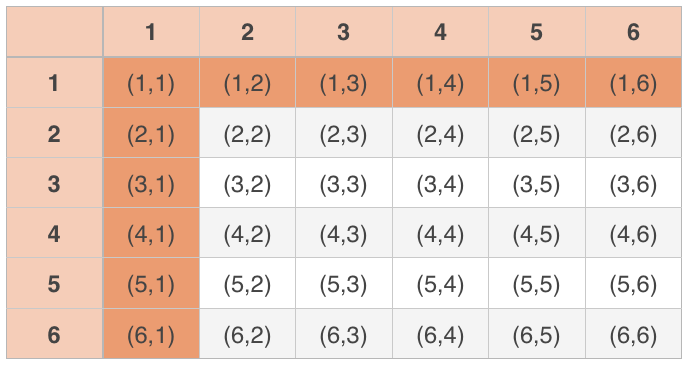
For example, what’s the probability that we roll a pair of $6$-sided dice and either get at least one $1$, or an even sum when we add the dice together?

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

When we roll two dice together, there are $36$ possible outcomes. There are $11$ rolls out of the $36$ where we get at least one $1$:

And there are $18$ possible outcomes where the sum of the dice is even.

So we might be tempted to say that the probability of getting at least one $1$ or an even sum is $P(1\text{ or even})=(11+18)/36$, or $29/36$. But we’ve neglected to consider that there’s some overlap between these two sets. We have the rolls $1-1$, $1-3$, $1-5$, $3-1$, and $5-1$ in both sets, so we’re double-counting those in our probability calculation.

Which means we have to subtract out the values that are overlapping. Since there are $5$ overlapping values, the probability calculation is actually

$P(1\text{ or even})=\frac{11+18-5}{36}$

$P(1\text{ or even})=\frac{24}{36}$

$P(1\text{ or even})=\frac23$

A great way to illustrate this kind of overlapping probability is with a Venn diagram. We would build a Venn diagram to show that there are $11$ rolls where we get at least one $1$, that there are $18$ rolls where the sum is even, and that there are $5$ rolls where we get at least one $1$ and the sum is also even.

Then, from the Venn diagram, we just add the $6+5=11$ and the $5+13=18$, and then subtract the overlapping $5$, in order to get all of the outcomes that meet our criteria, but without double-counting any of the outcomes. And then our probability again is

$P(1\text{ or even})=\frac{11+18-5}{36}=\frac{24}{36}=\frac23$

Addition rule

This idea of making sure that we don’t double-count the overlap is called the addition rule (or sum rule) for probability, and it’s given as:

$P(A \text{ or } B)=P(A)+P(B)-P(A\text{ and }B)$

Now what happens if there’s no overlap between $A$ and $B$? In that case, $A$ and $B$ are called mutually exclusive (or disjoint), and $P(A\text{ and }B)$ will be $0$. Which means the addition rule will simplify this way:

$P(A \text{ or } B)=P(A)+P(B)-P(A\text{ and }B)$

$P(A \text{ or } B)=P(A)+P(B)-0$

$P(A \text{ or } B)=P(A)+P(B)$

Which tells us that when events are mutually exclusive/disjoint, we can calculate the probability of either event $A$ happening or event $B$ happening simply by adding together the probability of each one happening individually.

For instance, the events in this Venn diagram are disjoint, since the circles don’t overlap:

Because there are $10+7=17$ total events, the probability of event $A$ is $P(A)=10/17$. And the probability of event $B$ is $P(B)=7/17$. So the probability that both events occur is

$P(A\text{ or }B)=P(A)+P(B)$

$P(A\text{ or }B)=\frac{10}{17}+\frac{7}{17}$

$P(A\text{ or }B)=\frac{17}{17}$

$P(A\text{ or }B)=1$

Union and intersection

In the first version of the addition rule formula, we use the words “or” and “and.” But we can also write the formula as:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

This second formula is the same addition rule calculation, but we use the $\cup$ and $\cap$ symbols instead of the words “and” and “or.”

$P(A\cup B)$ is called the union of $A$ and $B$, and it means the probability of either $A$ or $B$ or both occurring. $P(A\cap B)$ is called the intersection of $A$ and $B$, and it means the probability of  $A$ and $B$ both occurring.

Using the addition rule to calculate probability

---

Take the course

Want to learn more about Probability & Statistics? I have a step-by-step course for that. :)

---

Using the addition rule to calculate probabilities from a two-way data table

Example

We surveyed $100$ people about their favorite sport, and recorded their gender and favorite sport in a table.

1. What is the probability that a participant is male?

2. What is the probability that a participant’s favorite sport is football?

3. What is the probability that a participant is female or prefers a sport other than football or basketball?

We know from the table that $60$ of the $100$ participants are male, so the probability that a participant is male is

$P(\text{male})=\frac{60}{100}=\frac35$

And from the table we can see that $38$ of the $100$ participants like football best, so the probability that a participant’s favorite sport is football is

$P(\text{football})=\frac{38}{100}=\frac{19}{50}$

This idea of making sure that we don’t double-count the overlap is called the addition rule (or sum rule) for probability.

These were both simple probability questions, but the third question requires us to use the addition rule. There are $40$ female participants, and $41$ participants who prefer a sport other than football or basketball.

But there are $16$ participants in the “overlap” group: the group of females who also prefer a sport other than football or basketball. Therefore, we’ll apply the addition rule and say that the probability that a participant is female or likes a sport other than football and basketball is

$P(\text{female or other})=\frac{40+41-16}{100}=\frac{65}{100}=\frac{13}{20}$

---

Get access to the complete Probability & Statistics course

---