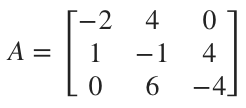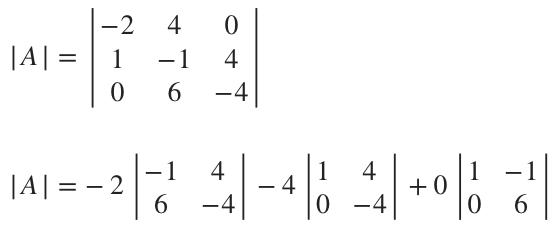Finding the transpose of a matrix and then finding its determinant
Defining the transpose of a matrix
In this lesson, we want to start talking about matrix transposes.
The transpose of a matrix is simply the matrix you get when you swap all the rows and columns. In other words, the first row becomes the first column, the second row becomes the second column, and the ???n???th row becomes the ???n???th column.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
You can find the transpose of any matrix with any dimensions, and we indicate the transpose of an ???m\times n??? matrix ???A??? as an ???n\times m??? matrix ???A^T???, and we call it “A transpose.”
How to find the transpose of a matrix, and then find the determinant of that transpose
Take the course
Want to learn more about Linear Algebra? I have a step-by-step course for that. :)
Example of finding the transpose matrix
Example
Find the transpose of ???A???.
The first row of ???A??? is ???\begin{bmatrix}-2\ \ 4\ \ 0\end{bmatrix}???, so this sequence of entries needs to become the first column of ???A^T???.
The second row of ???A??? is ???\begin{bmatrix}1\ \ -1\ \ 4\end{bmatrix}???, so this sequence of entries needs to become the second column of ???A^T???.
The third row of ???A??? is ???\begin{bmatrix}0\ \ 6\ \ -4\end{bmatrix}???, so this sequence of entries needs to become the third column of ???A^T???.
This works for non-square matrices, too. So the transpose of a matrix
is
It’s also important to realize that the transpose of a transpose gets you back to the original matrix. So given matrix ???A??? and the transpose of matrix ???A^T???, then ???(A^T)^T=A???.
Determinant of the transpose
The determinant of a transpose of a square matrix will always be equal to the determinant of the original matrix. In other words, given an ???n\times n??? matrix ???A???, the determinant of ???A??? and the determinant of ???A^T??? are equivalent.
The determinant of a transpose of a square matrix will always be equal to the determinant of the original matrix.
Example
Show that the determinants of ???A??? and ???A^T??? are equivalent.
The determinant of ???A??? is
The last term gets zeroed out.
???|A|=-2((-1)(-4)-(4)(6))-4((1)(-4)-(4)(0))+0((1)(6)-(-1)(0))???
???|A|=-2(4-24)-4(-4-0)+0(6-0)???
???|A|=-2(-20)-4(-4)+0(6)???
???|A|=40+16+0???
???|A|=56???
The matrix ???A^T??? is
The determinant of ???A^T??? is
The last term gets zeroed out.
???|A^T|=-2((-1)(-4)-(6)(4))-1((4)(-4)-(6)(0))+0((4)(4)-(-1)(0))???
???|A^T|=-2(4-24)-1(-16-0)+0(16-0)???
???|A^T|=-2(-20)-1(-16)+0(16)???
???|A^T|=40+16+0???
???|A^T|=56???
So we’ve shown that the determinants of ???A??? and ???A^T??? are equivalent.
???|A|=|A^T|=56???