Transversals, and their special angle pairs

There are lots of special angle pairs created when a transversal crosses two lines

In this lesson we’ll look at the angles formed when a pair of parallel lines is crossed by another line, called a “transversal.”

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Transversals

A transversal is a line that crosses at least two other lines.

Special angle pairs

When transversals cross parallel lines, they form angles with special angle relationships. The angle pair relationships form two types of special angles.

Congruent angles have the same measure.

Supplementary angles have measures that add up to $180{}^\circ$.

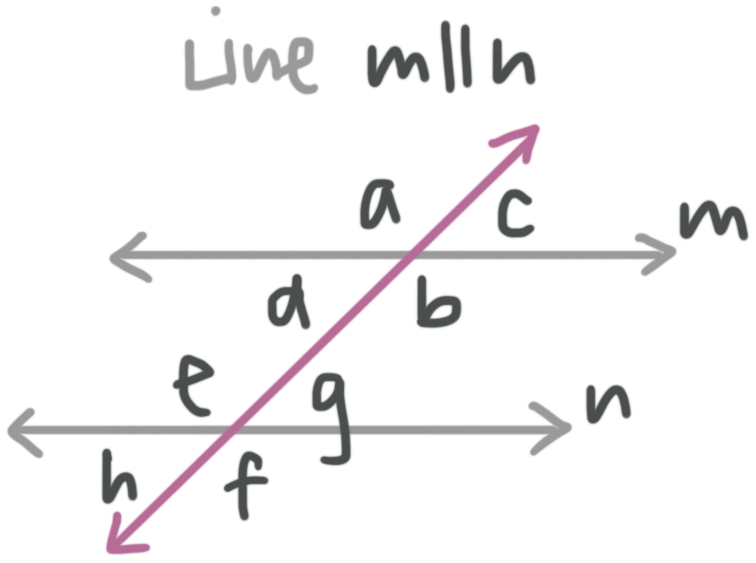
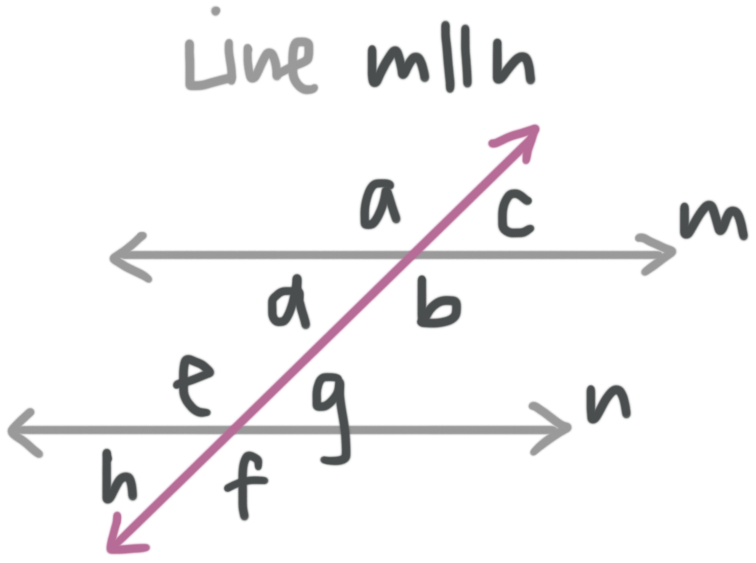
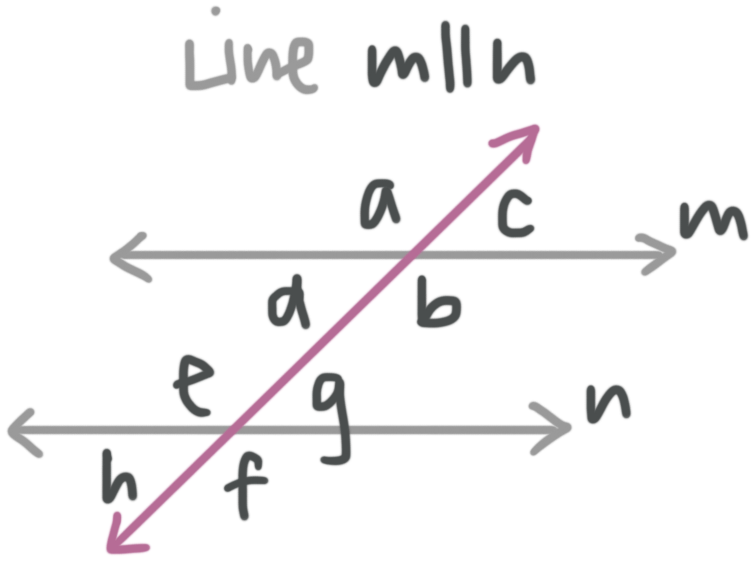
Types of special angle pairs

Vertical angles share a vertex, but lie on opposite sides of both the parallel lines and the transversal. Vertical angle pairs are congruent.

$m\angle a=m\angle b$

$m\angle c=m\angle d$

$m\angle e=m\angle f$

$m\angle g=m\angle h$

Corresponding angles are matching angles that lie, one on each parallel line, on the same side of the parallel lines and the same side of the transversal. Corresponding angle pairs are congruent.

$m\angle a=m\angle e$

$m\angle d=m\angle h$

$m\angle c=m\angle g$

$m\angle b=m\angle f$

Alternate interior angles are angles that lie, one on each line, on opposite sides of the parallel lines and opposite sides of the transversal, inside of the parallel lines. Alternate interior angle pairs are congruent.

$m\angle d=m\angle g$

$m\angle b=m\angle e$

Alternate exterior angles are angles that lie, one on each line, on opposite sides of the parallel lines and opposite sides of the transversal, outside of the parallel lines. Alternate exterior angle pairs are congruent.

$m\angle a=m\angle f$

$m\angle c=m\angle h$

Consecutive interior angles are angles that lie, one on each parallel line, on opposite sides of the parallel lines, but on the same side of the transversal. Consecutive interior angle pairs are supplementary, which means they sum to $180^\circ$.

$m\angle d+m\angle e=180{}^\circ$

$m\angle b+m\angle g=180{}^\circ$

Adjacent angles are angles with the same vertex that lie on opposite sides of the parallel line, but on the same side of the transversal. Adjacent angle pairs are supplementary, which means they sum to $180^\circ$.

$m\angle a+m\angle d=180{}^\circ$

$m\angle a+m\angle c=180{}^\circ$

$m\angle b+m\angle c=180{}^\circ$

$m\angle d+m\angle b=180{}^\circ$

$m\angle e+m\angle g=180{}^\circ$

$m\angle e+m\angle h=180{}^\circ$

$m\angle g+m\angle f=180{}^\circ$

$m\angle f+m\angle h=180{}^\circ$

We often use these angle pair relationships to solve problems.

Working with the angles created by a transversal

---

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

---

An example with corresponding and adjacent angle pairs

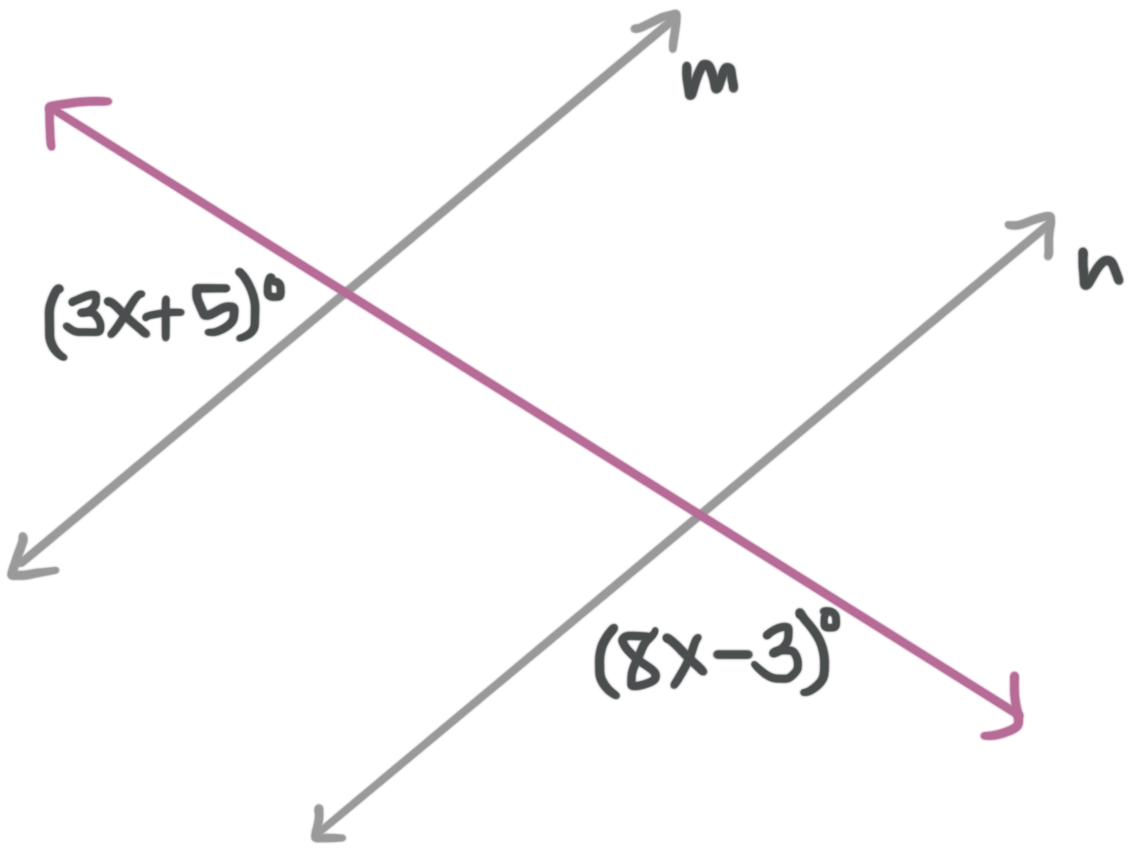
Example

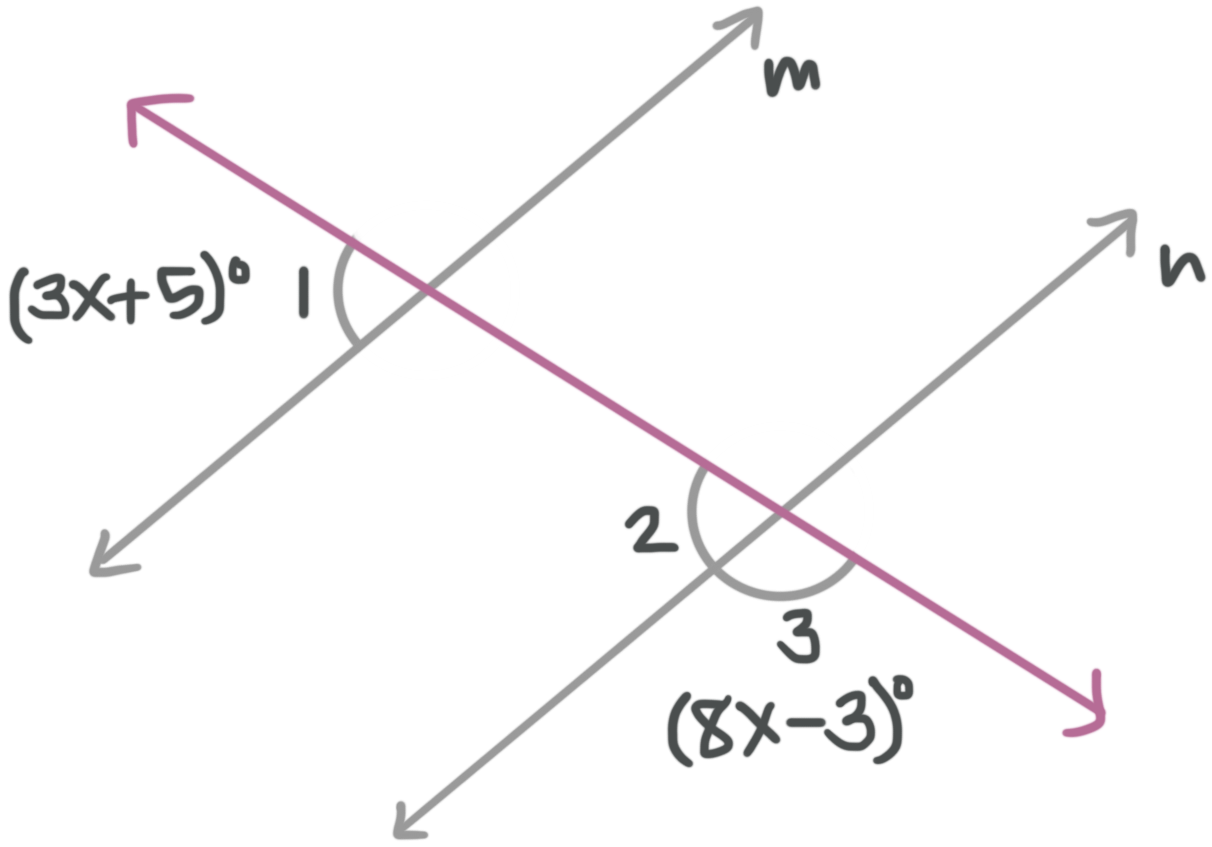
Solve for the variable. Find the value of $x$ to the nearest tenth, given $m||n$.

We can think of which angle pair relationships to use.

Angles $\angle 1$ and $\angle 2$ are congruent because they are a corresponding angle pair. Angles $\angle 2$ and $\angle 3$ are supplementary because they are adjacent angles. This means the two angles with variables are supplementary, so

$(3x+5){}^\circ +(8x-3){}^\circ =180{}^\circ$

$3x{}^\circ +5{}^\circ +8x{}^\circ -3{}^\circ =180{}^\circ$

$11x{}^\circ +2{}^\circ =180{}^\circ$

$11x{}^\circ =178{}^\circ$

$x\approx 16.2{}^\circ$

When transversals cross parallel lines, they form angles with special angle relationships. The angle pair relationships form two types of special angles.

Example

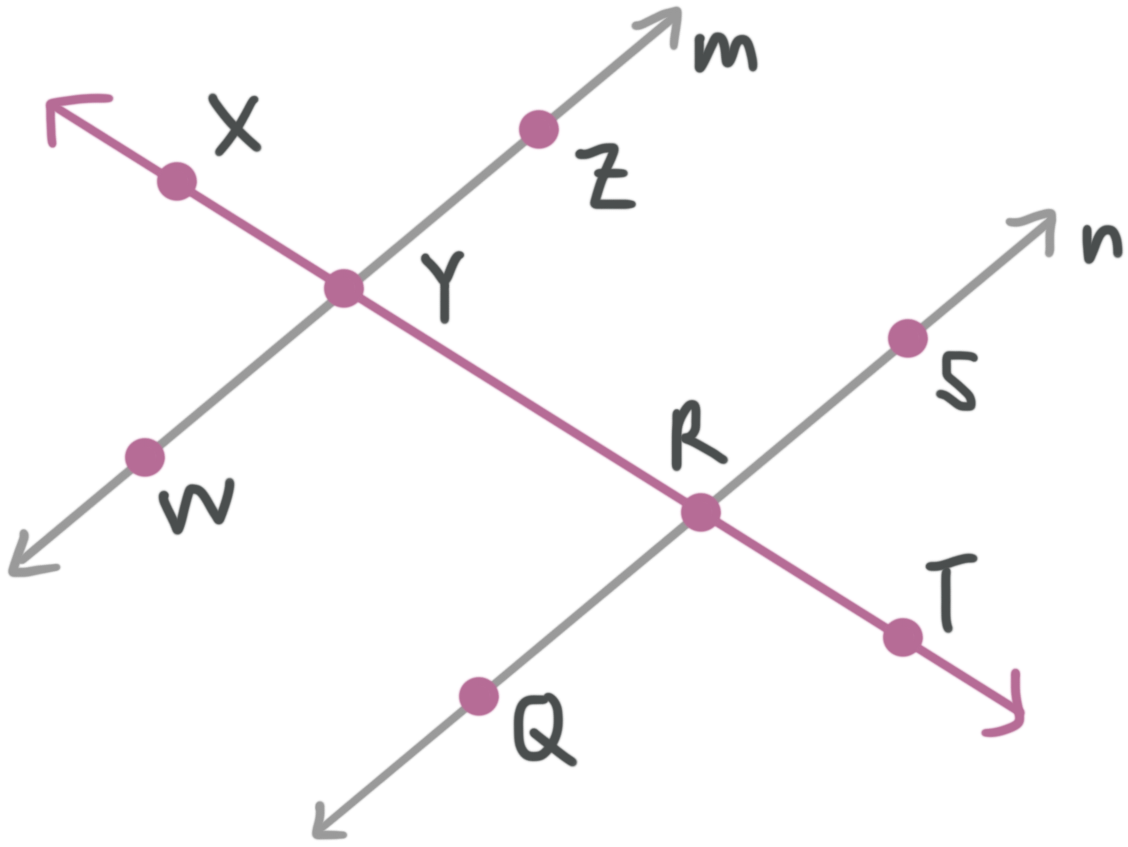
What is the measure of $\angle XYZ$, given $m||n$, $m\angle ZYR=(5x+35){}^\circ$ and $m\angle QRY=(15x-5){}^\circ$?

Looking at the diagram, we can see that $\angle XYZ$ and $\angle ZYR$ are adjacent angles that lie on the same parallel line, so they’re supplementary. $\angle ZYR$ and $\angle QYR$ are alternate interior angles, so they’re congruent.

Now we can use these facts to find the $m\angle XYZ$. Let’s begin by solving for $x$. $m\angle ZYR=m\angle QYR$ because they are congruent angles. So,

$m\angle ZYR=m\angle QYR$

$(5x+35){}^\circ =(15x-5){}^\circ$

$35{}^\circ =10x{}^\circ -5{}^\circ$

$40{}^\circ =10x{}^\circ$

$x=4{}^\circ$

Now we can find $m\angle ZYR$ when $x=4{}^\circ$.

$m\angle ZYR=(5x+35){}^\circ$

$m\angle ZYR=(5\cdot 4+35){}^\circ$

$m\angle ZYR=(20+35){}^\circ$

$m\angle ZYR=55^\circ$

And because $\angle XYZ$ and $\angle ZYR$ are supplementary angles,

$m\angle XYZ+m\angle ZYR=180{}^\circ$

$m\angle XYZ+55{}^\circ =180{}^\circ$

$m\angle XYZ+55{}^\circ -55{}^\circ =180{}^\circ -55{}^\circ$

$m\angle XYZ=125{}^\circ$

---

Get access to the complete Geometry course

---