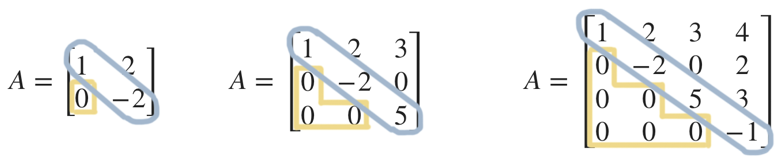Upper and lower triangular matrices

What are upper triangular matrices and lower triangular matrices?

Upper triangular matrices are matrices in which all entries below the main diagonal are $0$. The main diagonal is the set of entries that run from the upper left-hand corner of the matrix down to the lower right-hand corner of the matrix.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

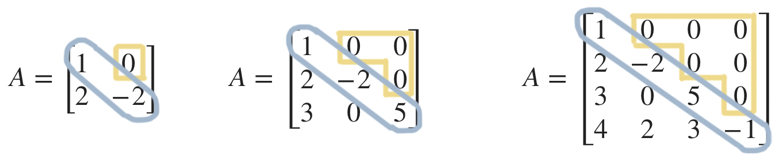
Lower triangular matrices are matrices in which all entries above the main diagonal are $0$.

Here are the main diagonals in these upper triangular matrices,

and in these lower triangular matrices:

We’ve circled the main diagonal in each matrix, so that we can see that all of the entries in the upper triangular matrix below the main diagonal are $0$, and that all of the entries in the lower triangular matrix above the main diagonal are $0$.

Determinant of triangular matrices

Because we can find the determinant of a matrix along any row or column that we’d like, for upper triangular matrices, you’d always want to choose the first column (or last row), since it includes the most $0$ entries.

For instance, let’s say we want to find the determinant of the upper triangular matrix $A$:

Notice that $A$ includes a $0$ entry in $a_{(2,3)}$. That’s okay. We can have zero values on or above the main diagonal. To be considered an upper triangular matrix, the only thing that matters is that all the entries below the main diagonal are $0$.

The determinant of $A$ along the first column is

The last three terms get zeroed out.

Let’s simplify the remaining $3\times3$ determinant along the first column again.

The last two terms get zeroed out.

$|A|=1\left[-2((5)(-1)-(3)(0))\right]$

$|A|=1\left[(-2)(5)(-1)\right]$

$|A|=(1)(-2)(5)(-1)$

$|A|=10$

We want to notice two things about this result.

First, the calculation was much easier than a typical $4\times4$ determinant, so working along the first column is a good strategy when we’re calculating an upper triangular matrix determinant.

Second, the value of the determinant was the product $(1)(-2)(5)(-1)$, which is the product of all the entries in the main diagonal of $A$.

In fact, for all upper triangular matrices, this will always be true! Given any upper triangular matrix, you can find the value of the determinant simply by multiplying together all of the entries along the main diagonal of the matrix. This also tells you that, if you have a $0$ anywhere along the main diagonal of an upper triangular matrix, that the determinant will be $0$. Which means that if the matrix contains a full row of zeros, anywhere in the matrix, that the determinant will be $0$.

The same is true for lower triangular matrices. If you were calculating the determinant traditionally, you’d want to calculate it along the first row or last column, since those include the most $0$ entries.

If you did that, you’d find the determinant of the lower triangular matrix to be the product of the entries along the main diagonal, just like we did for upper triangular matrices.

Putting a matrix into upper triangular form or lower triangular form is actually a great way to find the determinant quickly.

Defining and building upper triangular matrices and lower triangular matrices

---

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

---

Putting the matrix into triangular form

Example

Put $A$ into upper or lower triangular form to find the determinant.

In $A$, we don’t have any more zeros below the main diagonal than above it, or vice versa, so we could really work in either direction. Let’s start by rewriting the matrix as the determinant we’re trying to find.

Now switch the first and second rows so that we have a pivot entry in the first row. Remember that when we switch rows, the determinant gets multiplied by $-1$.

The main diagonal is the set of entries that run from the upper left-hand corner of the matrix down to the lower right-hand corner of the matrix.

Now let’s perform $2R_1+R_2\to R_2$.

Now perform $-3R_2+R_3\to R_3$.

Now that we’ve got $A$ in upper triangular form, the determinant is just the product of the entries along the main diagonal. Don’t forget the negative sign in front of the matrix that we put in for the row switch.

$|A|=-(1)(2)(-28)$

$|A|=56$

---

Get access to the complete Linear Algebra course

---