Finding the acute angle between two lines (or between two vectors)
What is an acute angle?
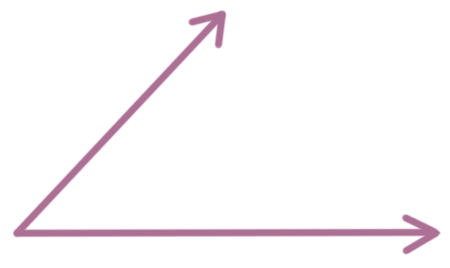
An acute angle is an angle that’s less than ???90^\circ???, like this:
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
If we want to find the acute angle between two lines, we can convert the lines to standard vector form and then use the formula
???\cos{\theta}=\frac{a\cdot b}{|a||b|}???
where ???a??? and ???b??? are the given vectors, ???a\cdot{b}??? is the dot product of the vectors, ???|a|??? is the magnitude of the vector ???a??? (its length) and ???|b|??? is the magnitude of the vector ???b??? (its length). We can find the magnitude of both vectors using the distance formula
???D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}???
for a two-dimensional vector where the point ???(x_1,y_1)??? is the origin ???(0,0)???.
If the formula above gives a result that’s greater than ???90^\circ???, then we’ve found the obtuse angle between the lines. To find the acute angle, we just subtract the obtuse angle from ???180^\circ???, and we’ll get the acute angle.
How do we find the acute angle between two lines, when the lines are defined by vectors?
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Converting lines into vectors, then finding the angle between those two vectors
Example
Find the acute angle between the lines.
???x+3y=2???
???3x-6y=5???
First we’ll convert the lines to standard vector form.
???x+3y=2???
???a=\langle1,3\rangle???
and
???3x-6y=5???
???b=\langle3,-6\rangle???
Before we can use our formula, we need to find the dot product of ???a??? and ???b???.
???a\cdot{b}=(1)(3)+(3)(-6)???
???a\cdot{b}=3-18???
???a\cdot{b}=-15???
Now we need to find the length of each vector using the distance formula.
???|a|=\sqrt{(1-0)^2+(3-0)^2}???
???|a|=\sqrt{1+9}???
???|a|=\sqrt{10}???
and
???|b|=\sqrt{(3-0)^2+(-6-0)^2}???
???|b|=\sqrt{9+36}???
???|b|=\sqrt{45}???
If we want to find the acute angle between two lines, we can convert the lines to standard vector form.
Plugging ???a\cdot{b}=-15???, ???|a|=\sqrt{10}???, and ???|b|=\sqrt{45}??? into the formula, we get
???\cos{\theta}=\frac{-15}{\sqrt{10}\sqrt{45}}???
???\cos{\theta}=\frac{-15}{\sqrt{450}}???
???\cos{\theta}=\frac{-15}{\sqrt{450}}???
???\cos{\theta}=\frac{-15}{\sqrt{225\cdot2}}???
???\cos{\theta}=\frac{-15}{15\sqrt{2}}???
???\cos{\theta}=\frac{-1}{\sqrt{2}}???
Rationalize the denominator.
???\cos{\theta}=\frac{-1}{\sqrt{2}}\left(\frac{\sqrt{2}}{\sqrt{2}}\right)???
???\cos{\theta}=\frac{-\sqrt{2}}{2}???
Looking at the top half of the unit circle, we can see that
???\theta=\frac{3\pi}{4}=135^\circ???
Since the answer is greater than ???90^\circ???, we’ve found the obtuse angle between the lines. To find the acute angle, we’ll just subtract this value from ???180^\circ???.
???\theta=180^\circ-135^\circ???
???\theta=45^\circ???
The acute angle between the lines is ???45^\circ???.