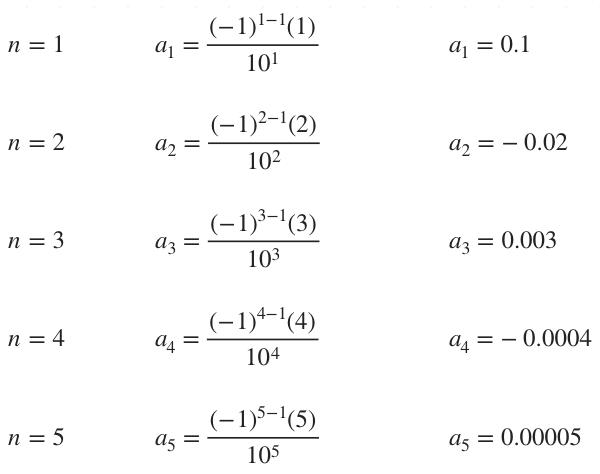The alternating series estimation theorem to estimate the value of the series and state the error

Using the alternating series estimation theorem requires us to follow two rules

The alternating series estimation theorem gives us a way to approximate the sum of an alternating series with a remainder or error that we can calculate.

To use this theorem, our series must follow two rules:

1. The series must be decreasing, $b_n\geq b_{n+1}$

2. The limit of the series must be zero, $\lim_{n\to\infty}b_n=0$

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Once we confirm that our alternating series meets these two conditions, we can calculate the error using

$|R_n|=|s-s_n|\le{b_{n+1}}$

How to calculate the error using alternating series estimation

---

Take the course

Want to learn more about Calculus 2? I have a step-by-step course for that. :)

---

Using the alternating series estimation theorem to approximate the alternating series to three decimal places

Example

Approximate the sum of the series to three decimal places.

$\sum^{\infty}_{n=1}\frac{(-1)^{n-1}n}{10^n}$

We’ll calculate the first few terms of the series until we have a stable answer to three decimal places.

Next, we need to sum these terms until we can see that the third decimal place isn’t changing.

Adding the first two terms together, we get

$a_1+a_2=0.1+(-0.02)$

$a_1+a_2=0.1-0.02$

$a_1+a_2=0.08$

$s_2=0.08$

Since we’re not to three decimal places, we’ll add another term to the sum

$a_1+a_2+a_3=0.1+(-0.02)+0.003$

$a_1+a_2+a_3=0.1-0.02+0.003$

$a_1+a_2+a_3=0.083$

$s_3=0.083$

We’ve made it to three decimal places, but we need to make sure that the fourth decimal place won’t cause the third decimal place to round up.

$a_1+a_2+a_3+a_4=0.1+(-0.02)+0.003+(-0.0004)$

$a_1+a_2+a_3+a_4=0.1-0.02+0.003-0.0004$

$a_1+a_2+a_3+a_4=0.0826$

$s_4=0.0826$

Now we know that the fourth decimal place is going to cause us to round up the third decimal place, and our approximation to three decimal places is

$s_3\approx0.083$

In order to use the alternating series estimation theorem, we need to show that the series is decreasing, ${b_n}\geq b_{n+1}$. Pulling out $b_n$ from the given series, we get

$b_n=\frac{n}{10^n}$

Which means that

$b_{n+1}=\frac{n+1}{10^{n+1}}$

Now we can calculate the first three terms for both $b_n$ and $b_{n+1}$.

The alternating series estimation theorem gives us a way to approximate the sum of an alternating series with a remainder or error that we can calculate.

Looking at these results, we can see that ${b_n}\geq b_{n+1}$, so $b_n$ is decreasing.

Next, we need to show that $\lim_{n\to\infty}b_n=0$.

$\lim_{n\to\infty}\frac{n}{10^n}$

When we evaluate $b_n$ as it approaches infinity, we can see that the denominator will increase much faster than the numerator. This means that the fraction will approach $0$.

$\lim_{n\to\infty}\frac{n}{10^n}=0$

Now that we’ve shown that our series meets the two criteria, we can use the alternating series estimation theorem. We’ll use the inequality

$|R_n|=|s-s_n|\le{b_{n+1}}$

Plugging in the values we have, we get

$|R_3|=|s-s_3|\le{b_{3+1}}$

$|R_3|\le{b_4}$

$|R_3|\le\frac{4}{10^4}$

$|R_3|\le\frac{1}{2,500}$

$|R_3|\le0.0004$

The approximate sum of the series to three decimal places is $0.083$ with an error of $|R_3|\le0.0004$.

---

Get access to the complete Calculus 2 course

---