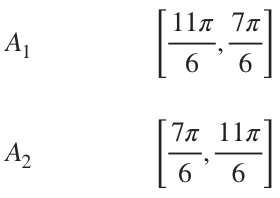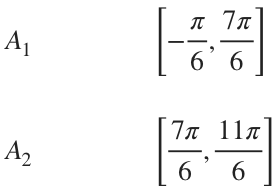Calculating the area between polar curves

Five steps for finding the area between polar curves

In order to calculate the area between two polar curves, we’ll

1. Find the points of intersection if the interval isn’t given

2. Graph the curves to confirm the points of intersection

3. For each enclosed region, use the points of intersection to find upper and lower limits of integration $[\alpha,\beta]$

4. For each enclosed region, determine which curve is the outer curve and which is the inner

5. Plug this into the formula for area between curves,

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

$A=\int^{\beta}_{\alpha}\frac12\left(r^2_O-r^2_I\right)\ d\theta$

where $[\alpha,\beta]$ is the interval that defines the area

where $r_O$ is the outer curve

where $r_I$ is the inner curve

Video example of how to calculate the area enclosed by two polar curves

---

Take the course

Want to learn more about Calculus 2? I have a step-by-step course for that. :)

---

Finding the area between two polar curves

Example

Find the area between the polar curves.

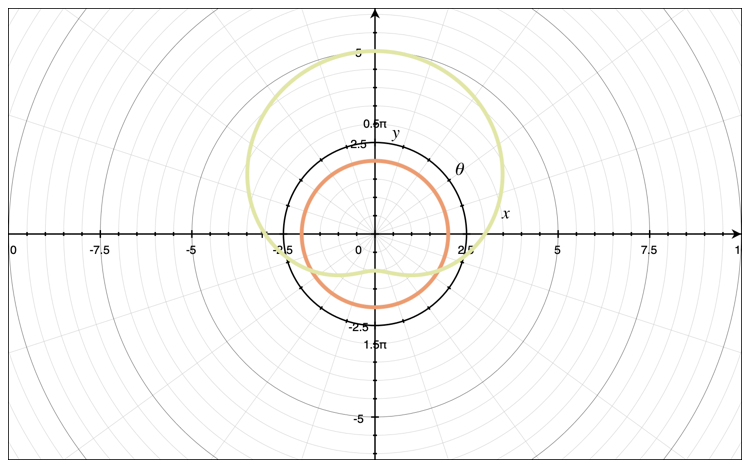
1. $r=2$

2. $r=3+2\sin{\theta}$

Since the problem doesn’t give us an interval over which to evaluate the area, we’ll need to find the points of intersection of the curves. We’ll set the polar curves equal to each other and solve for $\theta$.

$3+2\sin{\theta}=2$

$\sin{\theta}=-\frac12$

$\theta=\frac{7\pi}{6},\ \frac{11\pi}{6}$

We’ll graph the curves to confirm the points of intersection.

Based on the graph above, the area between curves is given by

$A_T=A_1+A_2$

where $A_T$ is total area

where $A_1$ is the larger section

where $A_2$ is the smaller section

We always want to work in a counterclockwise direction, which means that, in order to find $A_1$ and $A_2$, we’ll use the intervals

However, we always need $\alpha<\beta$ in our interval, so we’ll change the interval for $A_1$ into its equivalent $-\theta$, and we’ll get

We’ll also need to use the graph to indicate which curve is the outer curve and which is the inner curve. We’ll say

Now we can plug everything we’ve found into the area formula.

$A_T=A_1+A_2$

$A_T=\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}\frac12\left[\left(3+2\sin{\theta}\right)^2-(2)^2\right]\ d\theta+\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}\frac12\left[(2)^2-\left(3+2\sin{\theta}\right)^2\right]\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}\left(3+2\sin{\theta}\right)\left(3+2\sin{\theta}\right)-4\ d\theta+\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}4-\left(3+2\sin{\theta}\right)\left(3+2\sin{\theta}\right)\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}9+12\sin{\theta}+4\sin^2{\theta}-4\ d\theta+\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}4-\left(9+12\sin{\theta}+4\sin^2{\theta}\right)\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}4\sin^2{\theta}+12\sin{\theta}+5\ d\theta+\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}4-9-12\sin{\theta}-4\sin^2{\theta}\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}4\sin^2{\theta}+12\sin{\theta}+5\ d\theta-\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}4\sin^2{\theta}+12\sin{\theta}+5\ d\theta$

Since $2\sin^2{\theta}=1-\cos{(2\theta)}$,

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}2\left[1-\cos{(2\theta)}\right]+12\sin{\theta}+5\ d\theta-\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}2\left[1-\cos{(2\theta)}\right]+12\sin{\theta}+5\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}2-2\cos{(2\theta)}+12\sin{\theta}+5\ d\theta-\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}2-2\cos{(2\theta)}+12\sin{\theta}+5\ d\theta$

$A_T=\frac12\int_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}12\sin{\theta}-2\cos{(2\theta)}+7\ d\theta-\frac12\int_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}12\sin{\theta}-2\cos{(2\theta)}+7\ d\theta$

$A_T=\frac12\left[-12\cos{\theta}-\sin{(2\theta)}+7\theta\right]\bigg|_{-\frac{\pi}{6}}^{\frac{7\pi}{6}}-\frac12\left[-12\cos{\theta}-\sin{(2\theta)}+7\theta\right]\bigg|_{\frac{7\pi}{6}}^{\frac{11\pi}{6}}$

Since the problem doesn’t give us an interval over which to evaluate the area, we’ll need to find the points of intersection of the curves.

Evaluate over the interval.

$A_T=\frac12\left[-12\cos{\frac{7\pi}{6}}-\sin{\frac{14\pi}{6}}+7\left(\frac{7\pi}{6}\right)-\left[-12\cos{\left(-\frac{\pi}{6}\right)}-\sin{\left(-\frac{2\pi}{6}\right)}+7\left(-\frac{\pi}{6}\right)\right]\right]$

$-\frac12\left[-12\cos{\frac{11\pi}{6}}-\sin{\frac{22\pi}{6}}+7\left(\frac{11\pi}{6}\right)-\left[-12\cos{\frac{7\pi}{6}}-\sin{\frac{14\pi}{6}}+7\left(\frac{7\pi}{6}\right)\right]\right]$

$A_T=\frac12\left[-12\cos{\frac{7\pi}{6}}-\sin{\frac{7\pi}{3}}+\frac{49\pi}{6}-\left(-12\cos{\frac{11\pi}{6}}-\sin{\frac{5\pi}{6}}-\frac{7\pi}{6}\right)\right]$

$-\frac12\left[-12\cos{\frac{11\pi}{6}}-\sin{\frac{11\pi}{3}}+\frac{77\pi}{6}-\left(-12\cos{\frac{7\pi}{6}}-\sin{\frac{7\pi}{3}}+\frac{49\pi}{6}\right)\right]$

$A_T=\frac12\left(-12\cos{\frac{7\pi}{6}}-\sin{\frac{7\pi}{3}}+\frac{49\pi}{6}+12\cos{\frac{11\pi}{6}}+\sin{\frac{5\pi}{6}}+\frac{7\pi}{6}\right)$

$-\frac12\left(-12\cos{\frac{11\pi}{6}}-\sin{\frac{11\pi}{3}}+\frac{77\pi}{6}+12\cos{\frac{7\pi}{6}}+\sin{\frac{7\pi}{3}}-\frac{49\pi}{6}\right)$

$A_T=\frac12\left(-12\cos{\frac{7\pi}{6}}-\sin{\frac{7\pi}{3}}+12\cos{\frac{11\pi}{6}}+\sin{\frac{5\pi}{6}}+\frac{28\pi}{3}\right)$

$-\frac12\left(-12\cos{\frac{11\pi}{6}}-\sin{\frac{11\pi}{3}}+12\cos{\frac{7\pi}{6}}+\sin{\frac{7\pi}{3}}+\frac{14\pi}{3}\right)$

Simplify the trigonometric functions.

$A_T=\frac12\left[-12\left(-\frac{\sqrt{3}}{2}\right)-\frac{\sqrt{3}}{2}+12\left(\frac{\sqrt{3}}{2}\right)+\frac12+\frac{28\pi}{3}\right]$

$-\frac12\left[-12\left(\frac{\sqrt{3}}{2}\right)-\left(-\frac{\sqrt{3}}{2}\right)+12\left(\frac{\sqrt{3}}{2}\right)+\frac{\sqrt{3}}{2}+\frac{14\pi}{3}\right]$

$A_T=\frac12\left(\frac{6\sqrt{3}}{2}-\frac{\sqrt{3}}{2}+\frac{12\sqrt{3}}{2}+\frac12+\frac{28\pi}{3}\right)-\frac12\left(-\frac{12\sqrt{3}}{2}+\frac{\sqrt{3}}{2}+\frac{12\sqrt{3}}{2}+\frac{\sqrt{3}}{2}+\frac{14\pi}{3}\right)$

$A_T=\frac12\left(\frac{1+17\sqrt{3}}{2}+\frac{28\pi}{3}\right)-\frac12\left(\frac{2\sqrt{3}}{2}+\frac{14\pi}{3}\right)$

$A_T=\frac{1+17\sqrt{3}}{4}+\frac{28\pi}{6}-\frac{2\sqrt{3}}{4}-\frac{14\pi}{6}$

$A_T=\frac{1+15\sqrt{3}}{4}+\frac{14\pi}{6}$

$A_T=\frac{1+15\sqrt{3}}{4}+\frac{7\pi}{3}$

Find a common denominator.

$A_T=\frac{3+45\sqrt{3}}{12}+\frac{28\pi}{12}$

$A_T=\frac{28\pi+45\sqrt{3}+3}{12}$

---

Get access to the complete Calculus 2 course

---