Using laws of natural logs
Log laws equivalently apply to natural logs
All of these rules that we’ve just learned for manipulating logarithms also apply to natural logs.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
General rule for logs
The general rule for natural logs is:
Given the exponential equation ???e^x=y???,
the associated logarithmic equation is ???\log_e{(y)}=x???,
and vice versa.
Of course, ???\log_e??? is the same as the natural log, ???\ln???. So we can rewrite the general rule for natural logs:
Given the exponential equation ???e^x=y???,
the associated logarithmic equation is ???\ln{(y)}=x???,
and vice versa.
Product rule
The product rule for logs is
???\log_a(xy)=\log_ax+\log_ay???
In terms of natural logarithms, this same rule is
???\ln(xy)=\ln{x}+\ln{y}???
The general log rule and product rule for natural logs
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
How to add natural logs
Example
Simplify the expression.
???\ln{64}+\ln{16}???
First, we can use the product rule.
???\ln(xy)=\ln{x}+\ln{y}???
???\ln(64 \cdot 16)???
???\ln(1,024)???
From here, we can use a calculator to find the approximate value of this natural log.
???\ln(1,024)\approx6.9315???
Or we could let ???\ln(1,024)=x???. Then
???e^x=1,024???
The way we solve equations in this form, where the variable is tucked inside the exponent of the exponential, is to take the natural logarithm of both sides.
???\ln{e^x}=\ln{1,024}???
Now note that ???\ln{(e^x)}=x???, because any exponential function ???a^x??? and the associated log function (???\log_a{x}???) are inverses of each other. So if we evaluate ???a^x???, and then take the log (to base ???a???) of the result, we get back to our starting point (???x???). This means that our equation simplifies to
???x=\ln{1,024}???
???x\approx6.9315???
Quotient rule
The quotient rule for logs is
???\log_a\left(\frac{x}{y}\right)=\log_ax-\log_ay???
In terms of natural logarithms, this same rule is
???\ln\left(\frac{x}{y}\right)=\ln{x}-\ln{y}???
As with all log rules, remember that we can use this equation in either direction. If we start with something that matches the expression from the left side of the equation, we can rewrite it like the right side of the equation, or vice versa.
Example
Write the expression as one logarithm.
???\ln{32}-\ln{8}???
Using the quotient rule for natural logs,
???\ln\left(\frac{x}{y}\right)=\ln{x}-\ln{y}???
we can rewrite the expression as one logarithm.
???\ln{\frac{32}{8}}???
???\ln{4}???
We can leave the logarithm this way, as an exact value, or we can use a calculator to find an approximate value.
???\ln{4}\approx1.3863???
The power rule
The power rule for logs is
???\log_a{(x^n)}=n\log_ax???
And the same rule applies to natural logs.
???\ln{(x^n)}=n\ln{x}???
Let’s do an example.
Example
Write the expression as one logarithm.
???\ln{(8^4)}-\ln{(8^2)}???
There are multiple ways to approach this problem, but let’s start by using power rule.
???\ln{(8^4)}-\ln{(8^2)}???
???4\ln{8}-2\ln{8}???
???2\ln{8}???
We can leave the logarithm in this form, or we can pull the ???2??? back in as an exponent.
???\ln{(8^2)}???
???\ln{64}???
We can also use power rule to break down a logarithm like ???\ln{64}???. For instance, we know that ???64??? is the same as ???2^6???. Therefore, one way to rewrite ???\ln{64}??? is as
???\ln{(2^6)}???
???6\ln{2}???
Product, quotient, and power rules for logarithms, as well as the general rule for logs, can all be used together, in any combination, in order to solve problems with natural logs.
Combining natural log rules
Product, quotient, and power rules for logarithms, as well as the general rule for logs, can all be used together, in any combination, in order to solve problems with natural logs.
Special values for natural logs
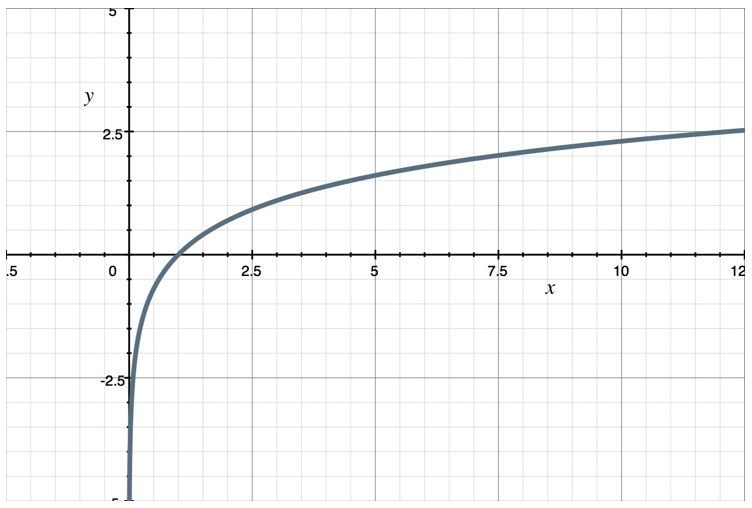
We’ll look at graphs of exponential and logarithmic functions in the next couple of lessons, but for now, let’s take a sneak peak at the graph of the natural log function, ???\ln{x}???:
Notice how the graph dips down sharply as it approaches ???x=0??? from the right side (as positive values of ???x??? get closer and closer to ???0???). This shows that the value of the natural log function goes to ???-\infty??? as ???x\to0??? from the right side, and that the natural log function is undefined at ???x=0???.
Also, as you’ve already learned, the natural log function is undefined at all ???x<0???. As ???x\to\infty???, the value of the natural log function increases without bound. And the graph of the natural log function crosses the ???x???-axis at ???x=1???, which means that ???\ln{1}=0???. To see this algebraically, we could set ???\ln{x}??? equal to ???0??? (write the equation ???\ln{x}=0???) and then solve for ???x???. In exponential form, this equation is ???e^0=x???. Since ???e^0=1???, we get ???1=x???.
So based on its graph, we can say that there are a few key values for the natural log:
???\ln{0}=\text{undefined}???
???\ln{1}=0???
???\ln{\infty}=\infty???