The Cartesian coordinate system, and graphing points
What is the Cartesian coordinate system?
The Cartesian coordinate system is the structure we use to graph points in two dimensions.
Something that has two dimensions is a surface. The Cartesian coordinate system (also called the Cartesian plane, or just “the plane”) is a flat surface (like the cover of a book) that extends forever in all directions.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
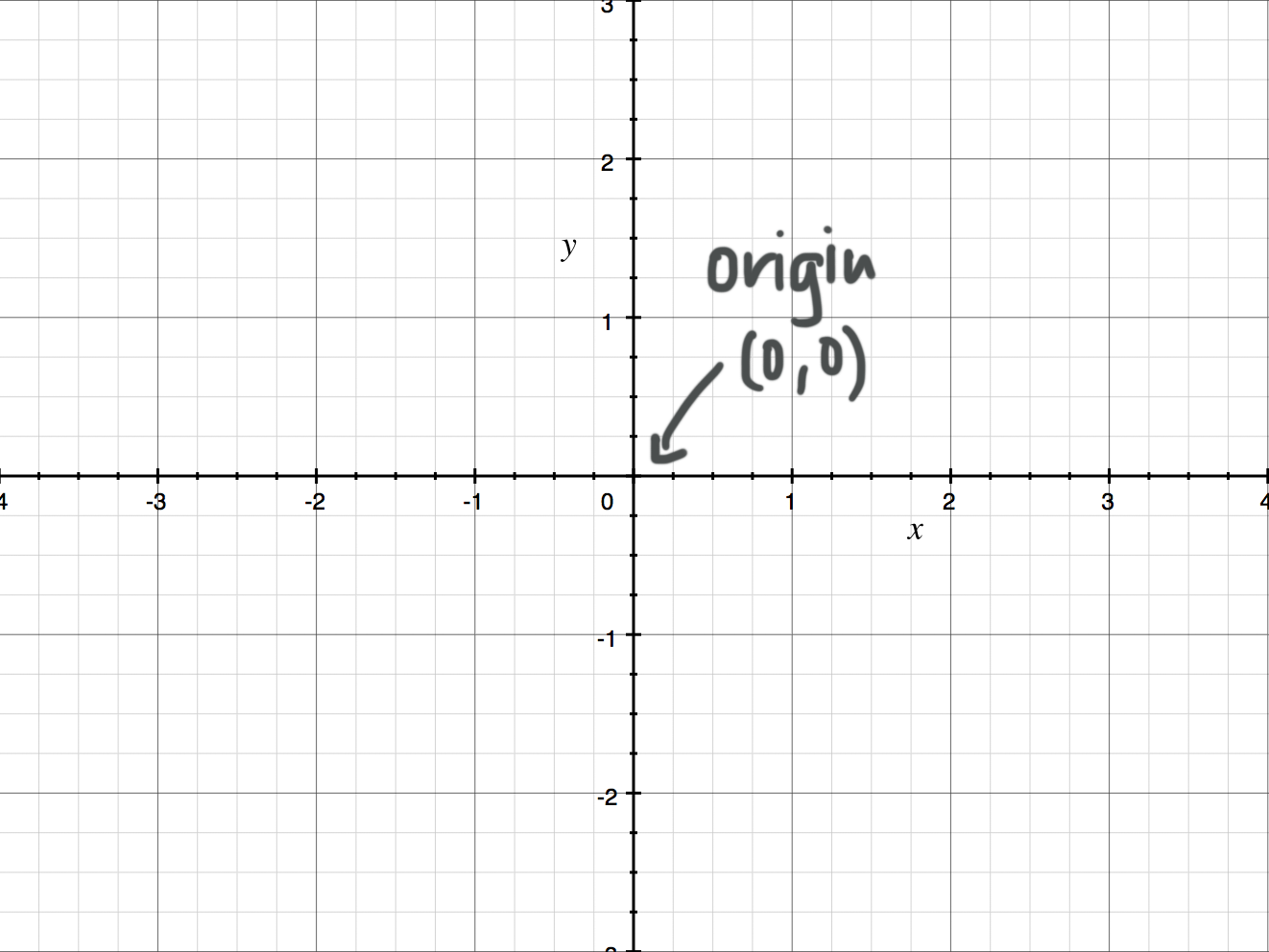
It’s made up of a pair of perpendicular lines - one horizontal and the other vertical - called axes, and the point where they meet, called the origin.
We call the horizontal axis the ???x???-axis, and the vertical axis the ???y???-axis. We sometimes refer to them, together, as the coordinate axes. We draw arrows at the ends of the axes to indicate that they extend forever. Also, we call the part of the ???x???-axis that’s to the right of the origin the positive ???x???-axis, and the part that’s to the left of the origin the negative ???x???-axis.
Similarly, we call the part of the ???y???-axis that’s above the origin the positive ???y???-axis, and the part that’s below the origin the negative ???y???-axis.
We represent every point in the plane by a pair of numbers ???(x,y)???, called its coordinates, where ???x??? (called the horizontal coordinate or the ???x???-coordinate) is the horizontal (left-right) location of the point (think “???x??? marks the spot on the ground” to help you remember), and ???y??? (called the vertical coordinate or the ???y???-coordinate) is the vertical (up-down) location of the point (think “???y??? to the sky”). A pair ???(x,y)??? is actually called an ordered pair, because the order of the numbers ???x??? and ???y??? matters. The first number in the ordered pair is the ???x???-coordinate, and the second number is the ???y???-coordinate.
The ???x???-coordinate of a point in the plane is positive if the point is located to the right of the ???y???-axis, negative if it’s located to the left of the ???y???-axis, and ???0??? if it’s located on the ???y???-axis. Similarly, the ???y???-coordinate of a point is positive if the point is located above the ???x???-axis, negative if it’s located below the ???x???-axis, and ???0??? if it’s located on the ???x???-axis. The origin is the center of the coordinate system, so its coordinates are ???(0,0)???. In other words, its ???x???-coordinate is ???0??? and its ???y???-coordinate is ???0???.
The axes divide the coordinate plane into four parts, called quadrants. Quadrant I is where ???x??? and ???y??? are both positive. The other three quadrants are named in order going counterclockwise.
Quadrant I: both ???x??? and ???y??? are positive ???(+,+)???
Quadrant II: ???x??? is negative and ???y??? is positive ???(-,+)???
Quadrant III: both ???x??? and ???y??? are negative ???(-,-)???
Quadrant IV: ???x??? is positive and ???y??? is negative ???(+,-)???
Quadrants I, II, III, and IV are also called the first, second, third, and fourth quadrants, respectively.
We “graph a point” in the plane by placing a dot at its location in the Cartesian coordinate system. We sometimes say that we “plot a point,” which means the same thing.
How to graph points in the Cartesian coordinate system
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Heading
Example
Graph the point in the Cartesian coordinate system.
???(2,5)???
Remember that points are in the form ???(x,y)???, so the ???2??? tells us how to move on the ???x???-axis (left or right) and the ???5??? tells us how to move on the ???y???-axis (up or down). Since the ???x???-coordinate (???2???) is positive, we move ???2??? units from the origin in the direction of the positive ???x???-axis (to the right). And since the ???y???-coordinate (???5???) is positive, we move ???5??? units up from there in the direction of the positive ???y???-axis (up).
Let’s try another example of graphing in the Cartesian coordinate system.
We “graph a point” in the plane by placing a dot at its location in the Cartesian coordinate system.
Example
In which quadrant would you plot the point?
???(1,-7)???
Since the ???x???-coordinate is positive and the ???y???-coordinate is negative, the correct quadrant is Quadrant IV.