How to find eigenvalues, eigenvectors, and eigenspaces

What are eigenvectors and eigenvalues?

Any vector $\vec{v}$ that satisfies $T(\vec{v})=\lambda\vec{v}$ is an eigenvector for the transformation $T$, and $\lambda$ is the eigenvalue that’s associated with the eigenvector $\vec{v}$. The transformation $T$ is a linear transformation that can also be represented as $T(\vec{v})=A\vec{v}$.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

The first thing you want to notice about $T(\vec{v})=\lambda\vec{v}$, is that, because $\lambda$ is a constant that acts like a scalar on $\vec{v}$, we’re saying that the transformation of $\vec{v}$, $T(\vec{v})$, is really just a scaled version of $\vec{v}$.

We could also say that the eigenvectors $\vec{v}$ are the vectors that don’t change direction when we apply the transformation matrix $T$. So if we apply $T$ to a vector $\vec{v}$, and the result $T(\vec{v})$ is parallel to the original $\vec{v}$, then $\vec{v}$ is an eigenvector.

Identifying eigenvectors

In other words, if we define a specific transformation $T$ that maps vectors from $\mathbb{R}^n$ to $\mathbb{R}^n$, then there may be certain vectors in the domain that change direction under the transformation $T$. For instance, maybe the transformation $T$ rotates vectors by $30^\circ$. Vectors that rotate by $30^\circ$ will never satisfy $T(\vec{v})=\lambda\vec{v}$.

But there may be other vectors in the domain that stay along the same line under the transformation, and might just get scaled up or scaled down by $T$. Those are the vectors that will satisfy $T(\vec{v})=\lambda\vec{v}$, which means that those are the eigenvectors for $T$. And this makes sense, because $T(\vec{v})=\lambda\vec{v}$ literally reads “the transformed version of $\vec{v}$ is the same as the original $\vec{v}$, but just scaled up or down by $\lambda$.”

The way to really identify an eigenvector is to compare the span of $\vec{v}$ with the span of $T(\vec{v})$. The span of any single vector $\vec{v}$ will always be a line. If, under the transformation $T$, the span remains the same, such that $T(\vec{v})$ has the same span as $\vec{v}$, then you know $\vec{v}$ is an eigenvector. The vectors $\vec{v}$ and $T(\vec{v})$ might be different lengths, but their spans are the same because they lie along the same line.

The reason we care about identifying eigenvectors is because they often make good basis vectors for the subspace, and we’re always interested in finding a simple, easy-to-work-with basis.

Finding eigenvalues

Because we’ve said that $T(\vec{v})=\lambda\vec{v}$ and $T(\vec{v})=A\vec{v}$, it has to be true that $A\vec{v}=\lambda\vec{v}$. Which means eigenvectors are any vectors $\vec{v}$ that satisfy $A\vec{v}=\lambda\vec{v}$.

We also know that there will be $2$ eigenvectors when $A$ is $2\times2$, that there will be $3$ eigenvectors when $A$ is $3\times3$, and that there will be $n$ eigenvectors when $A$ is $n\times n$.

While $\vec{v}=\vec{O}$ would satisfy $A\vec{v}=\lambda\vec{v}$, we don’t really include that as an eigenvector. The reason is first, because it doesn’t really give us any interesting information, and second, because $\vec{v}=\vec{O}$ doesn’t allow us to determine the associated eigenvalue $\lambda$.

So we’re really only interested in the vectors $\vec{v}$ that are nonzero. If we rework $A\vec{v}=\lambda\vec{v}$, we could write it as

$\vec{O}=\lambda\vec{v}-A\vec{v}$

$\vec{O}=\lambda I_n\vec{v}-A\vec{v}$

$(\lambda I_n-A)\vec{v}=\vec{O}$

Realize that this is just a matrix-vector product, set equal to the zero vector. Because $\lambda I_n-A$ is just a matrix. The eigenvalue $\lambda$ acts as a scalar on the identity matrix $I_n$, which means $\lambda I_n$ will be a matrix. If, from $\lambda I_n$, we subtract the matrix $A$, we’ll still just get another matrix, which is why $\lambda I_n-A$ is a matrix. So let’s make a substitution $B=\lambda I_n-A$.

$B\vec{v}=\vec{O}$

Written this way, we can see that any vector $\vec{v}$ that satisfies $B\vec{v}=\vec{O}$ will be in the null space of $B$, $N(B)$. But we already said that $\vec{v}$ was going to be nonzero, which tells us right away that there must be at least one vector in the null space that’s not the zero vector. Whenever we know that there’s a vector in the null space other than the zero vector, we conclude that the matrix $B$ (the matrix $\lambda I_n-A$) has linearly dependent columns, and that $B$ is not invertible, and that the determinant of $B$ is $0$, $|B|=0$.

Which means we could come up with these rules:

$A\vec{v}=\lambda\vec{v}$ for nonzero vectors $\vec{v}$ if and only if $|\lambda I_n-A|=0$.

$\lambda$ is an eigenvalue of $A$ if and only if $|\lambda I_n-A|=0$.

With these rules in mind, we have everything we need to find the eigenvalues for a particular matrix.

How to find eigenvalues, eigenvectors, and eigenspaces

---

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

---

Finding the eigenvalues of the transformation

Example

Find the eigenvalues of the transformation matrix $A$.

We need to find the determinant $|\lambda I_n-A|$.

Then the determinant of this resulting matrix is

$(\lambda-2)(\lambda-2)-(-1)(-1)$

$(\lambda-2)(\lambda-2)-1$

$\lambda^2-4\lambda+4-1$

$\lambda^2-4\lambda+3$

This polynomial is called the characteristic polynomial. Remember that we’re trying to satisfy $|\lambda I_n-A|=0$, so we can set this characteristic polynomial equal to $0$, and get the characteristic equation:

$\lambda^2-4\lambda+3=0$

To solve for $\lambda$, we’ll always try factoring, but if the polynomial can’t be factored, we can either complete the square or use the quadratic formula. This one can be factored.

$(\lambda-3)(\lambda-1)=0$

$\lambda=1$ or $\lambda=3$

So assuming non-zero eigenvectors, we’re saying that $A\vec{v}=\lambda\vec{v}$ can be solved for $\lambda=1$ and $\lambda=3$.

---

The reason we care about identifying eigenvectors is because they often make good basis vectors for the subspace, and we’re always interested in finding a simple, easy-to-work-with basis.

We want to make a couple of important points, which are both illustrated by this last example.

First, the sum of the eigenvalues will always equal the sum of the matrix entries that run down its diagonal. In the matrix $A$ from the example, the values down the diagonal were $2$ and $2$. Their sum is $4$, which means the sum of the eigenvalues will be $4$ as well. The sum of the entries along the diagonal is called the trace of the matrix, so we can say that the trace will always be equal to the sum of the eigenvalues.

$\text{Trace}(A)=\text{sum of }A\text{'s eigenvalues}$

Realize that this also means that, for an $n\times n$ matrix $A$, once we find $n-1$ of the eigenvalues, we’ll already have the value of the $n$th eigenvalue.

Second, the determinant of $A$, $|A|$, will always be equal to the product of the eigenvalues. In the last example, $|A|=(2)(2)-(1)(1)=4-1=3$, and the product of the eigenvalues was $\lambda_1\lambda_2=(1)(3)=3$.

$\text{Det}(A)=|A|=\text{product of }A\text{'s eigenvalues}$

Finding eigenvectors

Once we’ve found the eigenvalues for the transformation matrix, we need to find their associated eigenvectors. To do that, we’ll start by defining an eigenspace for each eigenvalue of the matrix.

The eigenspace $E_\lambda$ for a specific eigenvalue $\lambda$ is the set of all the eigenvectors $\vec{v}$ that satisfy $A\vec{v}=\lambda\vec{v}$ for that particular eigenvalue $\lambda$.

As we know, we were able to rewrite $A\vec{v}=\lambda\vec{v}$ as $(\lambda I_n-A)\vec{v}=\vec{O}$, and we recognized that $\lambda I_n-A$ is just a matrix. So the eigenspace is simply the null space of the matrix $\lambda I_n-A$.

$E_\lambda=N(\lambda I_n-A)$

To find the matrix $\lambda I_n-A$, we can simply plug the eigenvalue into the value we found earlier for $\lambda I_n-A$. Let’s continue on with the previous example and find the eigenvectors associated with $\lambda=1$ and $\lambda=3$.

---

Example

For the transformation matrix $A$, we found eigenvalues $\lambda=1$ and $\lambda=3$. Find the eigenvectors associated with each eigenvalue.

With $\lambda=1$ and $\lambda=3$, we’ll have two eigenspaces, given by $E_\lambda=N(\lambda I_n-A)$. With

we get

and

Therefore, the eigenvectors in the eigenspace $E_1$ will satisfy

$v_1+v_2=0$

$v_1=-v_2$

So with $v_1=-v_2$, we’ll substitute $v_2=t$, and say that

$\begin{bmatrix}v_1\\ v_2\end{bmatrix}=t\begin{bmatrix}-1\\ 1\end{bmatrix}$

Which means that $E_1$ is defined by

$E_1=\text{Span}\Big(\begin{bmatrix}-1\\ 1\end{bmatrix}\Big)$

And the eigenvectors in the eigenspace $E_3$ will satisfy

$v_1-v_2=0$

$v_1=v_2$

And with $v_1=v_2$, we’ll substitute $v_2=t$, and say that

$\begin{bmatrix}v_1\\ v_2\end{bmatrix}=t\begin{bmatrix}1\\ 1\end{bmatrix}$

Which means that $E_3$ is defined by

$E_3=\text{Span}\Big(\begin{bmatrix}1\\ 1\end{bmatrix}\Big)$

---

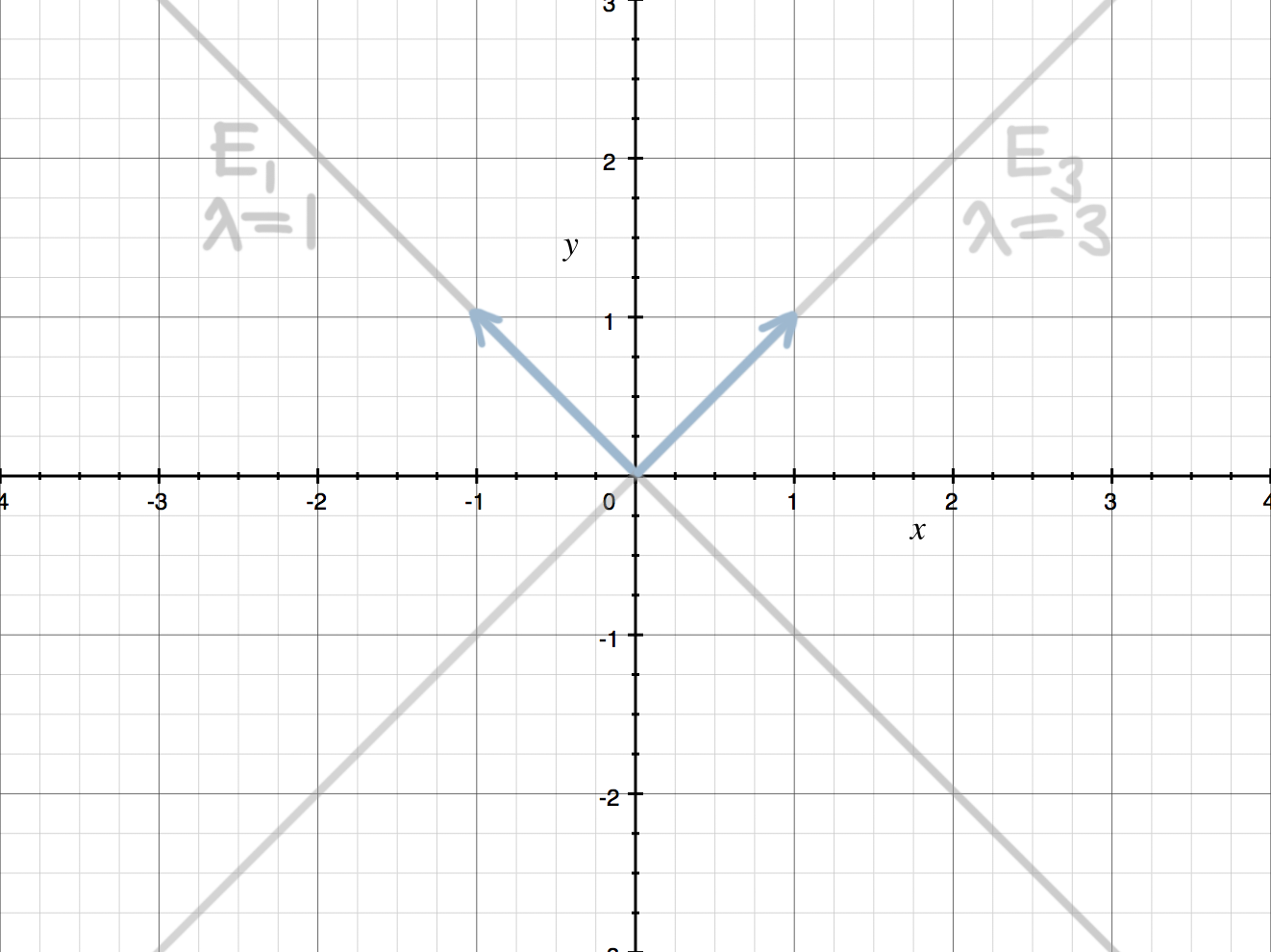
If we put these last two examples together (the first one where we found the eigenvalues, and this second one where we found the associated eigenvectors), we can sketch a picture of the solution. For the eigenvalue $\lambda=1$, we got

$E_1=\text{Span}\Big(\begin{bmatrix}-1\\ 1\end{bmatrix}\Big)$

We can sketch the spanning eigenvector $\vec{v}=(-1,1)$,

and then say that the eigenspace for $\lambda=1$ is the set of all the vectors that lie along the line created by $\vec{v}=(-1,1)$.

Then for the eigenvalue $\lambda=3$, we got

$E_3=\text{Span}\Big(\begin{bmatrix}1\\ 1\end{bmatrix}\Big)$

We can add to our sketch the spanning eigenvector $\vec{v}=(1,1)$,

and then say that the eigenspace for $\lambda=3$ is the set of all the vectors that lie along the line created by $\vec{v}=(1,1)$.

In other words, we know that, for any vector $\vec{v}$ along either of these lines, when you apply the transformation $T$ to the vector $\vec{v}$, $T(\vec{v})$ will be a vector along the same line, it might just be scaled up or scaled down.

Specifically,

• since $\lambda=1$ in the eigenspace $E_1$, any vector $\vec{v}$ in $E_1$, under the transformation $T$, will be scaled by $1$, meaning that $T(\vec{v})=\lambda\vec{v}=1\vec{v}=\vec{v}$, and

• since $\lambda=3$ in the eigenspace $E_3$, any vector $\vec{v}$ in $E_3$, under the transformation $T$, will be scaled by $3$, meaning that $T(\vec{v})=\lambda\vec{v}=3\vec{v}$.

---

Get access to the complete Linear Algebra course

---

---

---