Inverses of linear transformations
What is an inverse transformation?
Previously we talked about a transformation as a mapping, something that maps one vector to another.
So if a transformation maps vectors from the subset ???A??? to the subset ???B???, such that if ???\vec{a}??? is a vector in ???A???, the transformation will map it to a vector ???\vec{b}??? in ???B???, then we can write that transformation as ???T: A\to B???, or as ???T(\vec{a})=\vec{b}???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
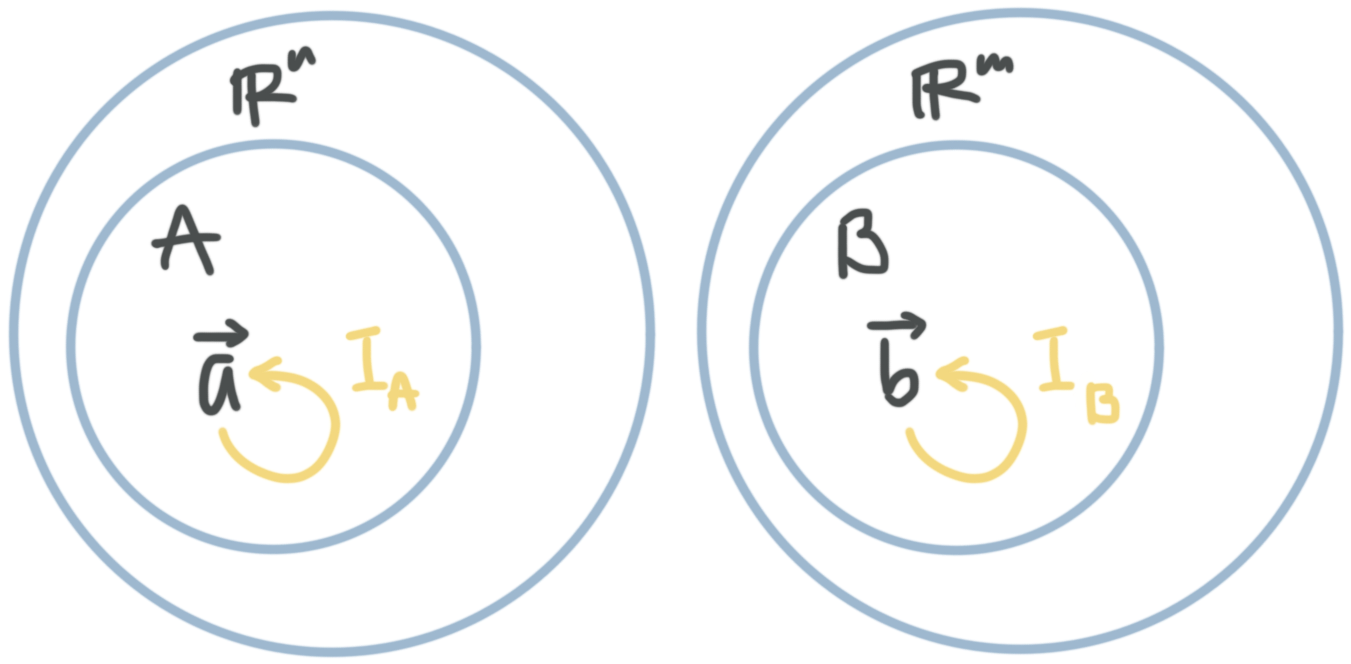
The identity transformation
With that in mind, we want to define the identity transformation as the transformation that maps vectors to themselves. There’s no trick here. The identity transformation ???I??? literally just says, given any vector ???\vec{x}??? in ???X???, the transformation will map it to ???\vec{x}???, itself. In other words, ???I: X\to X???, or as ???I_x(\vec{x})=\vec{x}???.
So for a vector ???\vec{a}??? in the subset ???A???, the identity transformation would be ???I: A\to A???, or ???I_A(\vec{a})=\vec{a}???. And for a vector ???\vec{b}??? in the subset ???B???, the identity transformation would be ???I: B\to B???, or ???I_B(\vec{b})=\vec{b}???.
Invertibility and inverse transformations
So we know that the identity transformation maps a vector to itself, without, in a way, ever really leaving the subset.
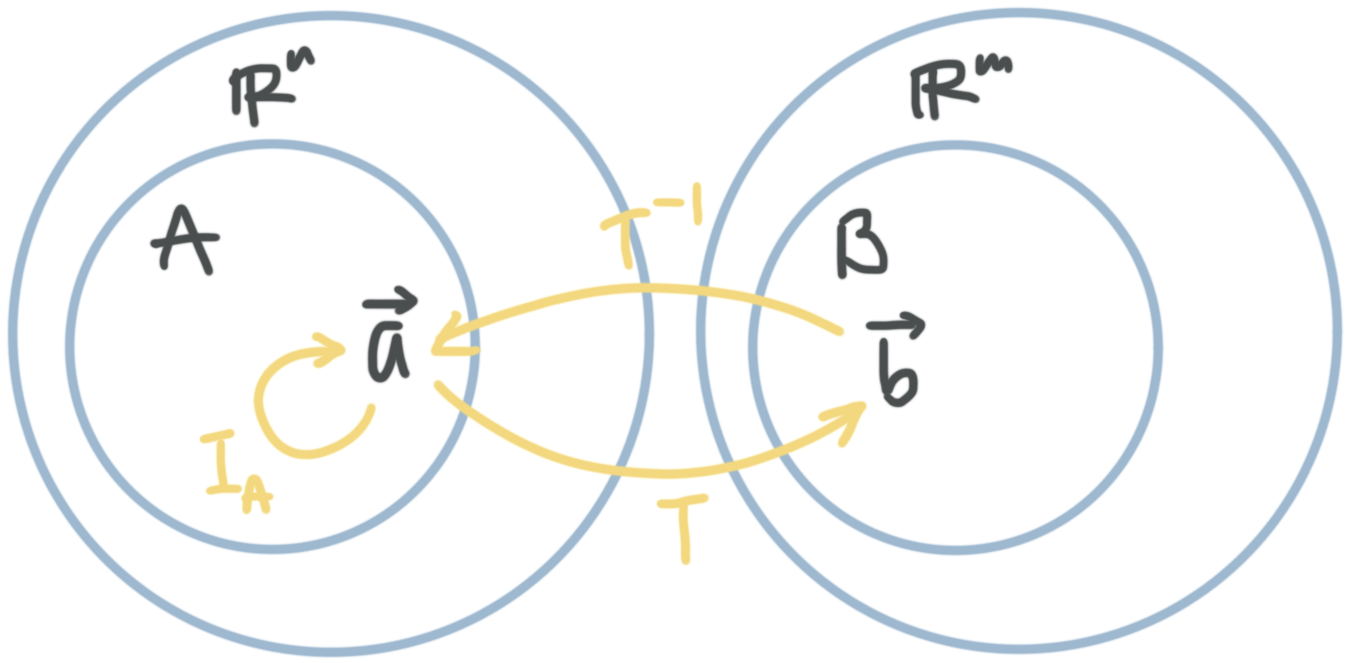
What we want to know now is whether we can use a transformation to map a vector from one subset ???A??? to another subset ???B???, and then undo the process, mapping the result we got in ???B??? back into ???A???, and end up with the same vector in ???A??? that we started with. In a sense, we’d just end up with the identity transformation, but we would have left the subset and come back again.
If we can do this for every vector ???\vec{a}??? in ???A??? (use a transformation to map ???\vec{a}??? in ???A??? to ???\vec{b}??? in ???B???, and then reverse the process to map ???\vec{b}??? back to the ???\vec{a}??? we started with), then the transformation is invertible.
In other words, a transformation is invertible if it has an inverse. If ???T: A\to B???, then ???T??? is invertible if and only if its inverse ???T^{-1}: B\to A??? exists, such that the composition of ???T??? with ???T^{-1}??? and vice versa are both defined by the identity transformations we talked about earlier:
???T^{-1}\circ T=I_A???
???T\circ T^{-1}=I_B???
This make sense. If ???T: A\to B??? and ???T^{-1}: B\to A???, then ???T^{-1}\circ T=I_A??? could be written as
???T^{-1}\circ T=I_A???
???T^{-1}(T(\vec{a}))=I_A(\vec{a})???
The transformation ???T(\vec{a})??? maps a vector ???\vec{a}??? in ???A??? to some ???\vec{b}??? in ???B???. But then ???T^{-1}??? takes that result ???\vec{b}??? in ???B??? and maps that vector back to an ???\vec{a}??? in ???A???. In other words, we started at a vector ???\vec{a}??? in ???A???, and ended up right back at the exact same vector ???\vec{a}??? in ???A???, which we know now is just the identity transformation for ???A???, ???I_A???. And we could follow the opposite logical path for ???T\circ T^{-1}=I_B???.
And of course, if ???T??? and ???T^{-1}??? are inverses of one another, it’s implied that the domain of ???T??? is the codomain of ???T^{-1}???, and that the domain of ???T^{-1}??? is the codomain of ???T???.
Invertibility and uniqueness
If a transformation is invertible, there are really three other related conclusions we can make.
1. Its inverse transformation is unique. In other words, an invertible transformation cannot have multiple inverses. It will always have exactly one inverse.
2. When you apply the transformation ???T??? to a vector ???\vec{a}??? in ???A???, you’ll be mapped to one unique vector ???\vec{b}??? in ???B???. In other words, the transformation can never map you from ???\vec{a}??? in ???A??? to multiple values ???\vec{b}_1??? and ???\vec{b}_2??? in ???B???.
3. When you apply the inverse transformation ???T^{-1}??? to a vector ???\vec{b}??? in ???B???, you’ll be mapped back to one unique vector ???\vec{a}??? in ???A???. In other words, the unique inverse transformation can never map you from ???\vec{b}??? in ???B??? back to multiple vectors ???\vec{a}_1??? and ???\vec{a}_2??? in ???A???.
Surjective and injective
If ???T??? is a transformation that maps vectors in the subset ???A??? to vectors in the subset ???B???, ???T:A\to B???, and if every vector ???\vec{b}??? in ???B??? is being mapped to at least once by some vector(s) ???\vec{a}??? in ???A??? such that ???T(\vec{a})=\vec{b}???, then ???T??? is a surjective transformation, also called an onto transformation. If there’s any vector ???\vec{b}??? in ???B??? which, via ???T???, is not mapped to by any ???\vec{a}??? in ???A???, then ???T??? is not surjective; it’s not onto.
If every vector ???\vec{b}??? in ???B??? is being mapped to, then ???T??? is surjective, or onto.
If ???T??? is a transformation that maps vectors in the subset ???A??? to vectors in the subset ???B???, ???T:A\to B???, and if every vector ???\vec{b}??? in ???B??? is being mapped to by at most one vector ???\vec{a}??? in ???A??? such that ???T(\vec{a})=\vec{b}???, then ???T??? is an injective transformation, also called a one-to-one transformation. If there is any vector ???\vec{b}??? in ???B??? which, via ???T???, is mapped to by two or more ???\vec{a}??? in ???A???, then ???T??? is not injective; it’s not one-to-one.
If every ???\vec{a}??? maps to a unique ???\vec{b}???, then ???T??? is injective, or one-to-one.
In other words, if there’s a vector ???\vec{b}??? in ???B??? that’s not being mapped to, then the transformation isn’t surjective. But if there are multiple vectors ???\vec{a}_1??? and ???\vec{a}_2??? in ???A??? being mapped to the same vector ???\vec{b}??? in ???B???, then the transformation isn’t injective.
And remember before that we said a transformation was invertible if we could find an inverse transformation, and we know that a transformation will only ever have one inverse.
If we formalize that definition, we’re saying that:
A transformation is invertible if, for every ???\vec{b}??? in ???B???, there’s a unique ???\vec{a}??? in ???A???, such that ???T(\vec{a})=\vec{b}???.
This definition is telling us that every ???\vec{b}??? is being mapped to, which means the transformation is surjective, or onto. The definition is also telling us that there’s a unique ???\vec{a}??? in ???A??? that’s mapping to each ???\vec{b}???, which means the transformation is injective, or one-to-one.
Therefore, we can say that a transformation ???T??? is invertible if and only if ???T??? is both surjective and injective.
How to find the inverse of a transformation
Take the course
Want to learn more about Linear Algebra? I have a step-by-step course for that. :)
Say whether the transformation is invertible, given information about specific vectors in set A that map to specific vectors in set B
Example
Say whether the transformation ???T??? is invertible.
In order for the transformation to be invertible, it must be both surjective and injective (onto and one-to-one).
If we look at the picture of the transformation, we can see that every ???\vec{b}??? in ???B??? is being mapped to by an ???\vec{a}??? in ???A???, which means the transformation is surjective.
In other words, a transformation is invertible if it has an inverse.
But we can see that both ???\vec{a}_2??? and ???\vec{a}_3??? are mapping to ???\vec{b}_3???, which means we have multiple ???\vec{a}???’s in ???A??? mapping to the same ???\vec{b}??? in ???B???, and therefore that the transformation is not injective.
The transformation is invertible if and only if it’s both surjective and injective. In this example, it’s surjective, but not injective, and therefore, it’s not invertible. The transformation does not have an inverse.