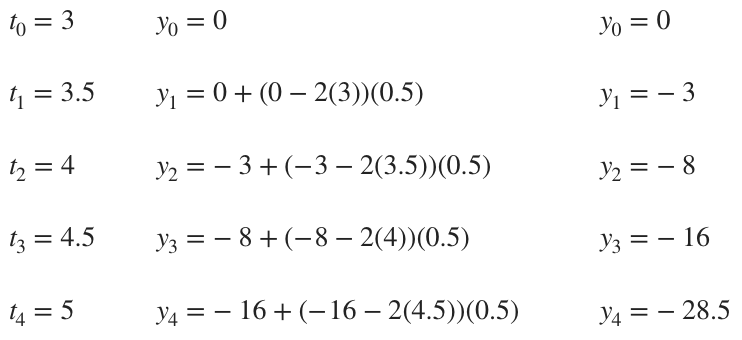Euler's method for solving differential equations

Euler’s method approximates the solution to a differential equation

Euler’s Method helps you approximate solutions to differential equations.

You’ll always be given an equation and an initial condition, and you’ll use this information to carry out the Euler’s approximation in multiple steps.

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

The better approximation you want, the more steps you have to take. The only formula you’ll need to remember is

$y_1=y_0+[f(t_0,y_0)]\Delta t$

In this formula, $y_1$ represents the first $y$ value you’ll need to calculate. $y_0$ and $t_0$ are the values you’re given in the initial condition, and $\Delta t$ is the distance between values of $t$ .

Note that the values of $t$ and $y$ given in the initial condition are denoted by $t_0$ and $y_0$ . This does not necessarily mean that $t=0$ or that $y=0$ . This only means that these values of $t$ and $y$ were given in the original problem.

Each subsequent approximation of $y$ is denoted by $y_1$ , $y_2$ , $y_3$ , ... $y_n$ and each value of $t$ for which $y$ is estimated is denoted by $t_1$ , $t_2$ , $t_3$ , ... $t_n$ . The “step-size” or the distance between two successive values of $t$ at which $y$ is approximated is often denoted by $h$ or $\Delta{t}$ .

Making a table to approximate the solution in steps

Take the course

Want to learn more about Differential Equations? I have a step-by-step course for that. :)

Learn More

Using Euler’s method with two steps to find the solution to the differential equation

Example

Use Euler’s Method and two steps, find $y(1)$ if $y'=y-t$ and $y(0)=2$ .

To find step size, divide the change in $t$ (from $0$ to $1$ ; $y(0)$ to $y(1)$ ) by the number of steps, in our case, two.

$\frac{1-0}{2}=\frac12=0.5=\Delta t$

Now we can start building our table. $t_0$ and $y_0$ both come from our initial condition, $y(0)=2$ . To find $t_1$ and $t_2$ , we add $\Delta t$ to the previous value for $t$ . We do that until we reach $t_n=1$ , which is the value the problem originally asked for when it asked us to find $y(1)$ .

We find $y_1$ and $y_2$ using the Euler’s Method equation mentioned at the beginning of this section. To calculate $y_1$ , we plug in the values of $t_0$ and $y_0$ . To calculate $y_2$ , we plug in the values of $t_1$ and $y_1$ , and so on. In other words, looking at the table above, use the values from the row above the value you’re trying to calculate.

$y(1)=4.25$

We’ll look at one more example of a problem worded slightly differently.

One thing you MUST remember whenever you’re using Euler’s Method, is to keep ALL of your decimal places until you get to the last value of $y$ , and you’ve found your final answer. Remember that Euler’s Method is about approximation, so if you start rounding off decimal places prior to the end of the problem, your approximation will get less and less accurate as you go. Therefore, if your calculator gives you twelve decimal places, write down every single one until you get your final answer. THEN, and ONLY then, can you round your answer.

Euler's method for Differential Equations.jpg — One thing you MUST remember whenever you’re using Euler’s Method, is to keep ALL of your decimal places until you get to the last value of Y.

Example

Use Euler’s Method with step size $0.5$ to approximate the values $y_1$ , $y_2$ , $y_3$ and $y_4$ of $y'=y-2t$ when $y(3)=0$ .

Since we’re given step-size directly, we already know that

$\Delta t=0.5$

To start building our table, we first plug in $t_0$ and $y_0$ from our initial condition, $y(3)=0$ . Since we’re calculating all the way to $y_4$ , we start adding $\Delta t=0.5$ to $t_0$ until we reach $t_4$ .

Once we’ve built out the first column, we start to calculate $y_1$ using the Euler’s Method equation mentioned at the beginning of this section. To calculate $y_1$ , we’ll plug in the values of $t_0$ and $y_0$ . To calculate $y_2$ , we plug in the values of $t_1$ and $y_1$ , and so on. In other words, looking at the table above, use the values from the row above the $y$ -value you’re trying to calculate. We continue this method until we’ve found all values of $y$ through $y_4$ .