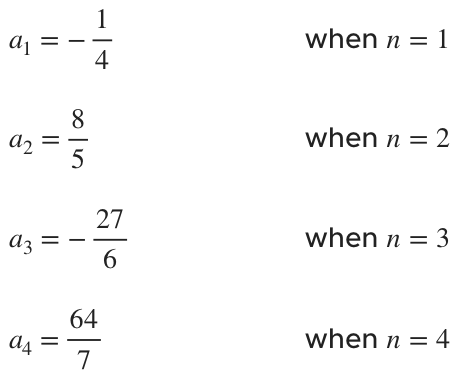How to find the formula for the general term of a sequence
What is the general term of the sequence?
The general term of a sequence ???a_n??? is a term that can represent every other term in the sequence.
It relates each term is the sequence to its place in the sequence.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
For example, given the sequence
???\{-1,-2,-3,-4,-5,\ ...\}???
we need to realize that
the first term of the sequence is ???-1???
the second term of the sequence is ???-2???
the third term of the sequence is ???-3???
the fourth term of the sequence is ???-4???
the fifth term of the sequence is ???-5???
In other words
when ???n=1???, the value of the sequence is ???-1???
when ???n=2???, the value of the sequence is ???-2???
when ???n=3???, the value of the sequence is ???-3???
when ???n=4???, the value of the sequence is ???-4???
when ???n=5???, the value of the sequence is ???-5???
Based on this information, the value of the sequence is always ???-n???, so a formula for the general term of the sequence is
???a_n=-n???
This was an easy example, but we’ll always follow this same process to find the general term of any sequence. We’ll
Match the terms of the sequence to their place in the sequence ???n???
Find the pattern that relates each term to its corresponding value of ???n???
We always have to pay special attention to the signs of the terms in the sequence.
If all of the terms in the sequence are positive, ???a_n??? will be positive.
If all of the terms in the sequence are negative, ???a_n??? will be negative (???-a_n???).
If the signs of the terms are alternating, and
if the odd terms (???n=1,\ 3,\ 5,\ ...???) are negative, ???a_n??? will include ???(-1)^n???
if the even terms (???n=2,\ 4,\ 6,\ ...???) are negative, ???a_n??? will include ???(-1)^{n-1}??? or ???(-1)^{n+1}???
How to find the general term for a sequence by relating the pattern in the terms to the corresponding value of n
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Breaking down the numerator and denominator separately to find the general term
Example
Find a formula for the general term ???a_n??? of the sequence.
???\left\{-\frac{1}{4},\frac{8}{5},-\frac{27}{6},\frac{64}{7}\right\}???
Our first step is to match the terms of the sequence to their place in the sequence ???n???. We have
Now we can start examining the sequence. First we notice that the signs of the terms are alternating, and the odd terms are negative, which means that our formula for ???a_n??? will include ???(-1)^n???.
Next, we’ll look at just the numerator of each term in our sequence. Taking the numerator only, we see that
We should recognize that these are perfect cubes. In other words
This tells us that the numerator of every term in our sequence can be represented by ???n^3???, so the numerator in the general term ???a_n??? will be ???n^3???.
The general term of a sequence a_n is a term that can represent every other term in the sequence.
It relates each term is the sequence to its place in the sequence.
Now let’s look at the denominator of each term in our sequence. Taking the denominator only, we see that
The denominator of each term is always ???3??? higher than the corresponding value of ???n???, which means that the denominator of every term in our sequence can be represented by ???n+3???, so the denominator of the general term ???a_n??? will be ???n+3???.
We’ve looked at every part of each term (the sign, the numerator, and the denominator), so it’s time to start putting it all together.
We said that we had to include ???(-1)^n??? to address the negative odd terms, that the numerator was ???n^3???, and that the denominator was ???n+3???. So a formula for the general term ???a_n??? of the sequence
???\left\{-\frac{1}{4},\frac{8}{5},-\frac{27}{6},\frac{64}{7}\right\}???
is
???a_n=(-1)^n\frac{n^3}{n+3}???
Text