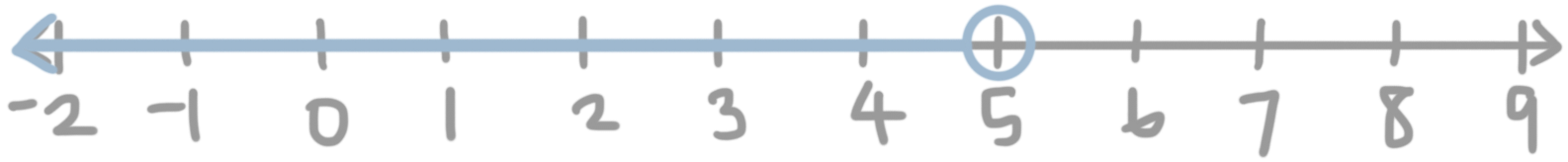How to graph inequalities on a number line
How to graph inequalities on a number line
In previous lessons we looked at how to graph points and lines in the ???xy???-plane along two axes: the horizontal ???x???-axis and the vertical ???y???-axis.
In this lesson we’re talking about graphing inequalities, which will be done on a number line.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
You can think of the number line as simply the horizontal ???x???-axis, with the vertical ???y???-axis stripped away. A number line looks like this:
It’s simply a horizontal line, extending infinitely in both directions. You’ll see negative numbers to the left of ???0??? and positive numbers to the right of ???0???. We’ll be graphing inequalities on number lines like this one.
An inequality is like an equation, but instead of an equals sign, you’ll have one of these inequality signs:
???>,\ <,\ \neq,\ \leq,\ \geq???
Before we can graph an inequality, we have to solve it. To help us in doing the graphing, we want to write the solution in a form of an inequality where only the variable is on the left side, and only a number is on the right side. That is, we want to get the solution into one of the following forms, where ???a??? is a number:
???x>a???
???x<a???
???x\neq a???
???x\leq a???
???x\geq a???
If you solve an inequality, and what you get is an inequality that has only a number on the left side, and only the variable on the right side, all you need to do is “turn the inequality around” (put the variable on the left side, and the number on the right side, and reverse the direction of the inequality sign). For example, if you solve an inequality and get ???6>x???, you can turn it around and write it as ???x<6???.
If the inequality is either ???x\geq a??? or ???x\leq a???, then (because of the “equal to” part of the inequality) the number on the right side (???a???) is part of the solution, so we draw a solid (filled-in) circle at ???a??? on our number line when we graph the inequality. If the inequality is either ???x>a??? or ???x<a???, the number on the right side (???a???) isn’t part of the solution, so we draw an open circle at ???a??? on our number line.
To graph an inequality ???x>a??? (or the “greater than” part of an inequality ???x\geq a???), we draw a ray (a line that extends infinitely in only one direction) that starts at the (solid or open) circle at ???a??? and extends infinitely to the right, since the solution of the inequality ???x>a??? consists of all numbers greater than ???a??? (all the numbers to the right of ???a??? on our number line).
Similarly, to graph an inequality ???x<a??? (or the “less than” part of an inequality ???x\leq a???), we draw a ray that starts at the (solid or open) circle at ???a??? and extends infinitely to the left, since the solution of the inequality ???x<a??? consists of all the numbers less than ???a??? (all the numbers to the left of ???a??? on our number line).
In either case, we draw an arrow to show the direction of the ray.
To summarize:
???>??? or ???\geq???: the arrow will go to the right
???<??? or ???\leq???: the arrow will go to the left
???>??? or ???<???: the circle will be open
???\geq??? or ???\leq???: the circle will be solid
If the inequality is ???x\neq a??? (“???x??? not equal to ???a???”), the solution consists of all the numbers other than ???a???. If ???a=4???, for example, the solution of the inequality ???x\le4??? consists of all the numbers other than ???4???. So we draw an open circle at ???a??? on our number line, and then we draw two rays: a ray that starts at the open circle at ???a??? and extends infinitely to the left, where we show the direction with an arrow that goes to the left, and a ray that starts at the open circle at ???a??? and extends infinitely to the right, where we show the direction with an arrow that goes to the right.
Graphing different types of inequalities on number line
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Examples of less than, and greater than or equal to inequalities on a number line
Example
Graph the inequality on a number line.
???x<5???
First draw a number line that includes the solution ???5???.
Next we’ll draw an open circle on ???5???. The circle will be open because ???x??? doesn’t equal ???5???. The arrow must extend to the left since ???x??? is less than ???5???, which means the solution is in the negative direction.
Let’s try another example of graphing inequalities.
If you solve an inequality, and what you get is an inequality that has only a number on the left side, and only the variable on the right side, all you need to do is “turn the inequality around.”
Example
Graph the inequality on a number line.
???x\geq2???
First draw a number line that includes the solution ???2???.
Next we’ll draw a closed (filled in) circle on ???2??? because ???x??? can equal ???2???. The arrow must extend to the right since ???x??? is greater than ???2???, which means the solution is in the positive direction.
