Finding infinite limits at vertical asymptotes

Infinite limits (vertical asymptotes) blog post.jpeg

Limits at infinity vs. infinite limits

There’s a difference between “limits at infinity” and “infinite limits.” When we see limits at infinity, it means we’re talking about the limit of the function as we approach $\infty$ or $-\infty$ . Contrast that with infinite limits, which means that the value of the limit is $\infty$ or $-\infty$ as we approach a particular point.

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Limits at infinity, infinite limits

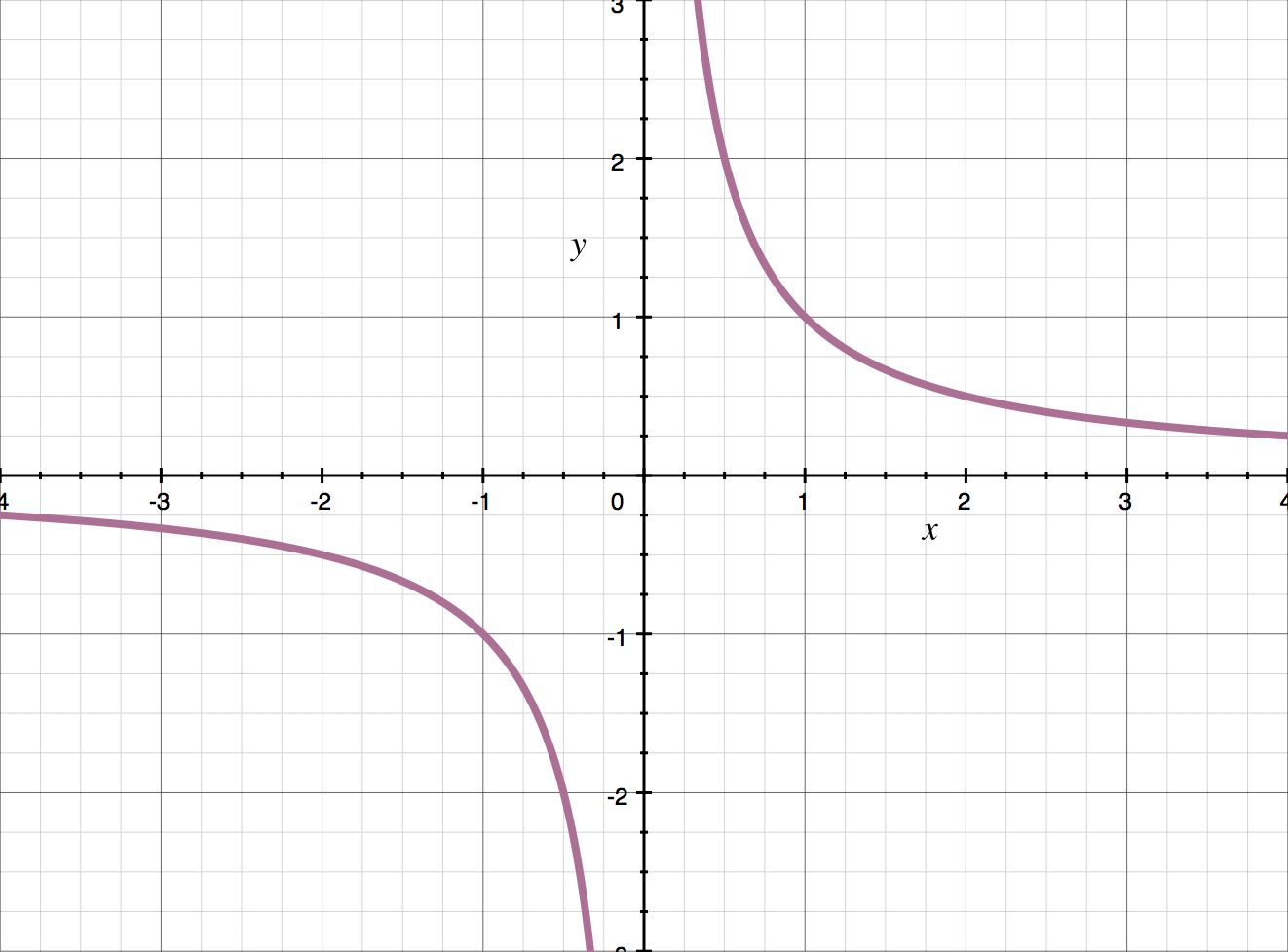
In the graph of $f(x)=1/x$ ,

the function has infinite, one-sided limits at $x=0$ . There’s a vertical asymptote there, and we can see that the function approaches $-\infty$ from the left, and $\infty$ from the right.

$\lim_{x\to0^-}\frac{1}{x}=-\infty$

$\lim_{x\to0^+}\frac{1}{x}=\infty$

Talking about limits at infinity for this function, we can see that the function approaches $0$ as we approach either $\infty$ or $-\infty$ .

$\lim_{x\to-\infty}\frac{1}{x}=0$

$\lim_{x\to\infty}\frac{1}{x}=0$

How to find infinite limits

Infinite limits exist around vertical asymptotes in the function. Of course, we get a vertical asymptote whenever the denominator of a rational function in lowest terms is equal to $0$ .

Here’s an example of a rational function in lowest terms, meaning that we can’t factor and cancel anything from the fraction.

$\lim_{x\to1}\frac{1}{(x-1)^2}$

We can see that setting $x=1$ gives $0$ in the denominator, which means that we have a vertical asymptote at $x=1$ . Therefore, we know we’ll have infinite limits on either side of $x=1$ .

Once we’ve established that this is a rational function in lowest terms and that a vertical asymptote exists, all that’s left to determine is whether the one-sided limits around $x=1$ approach $\infty$ or $-\infty$ .

In order to do that, we can substitute values very close to $x=1$ . If the result is positive, the limit will be $\infty$ ; if the result is negative, the limit will be $-\infty$ .

$f(0.99)=\frac{1}{(0.99-1)^2}=\frac{1}{(-0.01)^2}=\frac{1}{0.0001}=10,000=\infty$

$f(1.01)=\frac{1}{(1.01-1)^2}=\frac{1}{(0.01)^2}=\frac{1}{0.0001}=10,000=\infty$

Because the value of the function tends toward $\infty$ on both sides of the vertical asymptote, we can say that the general limit of the function as $x\to1$ is $\infty$ .