Intermediate value theorem

Defining the intermediate value theorem

The intermediate value theorem is a theorem we use to prove that a function has a root inside a particular interval.

The root of a function, graphically, is a point where the graph of the function crosses the $x$-axis. Algebraically, the root of a function is the point where the function’s value is equal to $0$.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Formally, the intermediate value theorem states:

Let $f(x)$ be a function which is continuous on the closed interval $[a,b]$ and let $y_0$ be a real number lying between $f(a)$ and $f(b)$. If $f(a)<y_0<f(b)$ or $f(b)<y_0<f(a)$, then there will be at least one $c$ on the interval $(a,b)$ where $y_0=f(c)$.

The formal theorem is technical, but it’s actually saying something simple, which is that, assuming $f(x)$ is continuous on $[a,b]$, if we can show that the function’s value is negative at one side of the interval and positive at the other side, then that fact alone proves that the graph of the function must cross the $x$-axis at some point inside the interval.

That being said, in order to use the intermediate value theorem, we need to 1) have a closed interval $[a,b]$ (which means that $a$ and $b$ are included as part of the interval), and 2) show that the function is continuous everywhere in the interval.

Applying the intermediate value theorem on a closed interval

---

Take the course

Want to learn more about Calculus 1? I have a step-by-step course for that. :)

---

Using the intermediate value theorem to prove the function has a root in the interval

Example

Show that the function has at least one root in the interval $[-2,5]$.

$f(x)=x^3-4x^2+7x+1$

First, we should confirm that this function is continuous over the given interval.

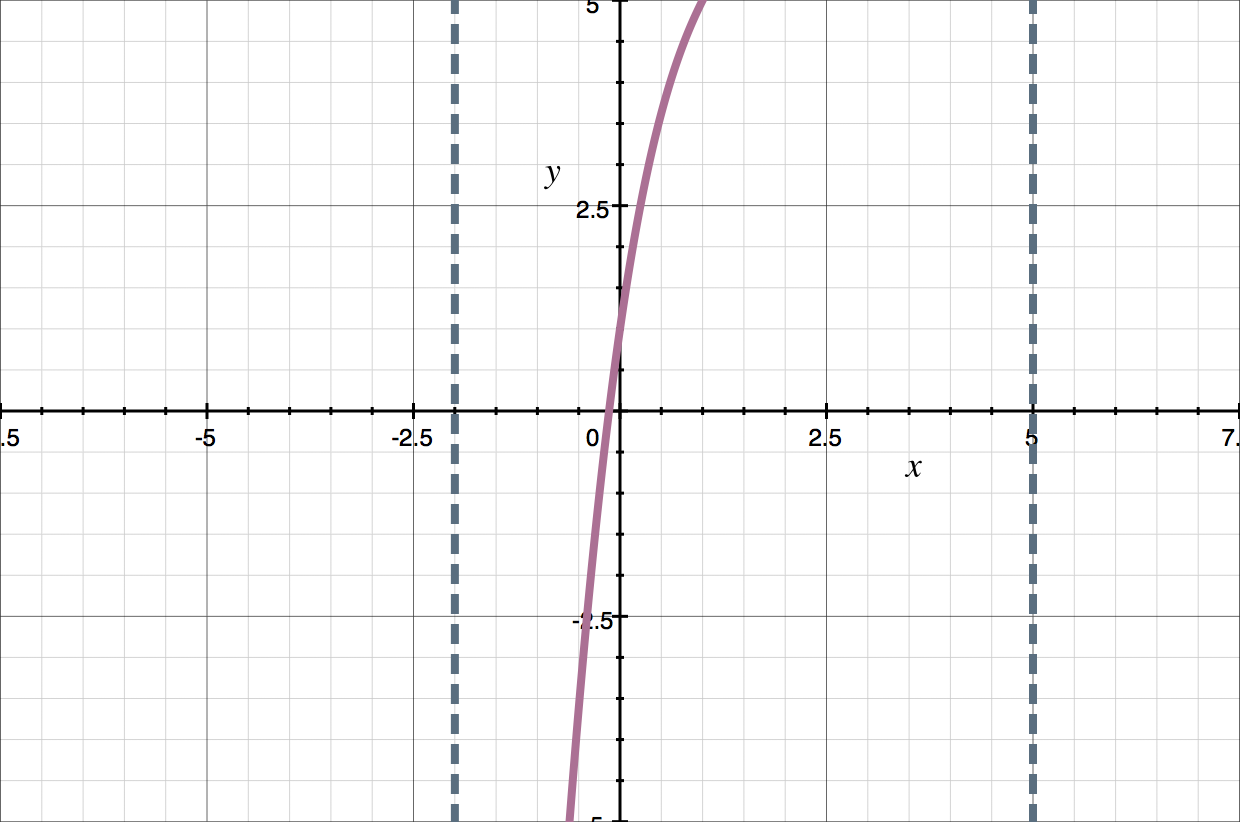
Continuity breaks typically occur in functions that have variables in the denominator of fractions, trigonometric functions, logarithmic functions, or functions with square roots. This function has none of these elements, so we know that it’s continuous. If we want to double-check ourselves, we can graph the function.

Continuity breaks typically occur in functions that have variables in the denominator of fractions, trigonometric functions, logarithmic functions, or functions with square roots.

Next we will substitute into our function using our two endpoints.

$f(-2)=(-2)^3-4(-2)^2+7(-2)+1$

$f(-2)=-8-16-14+1$

$f(-2)=-37$

and

$f(5)=(5)^3-4(5)^2+7(5)+1$

$f(5)=125-100+35+1$

$f(5)=61$

Since we know that $f(x)=x^3-4x^2+7x+1$ is continuous, and since the value of the function at the left side of the interval is negative (below the $x$-axis), and the value of the function at the right side of the interval is positive (above the $x$-axis), we know that there’s at least one point $c$ at which the function will cross the $x$-axis.

$-37<f(c)<61$

Therefore, the function has at least one solution (root) in the interval $[-2,5]$.

---

Get access to the complete Calculus 1 course

---