Linear systems in two unknowns

What is a linear system?

Throughout Linear Algebra, we’ll be really interested in solving systems of linear equations, or linear systems.

A linear system is a system of equations, defined for a set of unknown variables, where each of the variables is linear (the variables are first degree, or raised to the power of $1$ ).

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Later on we’ll learn about matrices and how to use them to solve linear systems. So in order to have a foundational understanding of what we’re doing when we solve systems, we want to take this lesson to review other basic methods for solving systems.

In an introductory Algebra class, we would have learned three ways to solve systems of linear equations: substitution, elimination, and graphing. Let’s review the steps for each of those methods.

Substitution method

Get a variable by itself in one of the equations.
Take the expression you got for the variable in step 1, and plug it (substitute it using parentheses) into the other equation.
Solve the equation in step 2 for the remaining variable.
Use the result from step 3 and plug it into the equation from step 1.

How to solve a system of two linear equations, in two unknowns

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

Learn More

There are three ways to solve a system of linear equations

Example

Find the unique solution to the system of equations.

$y=x+3$

$2x-3y=10$

Let’s solve the system using the substitution method. Since $y$ is already solved for in the first equation, step 1 is completed, and we’ll go on to step 2 by substituting $x+3$ for $y$ in the other equation.

$2x-3y=10$

$2x-3(x+3)=10$

Solve for $x$ . Start by distributing the $-3$ .

$2x-3x-9=10$

Combine like terms.

$-x-9=10$

Add $9$ to both sides.

$-x-9+9=10+9$

$-x=19$

Multiply both sides by $-1$ .

$-x(-1)=19(-1)$

$x=-19$

To find $y$ , we’ll plug in $-19$ for $x$ in the first equation.

$y=x+3$

$y=-19+3$

$y=-16$

The unique solution is $(-19,-16)$ .

We would have learned three ways to solve systems of linear equations: substitution, elimination, and graphing.

Elimination method

If necessary, rearrange both equations so that the $x$ -terms are first, followed by the $y$ -terms, the equals sign, and the constant term (in that order). If an equation appears to have not constant term, that means that the constant term is $0$ .
Multiply one (or both) equations by a constant that will allow either the $x$ -terms or the $y$ -terms to cancel when the equations are added or subtracted (when their left sides and their right sides are added separately, or when their left sides and their right sides are subtracted separately).
Add or subtract the equations.
Solve for the remaining variable.
Plug the result of step 4 into one of the original equations and solve for the other variable.

Example

Find the unique solution to the system of equations.

$y=3x-4$

$-x+2y=12$

First, we’ll rearrange the first equation so that its individual parts are in the correct places for elimination. Subtract $3x$ from both sides.

$y=3x-4$

$-3x+y=3x-3x-4$

$-3x+y=-4$

Next, multiply the result above by $2$ so that the $y$ -terms will cancel when we subtract the equations.

$2(-3x+y)=2(-4)$

$-6x+2y=-8$

Now we’ll subtract the equations.

$-6x+2y-(-x+2y)=-8-(12)$

$-6x+2y+x-2y=-8-12$

Combine like terms.

$-6x+x+2y-2y=-20$

$-5x+0=-20$

$-5x=-20$

Divide both sides by $-5$ .

$\frac{-5x}{-5}=\frac{-20}{-5}$

$x=4$

To solve for $y$ , we’ll plug in $4$ for $x$ in the original first equation.

$y=3x-4$

$y=3(4)-4$

$y=12-4$

$y=8$

The unique solution is $(4,8)$ .

Graphing method

Solve for $y$ in each equation.
Graph both equations on the same Cartesian coordinate system.
Find the point of intersection of the lines (the point where the lines cross).

Let’s look at an example using the graphing method.

Example

Graph both equations to find the solution to the system.

$x+3y=12$

$2x-y=5$

In order to graph these equations, let’s put both of them into slope-intercept form. Start with the first equation of the system. We get

$x+3y=12$

Subtract $x$ from both sides.

$x-x+3y=-x+12$

$3y=-x+12$

Divide both sides by $3$ .

$\frac{3y}{3}=-\frac{x}{3}+\frac{12}{3}$

$y=-\frac13x+4$

Now we take the second equation.

$2x-y=5$

Subtract $2x$ from both sides.

$2x-2x-y=-2x+5$

$-y=-2x+5$

Multiply both sides by $(-1)$ .

$(-y)(-1)=(-2x+5)(-1)$

$y=2x-5$

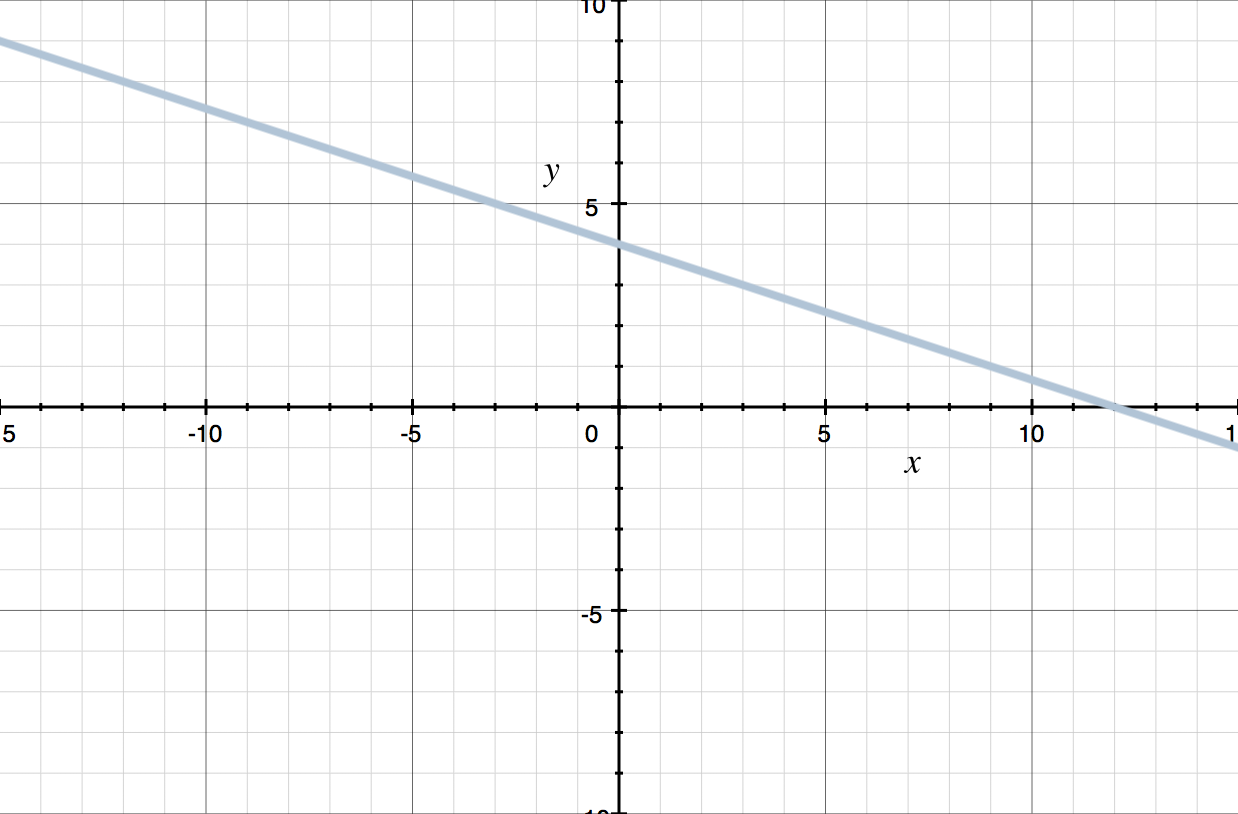
The line $y=-(1/3)x+4$ intersects the $y$ -axis at $4$ , and then has a slope of $-1/3$ , so its graph is

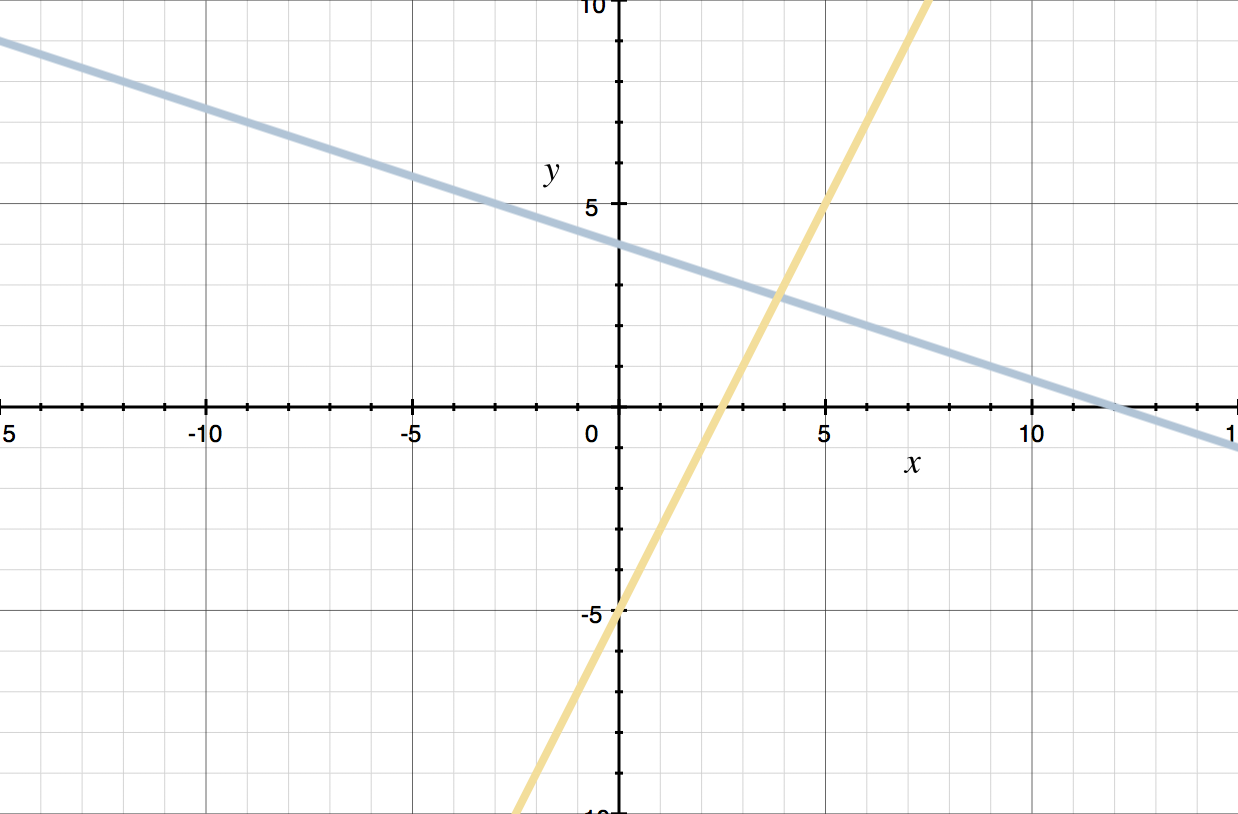
The line $y=2x-5$ intersects the $y$ -axis at $-5$ , and then has a slope of $2$ , so if you add its graph to the graph of $y=-(1/3)x+4$ , you get

graph of both lines showing their intersection point

Looking at the intersection point, it appears as though the solution is approximately $(3.75,2.75)$ . In actuality, the solution is $(27/7,19/7)\approx(3.86,2.71)$ , so our visual estimate of $(3.75,2.75)$ wasn’t that far off.