Finding the magnitude and angle of the resultant force vector
Steps for finding the magnitude and angle of a resultant force
When we’re given two vectors with the same initial point, and they’re different lengths and pointing in different directions, we can think about each of them as a force. The longer the vector, the more force it pulls in its direction.
Oftentimes we want to be able to find the net force of the two vectors, which will be a third vector that counterbalances the force and direction of the other two. Think about the resultant vector as representing the amount of force and the direction in which you’d have to pull to cancel out the force from the other two vectors.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
In order to define this third vector, we need to find
its magnitude (its length), which will be force, in Newtons N, and
its angle, from the positive direction of the ???x???-axis.
To find the magnitude and angle of a resultant force, we
create vector equations for each of the given forces
add the vector equations together to get the vector equation of the resultant force
find magnitude of the resultant force using the new vector equation and the distance formula
???D=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}???
find the angle of the resultant force using the new vector equation and the formula
???\theta_R=180^\circ-\arctan{\frac{|y|}{|x|}}???
Finding the magnitude and angle of a resultant force vector from two force vectors
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
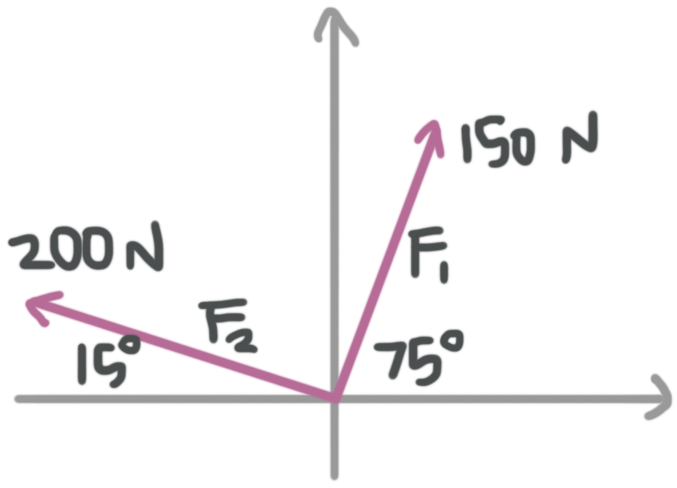
Force vectors in the first and second quadrants
Example
Find the magnitude and angle of the resultant force.
We’ll use the forces and the angles to find vector equations for ???F_1??? and ???F_2???.
???F_1=150\cos{75^\circ}\ \bold i+150\sin{75^\circ}\ \bold j???
???F_1=38.82\ \bold i+144.89\ \bold j???
???F_1=\langle38.82,\ 144.89\rangle???
and
???F_2=-200\cos{15^\circ}\ \bold i+200\sin{15^\circ}\ \bold j???
???F_2=-193.19\ \bold i+51.76\ \bold j???
???F_2=\langle-193.19,\ 51.76\rangle???
The longer the vector, the more force it pulls in its direction.
We’ll add our forces together to find the vector equation of the resultant force.
???F_R=F_1+F_2???
???F_R=38.82\ \bold i+144.89\ \bold j-193.19\ \bold i+51.76\ \bold j???
???F_R=-154.37\ \bold i+196.65\ \bold j???
???F_R=\langle-154.37,\ 196.65\rangle???
Now we can plug the vector equation into the distance formula to find the length of the resultant force vector. Because both ???F_1??? and ???F_2??? have their initial point at the origin, ???(x_1,\ y_1)??? will be ???(0,0)???.
???D_R=\sqrt{\left(x_2-0\right)^2+\left(y_2-0\right)^2}???
???D_R=\sqrt{(-154.37-0)^2+(196.65-0)^2}???
???D_R=\sqrt{23,830.10+38,671.22}???
???D_R=250.00???
To find the angle of the resultant force, we’ll use the formula
???\theta_R=180^\circ-\arctan{\frac{|y|}{|x|}}???
where ???F_R=\langle{x},y\rangle???. Plugging in ???x??? and ???y??? from the resultant force, we get
???\theta_R=180^\circ-\arctan{\frac{196.65}{154.37}}???
???\theta_R=180^\circ-51.73^\circ???
???\theta_R=128.27^\circ???
The magnitude of the resultant force is ???250??? N and the angle of the resultant force is ???128.27^\circ???.
Notice how we built the vector equations for ???F_1??? and ???F_2??? in this last example.
When we measure the angle of the vector, we always measure it from the horizontal axis, which means we’ll measure the angles of vectors in the first and fourth quadrants from the positive direction of the horizontal axis, but measure the angles of vectors in the second and third quadrants from the negative direction of the horizontal axis.
Because ???F_1??? fell in the first quadrant, we measured its angle from the positive horizontal axis as ???75^\circ???. But ???F_2??? fell in the second quadrant, which means we measured its angle from the negative direction of the horizontal axis as ???15^\circ???.
And we’ll always treat the angle between the vector and the horizontal axis as a positive angle. So even for vectors in the third and fourth quadrants, we’ll still measure a positive angle from the horizontal axis.
So, while we always keep the angles positive, we do need to change the signs of the coefficients on ???\bold i??? and ???\bold j???, depending on the quadrant of the vector. Consider a generic vector,
???F_V=F_{V_x}\cos{\theta}\ \bold i+F_{V_y}\sin{\theta}\ \bold j???
The signs we use for ???F_{V_x}??? and ???F_{V_y}??? depend on the quadrant.
In the first quadrant, ???F_{V_x}??? is positive, and ???F_{V_y}??? is positive
In the second quadrant, ???F_{V_x}??? is negative, and ???F_{V_y}??? is positive
In the third quadrant, ???F_{V_x}??? is negative, and ???F_{V_y}??? is negative
In the fourth quadrant, ???F_{V_x}??? is positive, and ???F_{V_y}??? is negative
That’s why, in the previous example, ???F_1??? in the first quadrant got two positive signs, ???F_1=150\cos{75^\circ}\ \bold i+150\sin{75^\circ}\ \bold j???, and ???F_2??? in the second quadrant got a negative sign on the first term and a positive sign on the second term, ???F_2=-200\cos{15^\circ}\ \bold i+200\sin{15^\circ}\ \bold j???.