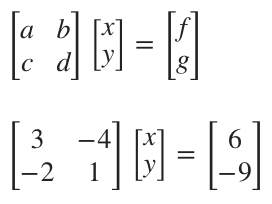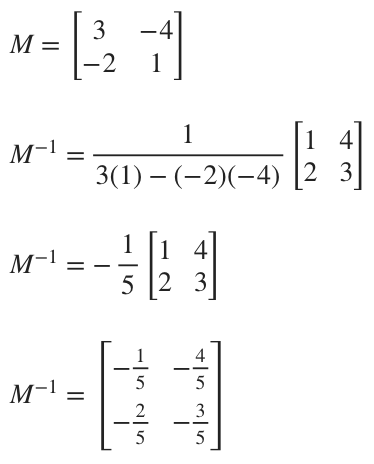Solving systems with inverse matrices
How to use matrices to solve a system of simultaneous equations
You know already how to solve systems of linear equations using substitution, elimination, and graphing. This time, we want to talk about how to solve systems using inverse matrices.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
To walk through this, let’s use a simple system.
???3x-4y=6???
???-2x+y=-9???
And for the sake of illustration, let’s compare this to the generic system
???ax+by=f???
???cx+dy=g???
You can always represent a linear system like this as the coefficient matrix, multiplied by the column vector ???(x,y)???, set equal to the column vector ???(f,g)???.
Or, if we call the coefficient matrix ???M???, rename the column vector ???(x,y)??? as ???\vec{a}???, and rename the column vector ???(f,g)??? as ???\vec{b}???, then we can say that this equation is equivalent to
???M\vec{a}=\vec{b}???
If we multiply both sides by the inverse of ???M???, ???M^{-1}???, we get
???M^{-1}M\vec{a}=M^{-1}\vec{b}???
???I\vec{a}=M^{-1}\vec{b}???
???\vec{a}=M^{-1}\vec{b}???
The reason we went through those steps to multiply by the inverse is because we now have an equation that’s solved for ???\vec{a}???, which remember is representing the column vector ???(x,y)???, which really is just the solutions to the system. In other words, this equation is saying that we can find the solutions to the system simply by multiplying the inverse matrix ???M^{-1}??? by the column vector ???(f,g)???!
Furthermore, as long as we keep ???M???, and therefore ???M^{-1}??? the same, we can substitute any values that we’d like for ???f??? and ???g??? (the constants on the right side of the system of equations), and ???\vec{a}=M^{-1}\vec{b}??? will give us an immediate solution set for ???(x,y)???.
Right now that doesn’t necessarily feel super useful, but as you use matrices in more advanced ways, it’ll become extremely valuable to be able to change the values that make up ???\vec{b}???, and immediately get the solution set for ???(x,y)??? that comes from ???\vec{a}???.
We know how to use substitution, elimination, and graphing to solve systems of equations; now we’ll use matrices
Take the course
Want to learn more about Precalculus? I have a step-by-step course for that. :)
Using the inverse matrix to solve a system of equations
Example
Use an inverse matrix to solve the system.
???3x-4y=6???
???-2x+y=-9???
Start by transferring the system into a matrix equation.
Find the inverse of the coefficient matrix.
Then we can say that the solution to the system is
Using this process with the inverse matrix, we conclude that ???x=6??? and ???y=3???.
as long as we keep M and M^(-1) the same, we can substitute any values for f and g and we’ll immediately get the solution set for (x,y).
Representing the system graphically
We can also express the same system from the example,
???3x-4y=6???
???-2x+y=-9???
as this matrix equation:
Graphically, we can think about this equation as the vector ???\vec{s}=(3,-2)??? for ???x??? and the vector ???\vec{t}=(-4,1)??? for ???y???, and the resulting vector ???\vec{u}=(6,-9)???. If we put these vectors in the same coordinate plane, we get
We already know from the example that ???x=6??? and ???y=3???. What that solution tells us graphically is that we need to put ???6??? of the ???x??? vectors ???\vec{s}=(3,-2)???, and ???3??? of the ???y??? vectors ???\vec{t}=(-4,1)??? together, and we’ll end up at the same spot as the resulting vector ???\vec{u}=(6,-9)???.